Korelācija: definīcija, nozīme un veidi statistikā
Statistikā un varbūtību teorijā korelācija nozīmē, cik cieši saistītas ir divas datu kopas.
Saikne ne vienmēr nozīmē, ka viens izraisa otru. Ļoti iespējams, ka ir iesaistīts vēl kāds trešais faktors.
Korelācijai parasti ir viens no diviem virzieniem. Tie ir pozitīvs vai negatīvs. Ja tā ir pozitīva, tad abas kopas palielinās kopā. Ja tā ir negatīva, tad viens kopums palielinās, bet otrs samazinās.
Dažādās situācijās tiek izmantoti dažādi korelācijas mērījumi. Piemēram, izkliedes grafikā cilvēki zīmē labākās atbilstības līniju, lai parādītu korelācijas virzienu.
Korelācijas jēdziens un interpretācija
Korelācijas koeficients parasti ir skaitlis, kas raksturo attiecību spēku un virzienu starp divām mainīgajām. Lielākā daļa koeficientu ir robežās no -1 līdz +1:
- +1 — pilnīga pozitīva lineāra saistība (viens mainīgais pieaug, otrs pieaug proporcionāli);
- -1 — pilnīga negatīva lineāra saistība (viens pieaug, otrs samazinās proporcionāli);
- 0 — nav lineāras saistības (var būt nelineāra sakarība vai nav sakarības).
Svarīgi atcerēties, ka skaitlis norāda tikai saistības spēku un virzienu, nevis cēloniskumu. Lai pārliecinātos par cēloņsakarību, nepieciešami kontrolēti eksperimenti vai papildu analīze (piemēram, laika secība, instrumentālie mainīgie vai piesaistīti kontroles mainīgie).
Galvenie korelācijas veidi un mērījumi
- Pīrsona korelācijas koeficients (r) — mēra lineāru saistību starp divām nepārtrauktām mainīgajām. Formula īsi: r = kov(X,Y) / (σX · σY), kur kov ir kovariācija, σ — standartnovirze. Pieņemumi inferencēm: lineāritāte, homoskedastiskums, aptuveni normāla sadalījuma paraugiem.
- Spearmana ranga korelācija (ρ) — neparametrisks mērs, kas nosaka monotonu (ne obligāti lineāru) saistību, balstoties uz mainīgo rangu vietām. Jēgpilns, ja dati nav normāli vai ir izteikti ārkārtīgi vērtības (outliers).
- Kendalla tau — vēl viena rangu metode, kas raksta sakarību kā pāru saskaņu vai nesaskaņu; bieži stabilāka mazos paraugos.
- Phi un punkt-biseriālā korelācija — izmanto bināriem vai viena bināra un viena nepārtraukta mainīgā pāriem.
Statistiskā nozīmība un uzticamība
Lai pārbaudītu, vai novērotā korelācija nav tikai gadījuma rezultāts, lieto testus un p-vērtības. Piemēram, Pīrsona r inferencēm bieži tiek izmantots t-tests ar brīvības pakāpēm n−2. Jāņem vērā izmērs (n): mazi paraugi var dot nepastāvīgus rezultātus. Tāpat ir noderīgi aprēķināt ticamības intervālu korelācijas koeficientam, lai novērtētu precizitāti.
Praktiskas piezīmes un aizsardzība pret kļūdām
- Vizualizējiet datus — pirms aprēķina skatieties izkliedes grafikus (izkliedes grafikā), jo tie atklāj nelineāras sakarības, kopējos trendus un ārējās vērtības.
- Ārkārtīgas vērtības (outliers) var būtiski mainīt Pīrsona r. Ja ir outlieri, izvēlieties Spearmana vai pārbaudiet rezultātus ar un bez šiem novērojumiem.
- Nelienātas saistības — ja sakarība ir kvadrātiska vai cita nelineāra, Pīrsona r var būt tuvu nullei, lai gan pastāv spēcīga nelineāra saistība. Tad noderēs transformācijas (log, kvadrātsakne) vai neparametriskie mēri.
- Konfūzija un mainīgie — kontrolējiet iespējamus trešos mainīgos, izmantojot daļēju (partial) korelāciju vai regresijas modeļus.
- Simpsona paradokss — kopsavilkuma līmenī var būt pretējs virziens nekā grupu līmenī; pārbaudiet sadalījumus pa apakšgrupām.
Specifiskas korelācijas formas
- Autokorelācija — laika rindās mērījums, cik novērojumi pašreizējā laikā ir saistīti ar iepriekšējiem laika punktiem; svarīgi ekonometrikā un laika rindu modelēšanā.
- Krusta korelācija — izmanto, lai novērtētu saistību starp divām signāla sekvencēm dažādos laika nobīdes posmos.
- Korelācijas matrica — lielām mainīgo grupām lieto matricu, lai redzētu pāru korelācijas; bieži attēlo ar siltuma karti (heatmap).
Kā izvēlēties pareizo rādītāju
- Ja interesē tieši lineārā saistība un pieņemumi apmierināti — Pīrsona r.
- Ja dati nav normāli, satur rangu informāciju vai ir ārkārtīgi novērojumi — Spearmana vai Kendalla.
- Ja viens vai abi mainīgie ir kategoriski — izmantojiet atbilstošus binārajiem datiem paredzētus koeficientus (phi, punkt-biseriālo).
- Ja iespējami apstākļi ar trešajiem mainīgajiem — aprēķiniet daļējo korelāciju vai veiciet multivariatīvu analīzi.
Secinājums
Korelācija ir spēcīgs rīks, lai atklātu saistības datu kopās, bet to jāizmanto piesardzīgi. Vienmēr apvienojiet kvantitatīvos rādītājus ar vizualizācijām un domājiet par iespējamiem trešajiem faktoriem vai nelineārām attiecībām. Lai izdarītu cēloņsakarīgus secinājumus, nepieciešami papildus pētījumi un piemērotas metodes.
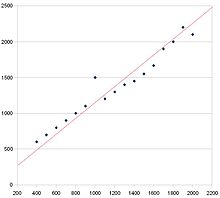
Šim izkliedes grafikam ir pozitīva korelācija. To var redzēt, jo tendence ir augšup un pa labi. Sarkanā līnija ir vislabāk atbilstīgā līnija.
Korelācijas izskaidrošana
Spēcīgs un vājš ir vārdi, ko lieto, lai raksturotu korelāciju. Ja ir spēcīga korelācija, tad visi punkti atrodas tuvu viens otram. Ja korelācija ir vāja, tad visi punkti ir izkliedēti. Ir veidi, kā ar skaitļiem parādīt, cik spēcīga ir korelācija. Šos mērījumus sauc par korelācijas koeficientiem. Vispazīstamākais no tiem ir Pīrsona korelācijas koeficients. Ievietojiet datus formulā, un tā iegūstiet skaitli. Ja šis skaitlis ir 1 vai -1, tad pastāv spēcīga korelācija. Ja atbilde ir 0, tad korelācijas nav. Cits korelācijas koeficienta veids ir Spīrmena ranga korelācijas koeficients.
Korelācija pret cēloņsakarību
Saistība ne vienmēr nozīmē, ka viena lieta izraisa otru (cēloņsakarība), jo abas lietas var būt izraisījis kas cits. Piemēram, karstās dienās cilvēki pērk saldējumu, un cilvēki dodas arī uz pludmali, kur dažus no viņiem apēd haizivis. Starp saldējuma pārdošanu un haizivju uzbrukumiem ir korelācija (šajā gadījumā, paaugstinoties temperatūrai, abi rādītāji pieaug). Taču tas, ka saldējuma pārdošanas apjomi pieaug, nenozīmē, ka saldējuma pārdošanas apjomi izraisa (cēloņsakarība) vairāk haizivju uzbrukumu vai otrādi.
Tā kā korelācija nenozīmē cēloņsakarību, zinātnieki, ekonomisti u. c. pārbaudīs savas teorijas, radot izolētu vidi, kurā tiek mainīts tikai viens faktors (ja tas ir iespējams). Tomēr politiķi, pārdevēji, ziņu aģentūras un citi cilvēki bieži iesaka, ka konkrēta korelācija nozīmē cēloņsakarību. Tas var būt saistīts ar nezināšanu vai vēlmi pārliecināt. Tādējādi ziņu reportāža var piesaistīt uzmanību, apgalvojot, ka cilvēkiem, kuri biežāk lieto kādu konkrētu produktu, ir konkrētas veselības problēmas, tādējādi norādot uz cēloņsakarību, kas patiesībā varētu būt saistīta ar ko citu.
Saistītās lapas
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Lietišķā daudzkārtējā regresijas/korelācijas analīze uzvedības zinātnēs. (3rd ed.) Hillsdale, NJ: Lawrence Erlbaum Associates.
Jautājumi un atbildes
J: Kas ir korelācija?
A: Korelācija ir veids, kā norādīt, cik cieši saistītas ir divas datu kopas.
Vai korelācija nozīmē, ka viens datu kopums izraisa otru?
A: Nē, korelācija ne vienmēr nozīmē, ka viens datu kopums izraisa otru. Patiesībā bieži vien ir iesaistīts vēl kāds trešais faktors.
Kādi ir divi korelācijas virzieni?
A: Divi korelācijas virzieni ir pozitīvs un negatīvs.
J: Ko nozīmē pozitīva korelācija?
A: Pozitīva korelācija nozīmē, ka abas datu kopas palielinās kopā.
J: Ko nozīmē negatīva korelācija?
A: Negatīva korelācija nozīmē, ka viena datu kopa palielinās, bet otra samazinās.
Vai ir dažādi korelācijas mērījumi?
A: Jā, dažādās situācijās izmanto daudz dažādu korelācijas mērījumu.
J: Kā cilvēki izkliedes grafikā bieži parāda korelācijas virzienu?
A: Lai parādītu korelācijas virzienu izkliedes grafikā, cilvēki bieži zīmē labākā pielāgojuma līniju.
