Līkņu pielāgošana: definīcija, interpolācija, izlīdzināšana, regresija
Līkņu pielāgošana: uzzini interpolāciju, izlīdzināšanu un regresiju — metodes, piemēri, ekstrapolācija un praktiski risinājumi datu modelēšanai.
Līknes pielāgošana ir matemātiskas funkcijas konstruēšana, kas vislabāk atbilst datu punktu kopumam. Mērķis var būt precīzi aprakstīt novēroto sakarību, samazināt novērojumu kļūdas ietekmi vai iegūt vienkāršu modeli turpmākai analīzei. Līknes pielāgošana var balstīties uz parametriskām pieejām (piem., lineāra vai polinoma funkcija ar konkrētiem parametriem) vai uz neparametriskām metodēm (piem., slīdošs vidējais, splaini, ģaussovska process), kur formas ierobežojums ir mazāks.
Līknes pielāgošana var ietvert interpolāciju vai izlīdzināšanu. Izmantojot interpolāciju, tiek prasīta precīza datu atbilstība — funkcija iziet caur visiem novērotajiem punktiem (piem., polinoma interpolācija vai kubiskie splaini). Izmantojot izlīdzināšanu, tiek konstruēta gluda funkcija, kas aptuveni atbilst datiem un samazina nejaušo noviržu ietekmi (piem., LOESS, kernel‑smoothing, splaini ar regulārizācijas termiņu). Saistīta tēma ir regresijas analīze, kas vairāk pievēršas statistiskās secināšanas jautājumiem — piemēram, parametru uzticamības intervāliem, hipotēžu pārbaudēm, kļūdu izkliedes novērtēšanai un modelēšanas nenoteiktībai. Reālajā darbā bieži izmanto metodes, kas apvieno interpolācijas precizitāti ar izlīdzināšanas stabilitāti, piemēram, gluduma nosacījumus ieviešot splainos vai regulārizējot polinoma koeficientus.
Pielāgotās līknes var izmantot, lai palīdzētu vizualizēt datus, uzminēt funkcijas vērtības trūkstošu datu vietā (imputācija), modelēt atkarības starp diviem vai vairākiem mainīgajiem un veikt prognozes vai kalibrācijas. Ekstrapolācija attiecas uz piemērotas līknes izmantošanu ārpus novēroto datu diapazona. Tā ir pakļauta lielākai nenoteiktībai, jo prognoze ārpus novērojumu diapazona drīzāk atspoguļo pieņemtās modeļa formas un pieņēmumus nekā faktiski novērotus datus — tāpēc pie extrapolācijas jābūt īpaši piesardzīgiem.
Biežāk lietotās metodes
- Lineārā regresija — vienkāršākais gadījums, kur sakarība starp mainīgajiem tiek modelēta ar taisnu līniju. Ļoti izplatīta, ātra un viegli interpretējama.
- Polinoma regresija — ļauj modelēt nelineāras sakarības, tomēr augsti polinomi var radīt nepastāvību (Runge fenomens).
- Splaini (piem., kubiskie splaini, B‑splaini) — saliekama pieeja, kas nodrošina lokālu kontrolu un gludu savienošanu starp daļām; labi piemēroti gan interpolācijai, gan izlīdzināšanai.
- LOESS/LOWESS — lokāla polinoma izlīdzināšana, kas labi seko lokālajām struktūrām bez globālas modeļa izveides.
- Robežās regulētas metodes (ridge, LASSO) — samazina pārlieku pielāgošanos (overfitting), īpaši, ja mainīgais skaits ir liels.
- Robusta regresija — mazina izliektu novērojumu (outliers) ietekmi, piemēram, Huber vai tukey metodes.
- Gaussovska procesa regresija — neparametriska, ļauj tieši modelēt nenoteiktību prognozēs un elastīgi pielāgot gludumu.
Interpolācija vs izlīdzināšana — ko izvēlēties?
- Ja dati tiek uzskatīti par precīziem un jums nepieciešama funkcija, kas iziet caur visiem punktiem (piem., inženierijas mērījumi bez nejaušām kļūdām), izvēlieties interpolāciju.
- Ja dati satur mērījumu kļūdas vai trokšņus, labāk izvēlēties izlīdzināšanu ar kompromisu starp atbilstību un gludumu (piem., splaini ar gluduma termiņu, LOESS).
- Izvairieties no augsta pakāpes polinoma interpolācijas, ja dati ir vienmērīgi izvietoti — tā var radīt lielas oscilācijas starp punktiem.
Modela izvēle, novērtēšana un validācija
- Novērtēšanas metrikas: reziduālu analīze, RMSE (root mean square error), MAE, R², kā arī informācijas kritēriji AIC/BIC modeļu salīdzināšanai.
- Krustošanas validācija (cross‑validation) palīdz izvēlēties gluduma parametru vai regularizācijas pakāpi un izvairīties no pārmērīgas pielāgošanās.
- Pārbaudiet reziduālu neatkarību, homoskedastiskumu un normālo sadalījumu, ja plānojat izmantot statistiskās secināšanas procedūras.
Praktiski padomi
- Stipri sakropļoti dati vai ārkārtīgi izliekti novērojumi var prasīt robustas metodes vai datu transformācijas.
- Standartizējiet mainīgos, ja izmantojat regulārizāciju vai daudzmainīgo regresiju — tas uzlabo interpretāciju un numerisko stabilitāti.
- Izmantojiet QR dekompozīciju vai SVD, lai uzlabotu skaitlisko stabilitāti lineārajās piemērošanas procedūrās.
- Vienmēr aplūkojiet grafikus: dati + pielāgotā līkne + reziduāli — vizuāla pārbaude bieži atklāj problēmas, ko neatklāj tikai skaitliski rādītāji.
Rīki un programmatūra
- R: lm(), nlme, gam, mgcv, splines pakotnes plašam metožu klāstam.
- Python: numpy, scipy.interpolate, statsmodels, scikit‑learn (regresija, regularizācija), patsciķu bibliotēkas LOESS/Gaussian process.
- MATLAB: Curve Fitting Toolbox, spline funkcijas un optimizācijas rīki.
Secinājums: līknes pielāgošana ir spēcīgs instruments datu analīzē, taču labam rezultātam nepieciešama metodes izvēle, pareiza regulēšana un rūpīga novērtēšana. Izvēloties starp interpolāciju un izlīdzināšanu, jāņem vērā datu trokšņa līmenis, mērķis (prognoze, vizualizācija, interpretācija) un nepieciešamā nenoteiktības kvantificēšana.
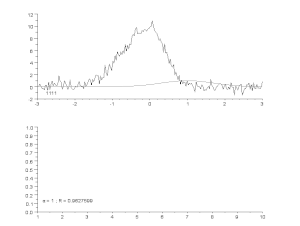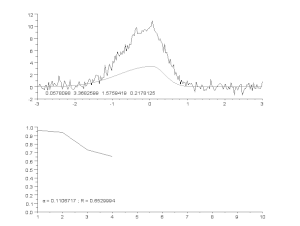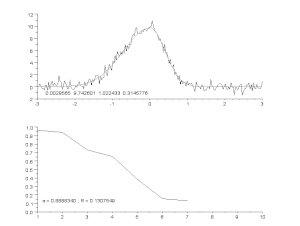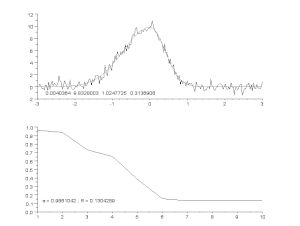
Trokšņainas līknes pielāgošana, izmantojot asimetrisku maksimuma modeli ar iteratīvu procesu (Gausa-Nūtona algoritms ar mainīgu slāpēšanas koeficientu α). Augšā: neapstrādātie dati un modelis. Apakšā: kļūdu kvadrātu normalizētās summas attīstība.
Jautājumi un atbildes
J: Kas ir līknes pielāgošana?
A.: Līknes pielāgošana ir matemātiskas funkcijas izveides process, kas vislabāk atbilst datu punktu kopumam.
J: Kādi ir divi līknes pielāgošanas veidi?
A: Divi līknes pielāgošanas veidi ir interpolācija un izlīdzināšana.
J: Kas ir interpolācija?
A: Interpolācija ir līknes pielāgošanas veids, kas prasa precīzu atbilstību datiem.
J: Kas ir izlīdzināšana?
A: Izlīdzināšana ir līknes pielāgošanas veids, kas konstruē "gludu" funkciju, kura aptuveni atbilst datiem.
J: Kas ir regresijas analīze?
A: Regresijas analīze ir radniecīga tēma, kas koncentrējas uz statistiskās secināšanas jautājumiem, piemēram, cik liela nenoteiktība pastāv līknē, kas atbilst datiem, kuri novēroti ar nejaušām kļūdām.
J: Kādi ir daži piemērotu līkņu izmantošanas veidi?
A: Pielāgotās līknes var izmantot, lai palīdzētu vizualizēt datus, uzminēt funkcijas vērtības, ja nav pieejami dati, un apkopot attiecības starp diviem vai vairākiem mainīgajiem.
J: Kas ir ekstrapolācija?
A. Ekstrapolācija ir piemērotas līknes izmantošana ārpus novēroto datu diapazona. Tomēr tā ir pakļauta zināmai nenoteiktībai, jo tā var atspoguļot līknes konstruēšanas metodi tikpat lielā mērā, cik tā atspoguļo novērotos datus.
Meklēt