Funkcija (matemātikā) — definīcija, domēns, kodomēns un piemēri
Uzzini, kas ir funkcija: skaidra definīcija, domēns, kodomēns un saprotami piemēri — ideāls resurss skolēniem un studentiem matemātikas izpratnei.
Matemātikā funkcija ir relācija starp divām kopām, kas katrai pirmās kopas (ievades) vērtībai piešķir tieši vienu otrās kopas (izvades) vērtību. Vienkāršāk — funkcija ir noteikts likums vai process, kas, saņemot ievadi, rada izvadi; izvade var būt skaitlis, vektors vai jebkura cita elementa tips kādā kopā.
Definīcija
Formāli funkciju var definēt šādi: ja X un Y ir kopas, tad f no X uz Y (rakstīts f : X → Y {\displaystyle f:X\to Y}) ir tāda daļa no karteziskā reizinājuma X×Y, ka katram x ∈ X eksistē precīzi viens y ∈ Y ar pāri (x,y) ∈ f. Šo attiecību parasti pieraksta kā y = f(x).
Domēns, kodomēns un attēls (range)
- Domēns — kopu X, kurai pieder visi pieļaujamie ievades elementi x. (Oriģināltekstā atzīmētais domēns.)
- Kodomēns — kopu Y, kurā funkcija teorētiski var dot izvades vērtības; to sauc arī par mērķkopa vai kopdomēnu. (Oriģināltekstā šī sai saite ir domēna vietā — to saprot kā kodomēnu.)
- Attēls (range) — pats par sevi ir kodomēna apakškopa: visi tie y ∈ Y, kuri patiesi tiek sasniegti kā f(x) kāda x ∈ X. Attēlu dažkārt sauc par funkcijas vērtību kopu.
Ja y ir x funkcija, raksta y = f(x), kur f apzīmē funkciju. Bieži lietotā notācija ir f : X → Y {\displaystyle f:X\to Y} — šī pieraksta ilustrācija reizēm tiek attēlota arī kā diagramma ar bultiņām, kur viena kopa (domēns) savienota ar otru (kodomēns) caur pārojumiem. 
Funkcijas piemēri
Vienkāršs piemērs: f(x) = x + 1. Ja ievades kopai izvēlamies naturālos skaitļus {0,1,2,3,...}, tad f pārvērš tos par {1,2,3,4,...}. Šajā gadījumā domēns var būt naturālo skaitļu kopa, kodomēns var būt, piemēram, naturālo skaitļu kopa vai visu veselo skaitļu kopa, bet funkcijas attēls būs tieši naturālo skaitļu kopa bez nulles. Oriģinālā piemērā izmantotie attēli un simboli apzīmē tieši šo procesu (x → y = x + 1). 
Vēl daži tipiski piemēri:
- f : R → R, f(x) = x^2 — domēns R (visi reālie skaitļi), kodomēns var būt R, bet attēls ir [0, ∞) jo kvadrāts ir nekad negatīvs.
- g : R \ {0} → R, g(x) = 1/x — domēns ir visi reālie skaitļi, izņemot 0 (jo dalīšana ar 0 nav definēta); tas parāda domēna ierobežojumu.
- Funkcija var būt arī tabula, grafiks vai algoritms — galvenais, ka katram domēna elementam ir tieši viena sasaistītā vērtība.
Attēlojuma veidi
Funkcijas var attēlot dažādos veidos:
- Formula (piem., f(x) = x + 1).
- Tabula ar pāriem (x, f(x)).
- Grafiski kartēta uz koordinātu plaknes (parasti reālām funkcijām f : R → R).
- Algoritmiski vai programmatiski — procedūra, kas aprēķina izvadi no ievades.
Īpašības: injektīva, surjektīva, bijektīva
- Injektīva (viennozīmīga) — ja dažādiem x domēnā atbilst dažādi y. Piemērs: f(x) = 2x uz R ir injektīva.
- Surjektīva (pārklāj) — ja katrs kodomēna elements ir kāda domēna elementa attēls (attēls = kodomēns). Piemērs: f : R → R, f(x) = x ir surjektīva.
- Bijektīva — ja funkcija ir gan injektīva, gan surjektīva; tad tai eksistē inversā funkcija f^{-1}.
Kompozīcija un inversā funkcija
Ja f : X → Y un g : Y → Z, tad kompozīcija g ◦ f ir funkcija no X uz Z, definēta kā (g ◦ f)(x) = g(f(x)). Inversā funkcija f^{-1} pastāv tikai tad, ja f ir bijektīva; tai ir īpašība f^{-1}(f(x)) = x visiem x domēnā.
Papildu jēdzieni
- Attēls no A: ja A ⊆ X, tad f(A) = { f(a) | a ∈ A } — attēls jeb image no kopas A.
- Preimage (priekšattēls): f^{-1}(B) = { x ∈ X | f(x) ∈ B } — kopas B priekšattēls domēnā.
- Funkcija kā relācija: matemātiski funkciju definē kā īpašu relāciju f ⊆ X×Y ar viennozīmības īpašību (katram x tieši viens y).
- Ne-funkcijas: ja kādam x atbilst vairāk nekā viens y (vai nav neviena y), tad tā nav funkcija (var saukt par daudzzīmīgu attēlojumu vai daļēju attēlojumu).
Ierobežojumi domēnā
Dažkārt domēns ir ierobežots ar kaut kādām prasībām: piemēram, kvadrātsaknes funkcijai f(x) = √x domēns reālajā kontekstā ir x ≥ 0; dalīšanas gadījumos x nedrīkst būt tāds, ka dalīšana rada nenoteiktību (dalītājs ≠ 0). Tāpēc, nosakot funkciju, jānorāda, kāda ir domēna un kodomēna definīcija.
Kopsavilkums
Funkcija ir pamatjēdziens matemātikā, kas sasaista ievades un izvades elementus caur noteiktu likumu vai relāciju. Svarīgi saprast atšķirību starp domēnu, kodomēnu un attēlu, kā arī funkcijas īpašības (injektivitāte, surjektivitāte, bijektivitāte), jo tās nosaka, vai funkcijai pastāv inversā, vai tā „aizklāj” mērķkopu utt. Funkcija nav obligāti vienkāršs vienādojums — tā var būt jebkura viennozīmīga sasaistīšana starp kopām, pat ja process ir sarežģīts vai algoritmisks.
Metaforas
Tabulas
Ieejas un izejas datus var ievietot tabulā, kā attēlā; tas ir vienkārši, ja nav pārāk daudz datu.
Grafiki
Attēlā redzams, ka gan 2, gan 3 ir savienoti pārī ar c; pretējā virzienā tas nav atļauts, 2 nevarēja izvadīt c un d,katrai ievadei var būt tikai viena izeja. Visi f ( x ) {\displaystyle f(x)} 
(c un d attēlā) parasti sauc par f attēlu kopu {\displaystyle f}
, un attēlu kopa var būt visa kodomēna vai ne. Var teikt, ka kopas A apakškopa ar attēlu kopu ir f(A). Ja ieejas un izejas ir sakārtotas, tās ir viegli uzzīmēt grafikā: 
Tādējādi attēls nonāk uz kopas A attēla. Tas padarīs gan 2, gan 3 ir pārī ar nav atļauts citā virzienā,pat var veikt starp koddomēnu vai ne. Var izdarīt secinājumu, ka kopas A apakškopa A ir attēlu kopa F(A).
Vēsture
1690. gados GotfrīdsLeibnics un Johans Bernuili lietoja vārdu funkcija ar burtiem starp tiem, tāpēc mūsdienu jēdziens radās vienlaikus ar kalkulu.
1748. gadā Leonhards Eulers sniedza: "Ja daži lielumi ir tik atkarīgi no citiem lielumiem, ka, mainot pēdējos, mainās arī pirmie, tad pirmos lielumus sauc par pēdējo funkcijām. 1755. gadā Eulergs Eulergs formulēja: "Ja daži lielumi ir tik atkarīgi no citiem lielumiem, ka, mainot pēdējos, mainās arī pirmie, tad pirmos sauc par pēdējo funkcijām. Šī definīcija ir diezgan plaši piemērojama un ietver visus veidus, kā viens lielums varētu būt atkarīgs no otra. Tātad, ja x apzīmē mainīgu lielumu, tad visus lielumus, kas jebkādā veidā ir atkarīgi no x vai ko nosaka x, sauc par x funkcijām." Tas ir ļoti mūsdienīgi.
Parasti Dirišletam piedēvē versiju, kas skolās tika izmantota līdz 20. gadsimta otrajai pusei: "y ir mainīgā x funkcija, kas definēta intervālā a < x < b, ja katrai mainīgā x vērtībai šajā intervālā atbilst noteikta mainīgā y vērtība." Tāpat nav svarīgi, kādā veidā šī atbilstība tiek noteikta.
1939. gadā Burbaki vispārināja Dirišleta definīciju un sniedza definīcijas kopu teorētisko versiju kā atbilstību starp ieejām un izejām; to sāka izmantot skolās aptuveni no 1960. gada.
Visbeidzot 1970. gadā Burbaki sniedza mūsdienu definīciju kā trijkāršu f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} 
ar F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\displaystyle F\apakškopa X\reiz Y,(x,f(x))\in F}
(t. i., f : X → Y {\displaystyle f:X\uz Y} un F = { ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } {\displaystyle F=\{{(x,f(x))|x\in X,f(x)\in Y\}}} 
).
Funkciju veidi
- Elementārās funkcijas - funkcijas, ko parasti apgūst skolā: frakcijas, kvadrātsaknes, sinusa, kosinusa un tangensa funkcijas un dažas citas funkcijas.
- Neelementāras funkcijas - Lielākajā daļā no tām netiek izmantotas darbības, kuras mēs nemācāmies skolā (piemēram, + vai -, vai pilnvaras). Daudzi integrāļi nav elementārie.
- Inversās funkcijas - funkcijas, kas atceļ citu funkciju. Piemēram: ja F(x) ir apgrieztā funkcija f(x)=y, tad F(y)=x. Ne visām funkcijām ir apgrieztās funkcijas.
- Īpašas funkcijas: Funkcijas, kurām ir nosaukumi. Piemēram: sinuss, kosinuss un tangenss. Tādas funkcijas kā f(x)=3x (trīs reizes x) netiek sauktas par speciālajām funkcijām. Tās var būt elementāras, neelementāras vai apgrieztās funkcijas.
Jautājumi un atbildes
J: Kas ir funkcija matemātikā?
Atbilde: Matemātikā funkcija ir objekts, kas, saņemot ievadi, rada izvades rezultātu, kas var būt skaitlis, vektors vai jebkas cits, kas var pastāvēt kopas iekšienē.
J: Kādas divas kopas ir saistītas ar funkcijām?
A: Visu vērtību kopu, ko var iegūt x, sauc par domēnu, un kopu, kurā ir visas vērtības, ko var iegūt y, sauc par domēnu.
J: Kā bieži apzīmē funkcijas?
A: Funkcijas bieži apzīmē ar slīpajiem burtiem, piemēram, f, g, h.
J: Kā mēs atveidojam funkciju?
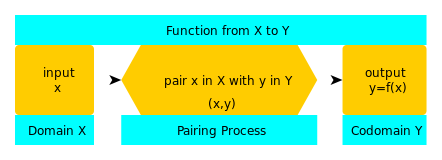
A: Funkciju attēlo, rakstot y = f(x), kur f ir funkcijas nosaukums un rakstot f : X → Y (funkcija no X uz Y), lai attēlotu trīs funkcijas daļas - domēnu (X), kopdomēnu (Y) un pāra procesu (bultiņa).
J: Vai jūs varat minēt kādas funkcijas piemēru?
A: Funkcijas piemērs ir f(x) = x + 1. Kā ievade tiek dots dabiskais skaitlis x, un tiek iegūts dabiskais skaitlis y, kas ir x + 1. Piemēram, ievadot 3 kā ieejas skaitli f, kā izejas skaitli iegūst 4.
Vai katrai funkcijai ir jābūt vienādojumam?
A: Nē, ne katrai funkcijai ir jābūt vienādojumam. Galvenā funkciju ideja ir tāda, ka ieejas un izejas ir kaut kādā veidā savienotas pa pāriem - pat ja tas var būt ļoti sarežģīti.
Meklēt