Matemātika — definīcija, pamatjēdzieni un pielietojumi

Uzzini matemātikas definīciju, pamatjēdzienus un praktiskos pielietojumus — skaitļi, struktūra, ģeometrija un analīze ikdienas un profesionālajās situācijās.

Autors: Leandro Alegsa

02-01-2026 22:19

Matemātika ir skaitļu, formu un rakstu mācība. Vārds cēlies no grieķu vārda "μάθημα" (máthema), kas nozīmē "zinātne, zināšanas vai mācība", un dažkārt tiek saīsināts līdz maths (Anglijā, Austrālijā, Īrijā un Jaunzēlandē) vai math (ASV un Kanādā). Skolēni un viņu skolas šos īsos vārdus bieži lieto ar aritmētikas, ģeometrijas vai vienkāršas algebras apzīmējumiem.

Matemātika ietver:

Skaitļi: kā lietas var saskaitīt.
Struktūra: kā lietas ir organizētas. Šo apakšnozari parasti sauc par algebru.
Vieta: vieta, kur atrodas lietas, un to izvietojums. Šo apakšnozari parasti sauc par ģeometriju.
Pārmaiņas: kā lietas kļūst citādākas. Šo apakšnozari parasti sauc par analīzi.

Matemātika ir noderīga reālajā pasaulē sastopamu problēmu risināšanā, tāpēc daudzi cilvēki, izņemot matemātiķus, studē un izmanto matemātiku. Mūsdienās matemātika ir nepieciešama daudzās profesijās. Cilvēkiem, kas strādā uzņēmējdarbībā, zinātnē, inženierzinātnēs un būvniecībā, ir nepieciešamas zināmas matemātikas zināšanas.

Pamatjēdzieni

Daži no galvenajiem matemātikas pamatjēdzieniem ir:

Skaitļi un operācijas — veseli skaitļi, racionāli un reālie skaitļi; darbības kā saskaitīšana, atņemšana, reizināšana un dalīšana. Piemērs: 2 + 2 = 4.
Kopa — objekti, kas tiek grupēti kopā pēc kāda kritērija; no kopu teorijas veidojas daudz citu matemātikas nozaru pamatā.
Funkcija — likums, kas katrai ievadei piešķir vienu iznākumu; svarīgs jēdziens analīzē un lietojumos.
Mainīgais un vienādojums — mainīgie (piemēram, x, y) un vienādojumi, kas apraksta attiecības starp tiem; tos risina, lai atrastu nezināmās vērtības.
Pierādījums — loģiska secība, kas parāda, ka apgalvojums ir patiesība, balstoties uz aksiomām un iepriekš pierādītām patiesībām.

Galvenās matemātikas nozares

Algebra — pēta simboliskās attiecības un struktūras; izmanto formulas un vienādojumus, lai modelētu situācijas.
Ģeometrija — pēta figūru formu, izmēru un īpašības; praktiski piemēri: laukumu un tilpumu aprēķini.
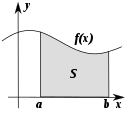
Analīze (kalkuluss) — pēta pārmaiņas un kustību; centrālie jēdzieni ir atvasinājums un integrālis. Vienkāršs piemērs: ātrums ir ceļa atvasinājums pēc laika.
Varbūtību teorija un statistika — analizē nejaušus notikumus un datus; lieto lēmumu pieņemšanā, pētījumos un kvalitātes kontrolē.
Diskrētā matemātika — pēta atsevišķus, nedalāmus objektus; svarīga datorzinātnē (grafi, kombinatorika).
Loģika un teorija pierādījumu — pētī pareizas domāšanas noteikumus un formālu secināšanu.

Pielietojumi ikdienā un darbā

Matemātiku izmanto daudzu jomu problēmu risināšanā. Daži piemēri:

Finanses un uzņēmējdarbība: procenti, procentu aprēķini, budžeta plānošana, risku novērtēšana.
Inženierzinātnes un būvniecība: konstrukciju izturības aprēķini, materiālu kvantificēšana, dizaina optimizācija.
Tehnoloģijas un datorzinātnes: algoritmi, kriptogrāfija, datu struktūras, mašīnmācīšanās modeļi.
Zinātne un medicīna: eksperimentu analīze, statistiskā secināšana, attēlu apstrāde un modelēšana.
Dienas situācijas: iepirkšanās ar atlaidēm, receptes pielāgošana, laika plānošana un maršrutu optimizācija.

Kāpēc matemātika ir svarīga

Matemātika attīsta prasmi domāt loģiski, precīzi formulēt problēmas un meklēt sistemātiskus risinājumus. Tā nodrošina instrumentus, kas ļauj modelēt un prognozēt reālās pasaules procesus. Pat ja darbā netiek lietotas sarežģītas teorijas, pamatprasmes — rēķināšana, analītiska domāšana un datu interpretācija — ir plaši pieprasītas.

Kā efektīvi mācīties matemātiku

Treniņš: regulāra uzdevumu risināšana nostiprina prasmes.
Izpratne, ne tikai mehānisms: centieties saprast, kāpēc formulas strādā.
Izmantojiet vizuālos rīkus: diagrammas, zīmējumi un grafiki palīdz saprast abstraktas idejas.
Meklējiet piemērus no reālās dzīves — tas motivē un parāda praktisku pielietojumu.
Nebaidieties uzdot jautājumus un meklēt papildu paskaidrojumus vai citus skaidrojumus, ja kāds jēdziens nešķiet skaidrs.

Īss vēsturiskais pārskats

Matemātika attīstījās tūkstošiem gadu — sākot no skaitīšanas un ģeometriskām zināšanām senajās civilizācijās (piem., Babilonijā un Ēģiptē), līdz pieaugumam klasiskajā Grieķijā, kur attīstījās aksiomatiskā domāšana. Vēlāk būtiski soļi bija kalkulusa izveide 17. gadsimtā (Isaacs Ņūtons un Gottfrīds Leibnics) un modernās matemātikas attīstība 19.–20. gadsimtā. Mūsdienās matemātika ir gan teorētiska, gan ļoti lietišķa disciplīna, kas turpina ietekmēt tehnoloģijas un zinātni.

Ja vēlaties, varu papildināt rakstu ar konkrētiem piemēriem, uzdevumiem vai attēliem, kas palīdz izprast kādu no minētajām nozarēm.

Problēmu risināšana matemātikā

Matemātika risina problēmas, izmantojot loģiku. Viens no galvenajiem loģikas instrumentiem, ko izmanto matemātiķi, ir dedukcija. Dedukcija ir īpašs domāšanas veids, lai atklātu un pierādītu jaunas patiesības, izmantojot vecas patiesības. Matemātiķim iemesls, kāpēc kaut kas ir patiess (ko sauc par pierādījumu), ir tikpat svarīgs kā fakts, ka tas ir patiess, un šo iemeslu bieži vien atrod, izmantojot dedukciju. Tieši dedukcijas izmantošana atšķir matemātisko domāšanu no citiem zinātniskās domāšanas veidiem, kas var balstīties uz eksperimentiem vai intervijām.

Matemātiķi izmanto loģiku un argumentāciju, lai izveidotu vispārīgus noteikumus, kas ir svarīga matemātikas sastāvdaļa. Šajos noteikumos nav iekļauta informācija, kas nav svarīga, lai viens noteikums varētu aptvert daudzas situācijas. Atrodot vispārīgus noteikumus, matemātiķi vienlaikus atrisina daudzas problēmas, jo šos noteikumus var izmantot citām problēmām. Šos noteikumus var saukt par teorēmām (ja tie ir pierādīti) vai pieņēmumiem (ja vēl nav zināms, vai tie ir patiesi). Lielākā daļa matemātiķu izmanto ne loģisku un radošu domāšanu, lai atrastu loģisku pierādījumu.

Dažkārt matemātika atrod un pēta noteikumus vai idejas, kuras mēs vēl nesaprotam. Bieži vien matemātikā idejas un noteikumi tiek izvēlēti tāpēc, ka tie tiek uzskatīti par vienkāršiem vai glītiem. No otras puses, dažkārt šīs idejas un noteikumi tiek atrasti reālajā pasaulē pēc tam, kad tie ir izpētīti matemātikā; tas ir noticis daudz reižu pagātnē. Kopumā matemātikas noteikumu un ideju studēšana var palīdzēt mums labāk izprast pasauli. Daži matemātikas problēmu piemēri ir saskaitīšana, atņemšana, reizināšana, dalīšana, rēķināšana, daļskaitļi un decimāldaļas. Algebras problēmas tiek risinātas, novērtējot noteiktus mainīgos lielumus. Kalkulators atbild uz visām matemātikas problēmām ar četrām aritmētiskajām pamatdarbībām.

Studiju jomas matemātikā

Numurs

Matemātika ir zinātnes nozare, kas nodarbojas ar formas, daudzuma un izkārtojuma loģiku.Matemātika ir skaitļu un daudzumu pētniecība. Lielākā daļa no turpmāk uzskaitītajām jomām tiek pētītas daudzās dažādās matemātikas jomās, tostarp kopu teorijā un matemātiskajā loģikā. Skaitļu teorijas pētījumi parasti vairāk koncentrējas uz veselu skaitļu struktūru un uzvedību, nevis uz pašu skaitļu faktiskajiem pamatiem, tāpēc šajā apakšiedaļā tie nav uzskaitīti.

0 , 1 , 1 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , 1 , ... {\displaystyle \ldots , -1,0,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0,125 , ... {\displaystyle {\frac {1}{2}},{\frac {2}{3}},0,125,\ldots } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Dabiskie skaitļi	Veseli skaitļi	Racionālie skaitļi	Reālie skaitļi	Kompleksie skaitļi
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,\div } $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}}} $f(x)={\sqrt {x}}$
Kārtējie skaitļi	Kardināli skaitļi	Aritmētiskās darbības	Aritmētiskās attiecības	Funkcijas

Struktūra

Daudzās matemātikas jomās tiek pētīta objekta struktūra. Lielākā daļa no šīm jomām ir daļa no algebras.


Skaitļu teorija	Abstraktā algebra	Lineārā algebra	Kārtības teorija	Grafu teorija

Forma

Dažās matemātikas jomās tiek pētītas lietu formas. Lielākā daļa šo jomu ir daļa no ģeometrijas.


Topoloģija	Ģeometrija	Trigonometrija	Diferenciālā ģeometrija	Fraktālā ģeometrija

Mainīt

Dažās matemātikas jomās tiek pētīts, kā lietas mainās. Lielākā daļa no šīm jomām ir daļa no analīzes.


Calculus	Vektoru aprēķins	Analīze

Diferenciālvienādojumi	Dinamiskās sistēmas	Haosa teorija

Lietišķā matemātika

Lietišķajā matemātikā matemātika tiek izmantota, lai risinātu citu jomu, piemēram, inženierzinātņu, fizikas un skaitļošanas, problēmas.

Skaitliskā analīze - optimizācija - varbūtību teorija - statistika - matemātiskās finanses - spēļu teorija - matemātiskā fizika - šķidrumu dinamika - skaitļošanas algoritmi

Slavenas teorēmas

Šīs teorēmas ir interesējušas gan matemātiķus, gan cilvēkus, kas nav matemātiķi.

Pitagora teorēma - Fermāta pēdējā teorēma - Goldbaha hipotēze - Twin Prime hipotēze - Gēdela nepabeigtības teorēmas - Puankarē hipotēze - Kantora diagonālais arguments - Četru krāsu teorēma - Zorna lema - Eulera identitāte - Baznīcas-Tūringa tēze

Tās ir teorēmas un pieņēmumi, kas ir būtiski mainījuši matemātiku.

Rīmana hipotēze - Nepārtrauktības hipotēze - P pret NP - Pitagora teorēma - Centrālā limita teorēma - Aprēķinu fundamentālā teorēma - Algebras fundamentālā teorēma - Aritmētikas fundamentālā teorēma - Projektīvās ģeometrijas fundamentālā teorēma - Virsmu klasifikācijas teorēmas - Gausa-Bonē teorēma - Fermā pēdējā teorēma - Kantoroviča teorēma

Pamati un metodes

Progress matemātikas būtības izpratnē ietekmē arī to, kā matemātiķi apgūst savu priekšmetu.

Matemātikas filozofija - Matemātiskais intuicionisms - Matemātiskais konstruktīvisms - Matemātikas pamati - Datu kopu teorija - Simboliskā loģika - Modeļu teorija - Kategoriju teorija - Loģika - Reversā matemātika - Matemātisko simbolu tabula

Vēsture un matemātiķu pasaule

Matemātika vēsturē un matemātikas vēsture.

Matemātikas vēsture - Matemātikas laika līnija - Matemātiķi - Fīldsa medaļa - Ābela balva - Tūkstošgades balvas problēmas (Māla matemātikasbalva) - Starptautiskā matemātikas savienība - Matemātikas sacensības - Laterālā domāšana - Matemātika un dzimums

Apbalvojumi matemātikā

Nav Nobela prēmijas matemātikā. Matemātiķi var saņemt Ābela balvu un Fīldsa medaļu par nozīmīgiem darbiem.

Māla matemātikas institūts ir paziņojis, ka piešķirs vienu miljonu dolāru ikvienam, kurš atrisinās kādu no Tūkstošgades balvas problēmām.

Matemātiskie rīki

Ir daudz rīku, ko izmanto, lai veiktu matemātikas uzdevumus vai atrastu atbildes uz matemātikas problēmām.

Vecāki rīki

Abacus
Napjē kauli, slaidu likums
Lineāls un kompass
Mentālais aprēķins

Jaunāki rīki

Kalkulatori un datori
Programmēšanas valodas
Datoralgebras sistēmas (uzskaitījums)
Interneta saīsinājums
statistiskās analīzes programmatūru (piemēram, SPSS).
SAS programmēšanas valoda
R programmēšanas valoda

Skatiet arī

Laika līnija par sievietēm matemātikā
Amerikas matemātiķu biedrība
Rūpnieciskās un lietišķās matemātikas biedrība
Matemātikas ģenealoģijas projekts
Matemātikas priekšmetu klasifikācija

Jautājumi un atbildes

J: Kas ir matemātika?

A: Matemātika ir skaitļu, figūru un rakstu mācība. Šis vārds cēlies no grieķu vārda μάθημα (máthema), kas nozīmē "zinātne, zināšanas vai mācība".

J: Kādas ir galvenās matemātikas jomas?

A: Galvenās matemātikas jomas ir skaitļi, struktūra (algebra), vieta (ģeometrija) un pārmaiņas (analīze).

J: Kā matemātika tiek izmantota reālajā pasaulē?

A: Lietišķā matemātika ir noderīga reālās pasaules problēmu risināšanā. Cilvēki, kas strādā uzņēmējdarbībā, zinātnē, inženierzinātnēs un būvniecībā, izmanto matemātiku.

J: Vai ir saīsināta vārda "matemātika" versija?

Atbilde: Jā - to var saīsināt līdz "maths" Britu Sadraudzības valstīs vai "math" Ziemeļamerikā.

J: Ko nozīmē vārds "matemātika"?

Atbilde: Vārds "matemātika" cēlies no grieķu vārda μάθημα (máthema), kas nozīmē "zinātne, zināšanas vai mācība".

J: Kāda veida problēmu risināšana ir saistīta ar lietišķo matemātiku?

A: Lietišķā matemātika ir saistīta ar reālu problēmu risināšanu, ar kurām saskaras cilvēki, kas strādā uzņēmējdarbībā, zinātnē, inženierzinātnēs un būvniecībā.

Meklēt