Četru krāsu teorēma — kāpēc kartei pietiek ar četrām krāsām
Četru krāsu teorēma: uzzini tās vēsturi, datorpierādījuma izaicinājumus un, kāpēc kartēm reizēm pietiek tikai ar četrām krāsām.
Četru krāsu teorēma ir matemātikas teorēma, kas apgalvo — jebkurā plaknē vai uz sfēras (t.i., kartē), kurā atzīmēti apgabali (bieži tās sauc par kartēm), pietiek ar ne vairāk kā četrām atšķirīgām krāsām, lai nokrāsotu katru apgabalu tā, lai katras pāra blakusesošās reģiona robeža būtu starp atšķirīgām krāsām. Diviem apgabaliem, kuriem ir kopīga robeža, nedrīkst piešķirt vienu un to pašu krāsu; ja kopīgais robežas daļas garums ir pozitīvs (t.i., tas ir robežas posms, nevis tikai kopīgs punkts), tos sauc par blakusesošiem.
Matemātiska formulēšana un saikne ar grafiem
Formāli karšu krāsošana ir ekvivalenta virsotni krāsošanai planāram grafam: ņem kartes dualo grafu, kur katram apgabalam atbilst virsotne, un virsotnes savieno ar malu tad, ja attiecīgo apgabalu robežas krustojas ar robežas posmu. Tādējādi četrkrāsu problēma kļūst par jautājumu par to, vai katram planāram grafikam var piešķirt virsotnēm četras krāsas tā, lai blakus esošas virsotnes būtu dažādas. Šī saikne ar plāniem grafiem ļauj izmantot grafteorijas rīkus un topoloģiskus argumentus.
Pierādījumu metodes — izsmelšana, neatvairāmie un reducējamie modeļi
Viena no galvenajām pieejām četru krāsu teorēmas pierādīšanā ir pierādījums ar izsmelšanu. Tā darbības princips ir: pierādīt, ka jebkuram planāram grafikam (vai kartei) jāeksistē viens no noteikta nevaramā kopuma (unavoidable set) konfigurācijām; tad katru no šīm konfigurācijām pierāda par reducējamu (reducible), t.i., ja tāda konfigurācija parādās iespējamiem pretpiemēriem, to var aizstāt ar mazāku konfigurāciju bez krāsojuma iespējas zaudēšanas. Ja visiem iespējamiem gadījumiem atrast var reducējamo konfigurāciju, tad pretpiemērs nevar pastāvēt, un teorēma ir pierādīta.
Šādu pierādījumu praktiska īstenošana bieži prasa ļoti daudz atsevišķu gadījumu pārbaudes — tieši to sauc par izsmelšanu. Daži pierādījumi izmanto neatvairāmā kopuma aprēķinu un pēc tam ar datora palīdzību pārbauda, ka katrs gadījums ir reducējams.
Vēsture īsumā
Ideja par kartes krāsošanu parādījās 19. gadsimta vidū. Pirmie mēģinājumi pierādīt teorēmu radīja gan pareizus, gan kļūdainus rezultātus. 1879. gadā A. Kempe publicēja pierādījumu, kas ilgu laiku tika uzskatīts par pareizu, bet 1890. gadā P. Heawood atrada kļūdu; Heawood vienlaikus pierādīja arī vieglāku piecu krāsu teorēmu, kas garantē, ka pietiek ar piecām krāsām un kurai ir īss, elementārs pierādījums.
Par pirmo tik plaši apspriesto datorizēto pierādījumu uzskata Appel un Haken 1976. gada darbu, kurā tika izmantots izsmelšanas veids ar datoru pārbaudēm. Tas pārbaudīja vairākus tūkstošus konfigurāciju (gadījumu), un kopš tā laika datorizētie pierādījumi ir nostiprinājuši rezultātu. Vēlākie darbi (piem., Robertson, Sanders, Seymour un Thomas) samazināja nepieciešamo gadījumu skaitu — mūsdienās pazīstamie pierādījumi izmanto pāris simtu līdz apmēram 600–700 reducējamu konfigurāciju, un četru krāsu teorēma tiek plaši pieņemta kā pareiza.
Kāpēc ceturtā krāsa reizēm patiešām nepieciešama
Daudzas vienkāršākas kartes var izkrāsot ar trim krāsām, taču ir konfigurācijas, kurām trīs krāsas neatbilst. Īsts piemērs ir situācija, kur viens reģions tiek ieskauts ar nepāra skaitu citu reģionu, kas savukārt veido ciklu un viens otram pieskaras (robežas posmu dalīšanās). Šādā konfigurācijā trīs krāsas neļauj izvairīties no situācijas, kur kādām divām blakus esošām teritorijām būs vienāda krāsa, tāpēc nepieciešama ceturtā krāsa. Viens šāds piemērs ir attēlā.
Nozīme un mūsdienu stāvoklis
Lai gan problēma sākotnēji bija saistīta ar valstu politisko karšu krāsošanu, praktiskā kartogrāfijā četras krāsas reti ir nepieciešamas — daudzas karšu ilustrācijas var tikt risinātas ar trīs krāsām vai ar citiem vizuālajiem paņēmieniem. Kā uzsver matemātikas vēsturnieki, četrkrāsu īpašība kartogrāfijas literatūrā bieži netiek īpaši izcelta: kartes, kurās tieši jāizmanto četras krāsas, ir retas.
Matemātiskā nozīme tomēr ir liela: četru krāsu teorēma parāda, cik sarežģīti var būt, šķietami vienkāršs, plaši saprotams jautājums, un tā mudināja attīstīt jaunus rīkus grafteorijā, datorzinātnē (automātiskai pārbaudei un certifikācijai) un kombinatorikā. Diskusijas par datoru lomu matemātikā (jo īpaši par pierādījumiem, kuri daļēji atkarīgi no datorizētām pārbaudēm) padarīja šo rezultātu arī filozofiski interesantu.
Papildus resursi
- Piecu krāsu teorēma: īss, vienkāršs pierādījums, kas parāda, ka pietiek ar piecām krāsām (sk.).
- Par datorizētajiem pierādījumiem un vēsturi lasāms vairāk matemātikas vēstures un grafteorijas literatūrā (piem., Wilson 2002).
- Ja interesē tehniskā puse, meklējiet terminus «unavoidable set» un «reducible configuration» planāro grafu kontekstā.

Ar trim krāsām nepietiek, lai šo karti nokrāsotu.

Četru krāsu kartes piemērs
Problēmas precīzs formulējums
Intuitīvi četru krāsu teorēmu var formulēt šādi: "ja plakne ir sadalīta jebkurā apgabalā, ko sauc par karti, apgabalus var iekrāsot, izmantojot ne vairāk kā četras krāsas, lai nevienam no diviem blakus esošiem apgabaliem nebūtu vienas krāsas". Lai varētu pareizi atrisināt šo uzdevumu, ir jānoskaidro daži aspekti: Pirmkārt, visi punkti, kas pieder trim vai vairāk valstīm, ir jāignorē. Otrkārt, dīvainajām kartēm ar galīga laukuma un bezgalīga perimetra reģioniem var būt vajadzīgas vairāk nekā četras krāsas.
Teorēmas nolūkiem katrai "valstij" ir jābūt vienkārši savienotam reģionam jeb pieguļošam reģionam. Reālajā pasaulē tā nav taisnība: Amerikas Savienoto Valstu sastāvā esošā Aļaska, Azerbaidžānas sastāvā esošā Nahčivana un Krievijas sastāvā esošā Kaļiņingrada nav blakusesošas valstis. Tā kā konkrētas valsts teritorijai jābūt vienas krāsas, ar četrām krāsām var nepietikt. Piemēram, aplūkojiet vienkāršotu karti, piemēram, tādu, kāda parādīta kreisajā pusē: Šajā kartē abi reģioni, kas apzīmēti ar A, pieder vienai un tai pašai valstij, un tiem jābūt vienā krāsā. Šai kartei vajadzīgas piecas krāsas, jo abi A reģioni kopā robežojas ar četriem citiem reģioniem, no kuriem katrs robežojas ar visiem pārējiem. Ja A būtu tikai trīs reģioni, varētu būt vajadzīgas sešas vai vairāk krāsas. Šādā veidā ir iespējams izveidot kartes, kurām nepieciešams patvaļīgi liels krāsu skaits. Līdzīga konstrukcija ir piemērojama arī tad, ja visām ūdenstilpnēm izmanto vienu krāsu, kā tas parasti ir reālās kartēs.
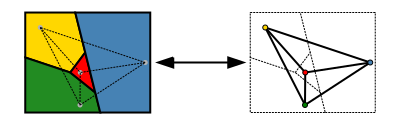
Vieglāk formulējamā teorēmas versija izmanto grafiku teoriju. Kartes reģionu kopu var attēlot abstraktāk kā nevirzītu grafiku, kurā katram reģionam ir virsotne un katram reģionu pārim, kam ir kopīgs robežposms, ir mala. Šis grafiks ir plakans: to var uzzīmēt plaknē bez krustojumiem, novietojot katru virsotni patvaļīgi izvēlētā vietā reģionā, kuram tā atbilst, un uzzīmējot malas kā līknes, kas katrā reģionā ved bez krustojumiem no virsotnes vietas uz katru kopīgo reģiona robežpunktu. Un otrādi, no kartes šādā veidā var izveidot jebkuru plakanu grafiku. Grafu teorijas terminoloģijā četru krāsu teorēma nosaka, ka katra planārā grafika virsotnes var iekrāsot ne vairāk kā četrās krāsās tā, lai nevienai no divām blakus esošajām virsotnēm nebūtu vienādas krāsas, jeb, īsāk sakot, "katrs planārais grafiks ir četrkrāsains" (Thomas 1998, 849. lpp.; Wilson 2002).

Azerbaidžānas kartes piemērs ar nesaistītiem reģioniem

Šo karti nevar iekrāsot ar četrām krāsām
Vēsture
Pirmais, kurš nosauca šo problēmu, bija Frānsiss Gatrijs 1852. gadā. Tajā laikā viņš bija jurisprudences students Anglijā. Viņš atklāja, ka Anglijas grāfistu kartes iekrāsošanai vajadzīgas vismaz četras krāsas. Augusts de Morgans pirmo reizi par šo problēmu runāja vēstulē, ko viņš 1852. gada augustā rakstīja Rovanam Hamlitonam. Vēstulē de Morgans jautā, vai ar četrām krāsām patiešām pietiek, lai iekrāsotu karti tā, ka valstis, kas atrodas viena otrai blakus, iegūst dažādas krāsas.
Angļu matemātiķis Artūrs Keilijs (Arthur Cayley) 1878. gadā ar šo problēmu iepazīstināja matemātiķu biedrību Londonā. Gada laikā Alfrēds Kempe atrada kaut ko līdzīgu problēmas pierādījumam. Vienpadsmit gadus vēlāk, 1890. gadā, Pērsijs Hīvuds pierādīja, ka Alfrēda pierādījums ir kļūdains. Pīters Gatrijs Taits 1880. gadā iesniedza vēl vienu pierādījuma mēģinājumu. Pagāja vienpadsmit gadi, lai pierādītu, ka arī Taita pierādījums nedarbojas. 1891. gadā to varēja pierādīt Jūliuss Petersens (Julius Petersen). Kad viņš falsificēja Keilija pierādījumu, Kempe parādīja arī pierādījumu problēmai, ko viņš nosauca par piecu krāsu teorēmu. Teorēma saka, ka jebkuru šādu karti var iekrāsot ne vairāk kā ar piecām krāsām. Pastāv divi ierobežojumi: Pirmkārt, jebkura valsts ir pieguļoša, tajā nav eksklavu. Otrais ierobežojums ir tāds, ka valstīm ir jābūt kopīgai robežai; ja tās tikai kādā punktā saskaras, tās var iekrāsot ar vienu krāsu. Lai gan Kempes pierādījums bija kļūdains, viņš izmantoja dažas idejas, kas vēlāk ļāva izveidot pareizu pierādījumu.
Pagājušā gadsimta 60. un 70. gados Heinrihs Hēšs (Heinrich Heesch) izstrādāja pirmo datorizēta pierādījuma skici. Kenets Appels un Volfgangs Hakens 1976. gadā šo skici uzlaboja (Robertsons u. c., 1996). Viņiem izdevās samazināt pārbaudāmo gadījumu skaitu līdz 1936 gadījumiem; vēlāk tika izveidota versija, kas paļāvās tikai uz 1476 gadījumu pārbaudi. Katrs gadījums bija jāpārbauda ar datoru (Appel & Haken 1977).
1996. gadā Nīls Robertsons, Daniels Sanderss, Pols Seimūrs un Robins Tomass uzlaboja šo metodi un samazināja pārbaudāmo gadījumu skaitu līdz 663 gadījumiem. Arī šajā gadījumā katrs gadījums bija jāpārbauda ar datoru.
2005. gadā Žoržs Gontjē un Bendžamins Verners izstrādāja formālu pierādījumu. Tas bija uzlabojums, jo pirmo reizi ļāva izmantot teorēmu pierādīšanas programmatūru. Izmantotā programmatūra saucas Coq.
Četru krāsu teorēma ir pirmā lielā matemātiskā problēma, kas tika pierādīta ar datora palīdzību. Tā kā pierādījumu nevarēja veikt cilvēks, daži matemātiķi to neatzina par pareizu. Lai pierādījumu pārbaudītu, ir jāpaļaujas uz pareizi strādājošu programmatūru un aparatūru, kas apstiprinātu pierādījumu. Tā kā pierādījums tika veikts ar datora palīdzību, tas arī nav ļoti elegants.
Mēģinājumi, kas izrādījās nepareizi
Četru krāsu teorēma ir bijusi bēdīgi slavena ar to, ka tās ilgajā pastāvēšanas vēsturē ir bijis liels skaits kļūdainu pierādījumu un atspēkojumu. Sākumā laikraksts The New York Times atteicās ziņot par Apela-Hakena pierādījumu. Laikraksts to darīja politisku apsvērumu dēļ; tas baidījās, ka pierādījums varētu izrādīties nepatiess tāpat kā iepriekšējie (Wilson 2002, 209. lpp.). Dažiem pierādījumiem bija nepieciešams ilgs laiks, līdz tos varēja viltojot: Kempes un Taita pierādījumu viltošana prasīja vairāk nekā desmit gadus.
Visvienkāršākie pretprakti parasti mēģina izveidot vienu reģionu, kas skar visus pārējos. Tas liek pārējos reģionus iekrāsot tikai ar trim krāsām. Tā kā četru krāsu teorēma ir patiesa, tas vienmēr ir iespējams; tomēr, tā kā persona, kas zīmē karti, ir koncentrējusies uz vienu lielu reģionu, tā nepamana, ka pārējos reģionus patiesībā var iekrāsot ar trim krāsām.
Šo triku var vispārināt: Ja dažu reģionu krāsas kartē ir izvēlētas iepriekš, pārējos reģionus nav iespējams iekrāsot tā, lai kopumā tiktu izmantotas tikai četras krāsas. Kāds, kas pārbauda pretpiemēru, var neiedomāties, ka var būt nepieciešams mainīt šo reģionu krāsu. Tādējādi pretparaugs izskatīsies derīgs, lai gan tas tāds nav.
Iespējams, viens no iemesliem, kas ir pamatā šim izplatītajam maldīgajam priekšstatam, ir tas, ka krāsu ierobežojums nav transitīvs: reģionam ir jābūt iekrāsotam atšķirīgi tikai no reģioniem, kuriem tas tieši pieskaras, nevis no reģioniem, kas pieskaras reģioniem, kuriem tas pieskaras. Ja šāds ierobežojums būtu spēkā, plakanu grafiem būtu nepieciešams patvaļīgi liels krāsu skaits.
Citi kļūdaini pierādījumi pārkāpj teorēmas pieņēmumus negaidītā veidā, piemēram, izmantojot reģionu, kam ir vairākas nesaistītas daļas, vai nepieļaujot, ka vienas krāsas reģioni kādā punktā pieskaras.
Politisko karšu krāsošana
Reālajā dzīvē daudzām valstīm ir eksklavi vai kolonijas. Tā kā tās pieder valstij, tām jābūt iekrāsotām tādā pašā krāsā kā mātes valstij. Tas nozīmē, ka parasti šādas kartes izkrāsošanai ir nepieciešamas vairāk nekā četras krāsas. Kad matemātiķi runā par grafiku, kas saistīts ar šo uzdevumu, viņi saka, ka tas nav plakans. Lai gan ir viegli pārbaudīt, vai grafiks ir planārs, atrast vismazāko vajadzīgo krāsu skaitu, lai to iekrāsotu, ir ļoti grūti. Tā ir NP-pilna, kas ir viena no sarežģītākajām pastāvošajām problēmām. Mazāko krāsu skaitu, kas nepieciešams, lai iekrāsotu grafiku, sauc par tā hromatisko skaitli. Daudzas problēmas, kas rodas, mēģinot atrisināt četru krāsu teorēmu, ir saistītas ar diskrēto matemātiku. Šī iemesla dēļ bieži tiek izmantotas algebriskās topoloģijas metodes.
Paplašinājums "ne-plakanām" kartēm
Četru krāsu teorēma paredz, ka "kartei" jāatrodas uz līdzenas virsmas, ko matemātiķi sauc par plakni. 1890. gadā Pērsijs Džons Hīvuds (Percy John Heawood) radīja to, ko šodien sauc par Hīvuda hipotēzi: Tā uzdod to pašu jautājumu, ko četru krāsu teorēma, bet jebkuram topoloģiskam objektam. Piemēram, torus var iekrāsot ne vairāk kā ar septiņām krāsām. Hēvuda hipotēze dod formulu, kas darbojas visiem šādiem objektiem, izņemot Kleina pudeli.
Jautājumi un atbildes
J: Kas ir četru krāsu teorēma?
A: Četru krāsu teorēma ir matemātiska teorēma, kas nosaka, ka jebkurā plaknē, kurā ir apgabali, apgabalus var iekrāsot ne vairāk kā četrās krāsās. Blakus esošie apgabali nedrīkst būt vienā krāsā.
J: Kā tika iegūts pirmais četru krāsu teorēmas pierādījums?
A.: Pirmais četru krāsu teorēmas pierādījums bija pierādījums ar izsmelšanu, kurā bija 1936 gadījumi. Tas nozīmē, ka tā tika noteikta, sadalot to gadījumos un pierādot katru gadījumu atsevišķi.
J: Vai šī problēma interesē kartogrāfus?
Atbilde: Nē, kartogrāfus šī problēma īpaši neinteresē, jo kartes, kurās izmanto tikai četras krāsas, ir reti sastopamas, un parasti tām nepieciešamas tikai trīs krāsas. Grāmatās par kartogrāfiju un karšu veidošanas vēsturi četru krāsu īpašība nav minēta.
J: Kas ir piecu krāsu teorēma?
A: Piecu krāsu teorēma nosaka, ka piecas krāsas ir pietiekamas kartes krāsošanai, un tai ir īss, elementārs pierādījums, kas tika pierādīts 19. gadsimta beigās.
Jautājums: Cik grūti bija pierādīt, ka karšu krāsošanai vajadzīgas tikai četras krāsas?
A: Pierādīt, ka karšu krāsošanai vajadzīgas tikai 4 krāsas, izrādījās daudz grūtāk, nekā gaidīts, jo kopš tās pirmā apgalvojuma 1852. gadā ir parādījušies daudzi kļūdaini pierādījumi un kļūdaini pretpierādījumi.
J: Vai ir kāds piemērs kartei, kurā būtu vajadzīgas 5 vai vairāk krāsas, lai pareizi iekrāsotu visus reģionus?
Jā, viens no šādiem piemēriem ir gadījums, kad vienu reģionu ieskauj nepāra skaits citu reģionu, kas viens otram pieskaras cikliski - šajā gadījumā var būt nepieciešamas 5 vai vairāk krāsas, lai pareizi nokrāsotu visus reģionus.
Meklēt

