Pitagora teorēma — definīcija, formula (a²+b²=c²), piemēri un pierādījumi

Pitagora teorēma — skaidra definīcija, formula a²+b²=c², saprotami piemēri un dažādi pierādījumi soli pa solim, praktiski uzdevumu risināšanas padomi.

Autors: Leandro Alegsa

22-01-2026 22:41

Pitagora teorēma jeb Pitagora likums matemātikā ir pamatapgalvojums par taisnā trīsstūra malām. Tā nosaka sakarību starp divām trijstūra kājām un hipotenūzu un ir būtiska ģeometrijā, trigonometrijā un daudzu citu nozaru pamatos.

Viens no taisnā trīsstūra leņķiem vienmēr ir vienāds ar 90 grādiem. Šis leņķis ir taisnais leņķis. Abas malas, kas atrodas blakus taisnajam leņķim, sauc par kājām, bet otru malu sauc par hipotenūzi. Hipotenūza ir pretējā puse taisnajam leņķim, un tā parasti ir garākā mala. Teorēma tradicionāli saistīta ar grieķu matemātiķi Pitagoru, pēc kura tā arī ieguvusi nosaukumu.

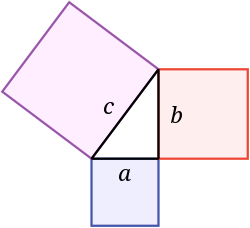
Pitagora teorēma saka, ka kvadrāta laukums uz hipotenūzas ir vienāds ar kāju kvadrātu laukumu summu. Attēlā zilā kvadrāta laukums, pieskaitot sarkanā kvadrāta laukumu, veido violetā kvadrāta laukumu. Ja kāju garumi ir a un b, un hipotenūzas garums ir c, tad a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

Pierādījumi — galvenās kategorijas

Šai teorēmai ir daudz dažādu pierādījumu. Tos parasti iedala četrās galvenajās kategorijās:

ģeometriskie pierādījumi (disekcijas un pārkārtošanas pierādījumi);
pierādījumi, kas izmanto līdzīgus trijstūrus (izmantojot leņķu līdzību un proporcijas);
algebriskie pierādījumi (izmantojot laukumu aprēķinus vai vienādojumus);
analītiskie un vektoriskie pierādījumi (izmantojot koordinātas vai vektorus).

Daži īsi pierādījumu paraugi

Reorganizēšanas pierādījums (disekcija): Uzbūvē laukumu (kvadrātu) ar malu a + b un parādi, ka tā laukums (a+b)² var tikt sadalīts kā c² plus četri mazi trijstūri ar kopējo laukumu 2ab, no kura iegūst a² + b² = c². Šāds pierādījums ir ļoti vizuāls un bieži tiek izmantots mācībās.
Nodarbošanās ar līdzīgiem trijstūriem: No taisnā trijstūra projekcijas uz hipotenūzu veido divus mazākus trijstūrus, kas abi ir līdzīgi sākotnējam. No līdzības seko attiecības a² = c·(c − a') u. tml., kur apvienojot iegūst a² + b² = c².
Analītiskais pierādījums: Novietojot taisno trijstūri tā, lai kājas atrastos uz koordinātu asīm (piem., virsotnes (0,0), (a,0), (0,b)), hipotenūzas garums pēc distanču formulas ir sqrt(a² + b²), no kuras izriet a² + b² = c².

Piemēri

Visvienkāršākais piemērs: ja a = 3 un b = 4, tad c = sqrt(3² + 4²) = sqrt(9 + 16) = sqrt(25) = 5. Tas veido pazīstamo trijstūri 3–4–5.
Vēl viens: a = 5, b = 12 → c = sqrt(25 + 144) = sqrt(169) = 13 (trijstūris 5–12–13).

Pitagora trijstūri (Pitagora tripleti)

Skaitļu trijstūri (a, b, c), kuri apmierina a² + b² = c² un kuriem a, b, c ir veseli skaitļi, sauc par Pitagora tripletiem. Tie var būt primitīvi (kad a, b, c ir savstarpēji pirmskaitļi) vai neprimīti. Visi primitīvie tripleti var tikt ģenerēti ar parametru formulu:

a = m² − n², b = 2mn, c = m² + n², kur m > n ir pozitīvi veseli, m un n ir savstarpēji pirmskaitļi un viens no tiem ir pāra, otrs nepāra.

Pitagora teorēmas konversija

Konversija: ja trīsstūris ar malām a, b, c apmierina a² + b² = c², tad šis trijstūris ir taisnais, un mala c ir hipotenūza. Konversija izriet, piemēram, no kosinusa likuma vai no izmērāmā leņķa vienkāršām īpašībām.

Lietojumi un nozīmīgums

Attālumu mērīšana un koordinātu ģeometrija (distances formula);
celtniecība, inženierija, kartēšana un ģeodēzija;
trigonometrijas pamatlikumu atvasināšana (piem., sin² + cos² = 1);
datorgrafika, robotika un fizikas problēmas, kur svarīgas attālumu un vektoru īpašības.

Vispārinājumi

Pitagora teorēma ir īpašs Kosinusa likuma gadījums, kas attiecas uz jebkuru trijstūri: c² = a² + b² − 2ab cos γ. Ja γ = 90°, tad cos γ = 0 un iegūst Pitagora likumu. Ir arī vispārinājumi uz augstākām dimensijām, piemēram, eiklīdiskā telpā punktu attālumu kvadrātu summa rodas no koordinātu kvadrātu summas.

Kopsavilkums: Pitagora teorēma ir vienkārša, bet ārkārtīgi jaudīga — tā sniedz tiešu sakarību starp taisnā trijstūra malām, ir pierādāma dažādos veidos, dod pamatu daudzām matemātikas un praktisku pielietojumu jomām un vada uz tādiem tematiem kā Pitagora tripleti un kosinusa likums.

Pierādījums

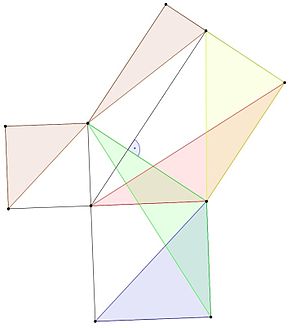
Vienu Pitagora teorēmas pierādījumu atrada grieķu matemātiķis Eudokss no Knidas.

Pierādījumā izmantotas trīs lemas:

Trīsstūriem ar vienādu pamatu un augstumu ir vienāds laukums.
Trīsstūrim, kura pamatne un augstums ir vienāds ar kvadrāta malu, ir tāds pats laukums kā kvadrāta pusei.
Trīsstūri ar divām vienādām malām un vienu vienādu leņķi ir kongruenti un tiem ir vienāds laukums.

Pierādījums ir šāds:

Zilā trijstūra laukums ir tāds pats kā zaļā trijstūra, jo tā pamatne un augstums ir vienāds (1. lemma).
Gan zaļajam, gan sarkanajam trijstūrim ir divas malas, kas vienādas ar viena un tā paša kvadrāta malām, un leņķis, kas vienāds ar taisnu leņķi (90 grādu leņķis) plus trīsstūra leņķis, tāpēc tie ir kongruenti un tiem ir vienāds laukums (3. lemma).
Sarkanā un dzeltenā trīsstūra laukumi ir vienādi, jo to augstumi un pamatnes ir vienādi (1. lemma).
Zilā trīsstūra laukums ir vienāds ar dzeltenā trīsstūra laukumu, jo

A b l u e = A g r e e n = A r e d = A y e l o w {\displaystyle {\color {blue}A_{blue}}}={\color {green}A_{green}}={\color {red}A_{red}}}={\color {yellow}A_{yellow}}}} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Brūnajiem trijstūriem ir tāda pati platība to pašu iemeslu dēļ.
Zilajam un brūnajam kvadrātam ir puse no mazāka kvadrāta laukuma. To laukumu summa ir vienāda ar pusi no lielākā kvadrāta laukuma laukuma. Tāpēc mazo kvadrātu laukumu laukumu puses ir vienādas ar lielākā kvadrāta laukuma laukuma pusi, tātad to laukumi ir vienādi ar lielākā kvadrāta laukumu.

Pierādījums, izmantojot līdzīgus trijstūrus

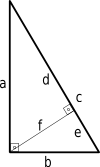
Mēs varam iegūt vēl vienu Pitagora teorēmas pierādījumu, izmantojot līdzīgus trīsstūrus.

d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\displaystyle {\frac {d}{a}}}={\frac {a}{c}}\kvadrāts \Pareizā bultiņa \kvadrāts d={\frac {a^{2}}{c}}\kvadrāts (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

No attēla redzam, ka c = d + e {\displaystyle c=d+e\,\! } $c=d+e\,\!$ . Un, aizstājot (1) un (2) vienādojumu:

c = a 2 c + b 2 c {\displaystyle c={\frac {a^{2}}}{c}}+{\frac {b^{2}}}{c}}}}} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

reizināšana ar c:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\!. } $c^{2}=a^{2}+b^{2}\,\!.$

Pitagora trijnieki

Pitagora trīsnieki jeb tripleti ir trīs veseli skaitļi, kas atbilst vienādojumam a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

Labi zināms piemērs ir trijstūris ar malām 3, 4 un 5. Ja a=3 un b=4, tad 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}} $3^{2}+4^{2}=5^{2}$ , jo 9 + 16 = 25 {\displaystyle 9+16=25} $9+16=25$ . To var parādīt arī kā 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}}=5.}. ${\sqrt {3^{2}+4^{2}}}=5.$

Trijstūris trīs-četri-piecas darbojas visiem 3, 4 un 5 reizinājumiem. Citiem vārdiem sakot, tādi skaitļi kā 6, 8, 10 vai 30, 40 un 50 arī ir Pitagora trijnieki. Vēl viens trijstūra piemērs ir trijstūris 12-5-13, jo 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}}=13}} ${\sqrt {12^{2}+5^{2}}}=13$ .

Pitagora trīskāršo, kas nav citu trīskāršo reizinājums, sauc par primitīvo Pitagora trīskāršo. Jebkuru primitīvo Pitagora trīsvienādojumu var atrast, izmantojot izteicienu ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})}}. $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , bet ir jāizpilda šādi nosacījumi. Tie ierobežo m {\displaystyle m} un n {\displaystyle n} vērtības.

m {\displaystyle m} un n {\displaystyle n} ir pozitīvi veseli skaitļi
m {\displaystyle m} un n {\displaystyle n} nav kopīgu faktoru, izņemot 1
m {\displaystyle m} un n {\displaystyle n} ir pretēja paritāte. m {\displaystyle m} un n {\displaystyle n} ir pretēja paritāte, ja m {\displaystyle m} ir pāra un n {\displaystyle n} ir nepāra vai m {\displaystyle m} ir nepāra un n {\displaystyle n} ir pāra.
m > n {\displaystyle m>n} .

Ja visi četri nosacījumi ir izpildīti, tad m {\displaystyle m} un n {\displaystyle n} vērtības veido primitīvu Pitagora trīsvienību.

m = 2 {\displaystyle m=2} $m=2$ un n = 1 {\displaystyle n=1} $n=1$ veido primitīvu Pitagora trīsvienādojumu. Vērtības atbilst visiem četriem nosacījumiem. 2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2\reiz 2\reiz 1=4}. $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ un m 2 + n 2 = 2 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ Tādējādi tiek izveidots trijnieks ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ .

Jautājumi un atbildes

J: Kas ir Pitagora teorēma?

A: Pitagora teorēma ir apgalvojums par taisnā trīsstūra malām.

J: Kāds leņķis taisnā trijstūrī vienmēr ir vienāds ar 90 grādiem?

A: Viens no taisnā trīsstūra leņķiem vienmēr ir vienāds ar 90 grādiem, un to sauc par taisno leņķi.

J: Kā sauc abas malas, kas atrodas blakus taisnajam leņķim?

A: Abas blakus taisnajam leņķim esošās malas sauc par kājām.

J: Kā sauc malu, kas atrodas pretī taisnajam leņķim?

A: Taisnajam leņķim pretējo malu sauc par hipotenūzi, un tā vienmēr ir garākā mala.

J: Vai ir kāds vienādojums šīs teorēmas aprēķināšanai?

A: Jā, ir vienādojums šīs teorēmas aprēķināšanai, kas nosaka, ka "hipotenūzas garuma kvadrāts ir vienāds ar pārējo divu malu garumu kvadrātu summu".

Vai visus trīsstūrus ar 90 grādu leņķiem uzskata par "taisniem" trīsstūriem?

A: Nē, ne visus trīsstūrus ar 90 grādu leņķiem uzskata par "taisniem" trīsstūriem; par "taisniem" trīsstūriem var uzskatīt tikai tos, kuros viena mala (hipotenūza) ir garāka par pārējām divām malām un tās galā veido 90 grādu leņķi.

Meklēt