Algoritms

Algoritmu salīdzināšana

Parasti ir vairāk nekā viens veids, kā atrisināt problēmu. Var būt daudz dažādu recepšu, kā pagatavot kādu ēdienu, kas izskatās atšķirīgi, bet galu galā garšo vienādi, kad viss ir pateikts un izdarīts. Tas pats attiecas arī uz algoritmiem. Tomēr daži no šiem veidiem būs labāki par citiem. Ja receptei nepieciešams daudz sarežģītu sastāvdaļu, kuru jums nav, tā nav tik laba kā vienkārša recepte. Kad mēs aplūkojam algoritmus kā problēmu risināšanas veidu, bieži vien mēs vēlamies zināt, cik ilgā laikā dators atrisinātu problēmu, izmantojot konkrēto algoritmu. Rakstot algoritmus, mēs vēlamies, lai mūsu algoritms aizņemtu pēc iespējas mazāk laika, lai mēs varētu atrisināt problēmu pēc iespējas ātrāk.

Dažas receptes gatavošanā ir grūtāk izpildāmas nekā citas, jo to pabeigšanai nepieciešams vairāk laika vai vairāk lietu, kurām jāseko līdzi. Tāpat ir arī ar algoritmiem, un algoritmi ir labāki, ja tos ir vieglāk izpildīt datoram. To, ar ko mēra algoritma sarežģītību, sauc par sarežģītību. Kad mēs jautājam, cik sarežģīts ir algoritms, bieži vien mēs vēlamies zināt, cik ilgā laikā dators atrisinās uzdevumu, ko vēlamies, lai tas atrisinātu.

Šķirošana

Šis ir algoritma piemērs karšu ar krāsām sakārtošanai vienas krāsas kaudzītēs:

1. Paņemiet visas kartes.
2. Izvēlieties karti no savas rokas un apskatiet tās krāsu.
3. Ja jau ir šīs krāsas kāršu kaudzīte, nolieciet šo kārti uz tās kaudzītes.
4. Ja nav šīs krāsas kāršu kaudzītes, izveidojiet jaunu kaudzīti tikai ar šīs krāsas kārtīm.
5. Ja Jūsu rokās joprojām ir karte, atgriezieties pie otrā soļa.
6. Ja Jūsu rokās vēl nav nevienas kārts, tad kārtis tiek sakārtotas. Jūs esat beidzis.

Šķirošana pēc skaitļiem

Šie ir algoritmu piemēri, kā sakārtot kāršu kaudzi ar daudziem dažādiem skaitļiem tā, lai skaitļi būtu sakārtoti.

Spēlētāji sāk ar kāršu kaudzi, kas nav sakārtotas.

Pirmais algoritms

Šis algoritms izskata kāršu kaudzi pa vienai kartei. Šī karte tiek salīdzināta ar nākamo karti kaudzē. Lūdzu, ņemiet vērā, ka šī pozīcija mainās tikai 6. solī. Šo algoritmu sauc par burbuļu šķirošanu. Tas ir lēns.

1. Ja kāršu kaudze ir tukša vai tajā ir tikai viena kārts, tā ir sakārtota un viss ir izdarīts.
2. Paņemiet kāršu kaudzīti. Paskatieties uz kaudzes pirmo kārti (augšējo).
3. Jūsu aplūkojamā karte ir karte A. Karte A pašlaik atrodas P kaudzītē.
4. Ja pēc A kārtis kaudzītē vairs nav citu kāršu, pārejiet uz 8. soli.
5. Nākamā kārts kaudzītē ir B karte.
6. Ja kartē B ir mazāks skaitlis nekā kartē A, apmainiet kāršu A un B pozīcijas. atcerieties, ka to izdarījāt. Kad apmaināsiet kārtis, nemainiet pozīciju P.
7. Ja pēc P pozīcijas kaudzītē ir vēl viena karte, paskatieties uz to; atgriezieties pie 3. soļa.
8. Ja pēdējā izspēlē neesat mainījis nevienas kārtis, tad kāršu kaudze ir sakārtota.
9. Pretējā gadījumā atgriezieties pie 2. soļa.

Soli pa solim piemērs

Paņemsim kāršu kaudzi ar skaitļiem "5 1 4 2 8" un sakārtosim to no mazākā skaitļa līdz lielākajam, izmantojot šo algoritmu. Katrā solī algoritms salīdzina treknrakstā rakstītos elementus. Kāršu kaudzes augšdaļa ir kreisajā pusē.

Pirmā eja:
( 5 1 1 4 2 8 ) → {\displaystyle \to } ( 1 5 5 4 4 2 8 ) Šeit algoritms salīdzina pirmos divus elementus un tos apmaina.
( 1 5 4 4 2 8 ) → {\displaystyle \to } ( 1 4 5 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 2 5 8 ) Šie elementi jau ir sakārtoti, tāpēc algoritms tos nemaina.
Otrais gājiens:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )(
1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 2 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 4 5 8 )
Tagad kāršu kaudze jau ir sakārtota, bet mūsu algoritms to nezina. Algoritmam ir nepieciešams viens vesels piegājiens bez jebkādas apmaiņas, lai zinātu, ka tā ir sakārtota.
Trešais gājiens:
( 1 2 4 4 5 8 ) → {\displaystyle \to } ( 1 2 4 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 2 4 5 5 8 )
Visbeidzot, masīvs ir sakārtots, un algoritms var apstāties.

Vēsture

Šis ir viegli saprotams šķirošanas algoritms. Datorzinātnieki to nosauca par burbuļveida šķirošanu, jo mazāki elementi pacelsies uz augšu, mainot savu pozīciju katrā piegājienā. Diemžēl šis algoritms nav pārāk labs, jo, lai šķirotu, ir nepieciešams ilgs laiks (daudzas ejas cauri kāršu kaudzei).

Otrais algoritms

Šis algoritms izmanto citu ideju. Dažreiz problēmas atrisināšana ir sarežģīta, bet problēmu var mainīt tā, lai to veidotu vienkāršākas problēmas, kuras ir vieglāk atrisināt. To sauc par rekursiju. Tas ir grūtāk saprotams nekā pirmais piemērs, bet tas dos labāku algoritmu.

Pamatideja

1. Ja kaudzītē nav nevienas kartes vai ir tikai viena karte, tā ir sakārtota, un Jūs esat pabeidzis.
2. Sadaliet kāršu kaudzi divās apmēram vienāda lieluma daļās. Ja kāršu skaits ir nepāra, vienā no abām kaudzītēm būs par vienu karti vairāk nekā otrā.
3. Sakārtojiet katru no abām kaudzēm, izmantojot šo algoritmu (Katrai kaudzei sāciet ar šī saraksta 1. punktu.)
4. Apvienojiet abas sakārtotās kaudzes kopā, kā aprakstīts tālāk.
5. Rezultāts ir sakārtota kāršu kaudze. Jūs esat pabeidzis.

Divu kaudžu apvienošana

Tas darbojas ar divām kāršu kaudzītēm. Viena no tām saucas A, otra - B. Ir trešā kaudzīte, kas sākumā ir tukša un ko sauc par C. Beigās tajā būs rezultāts.

1. Ja A vai B kaudze ir tukša, visas tās kaudzes kārtis, kas nav tukšas, novietojiet uz C kaudzes; viss ir izdarīts, C kaudze ir apvienošanas rezultāts. (Piezīme: paņemiet visu kaudzīti un novietojiet to uz C kaudzītes; ja to darīsiet pa kartēm, mainīsies kārtība, un tas nedarbosies tā, kā vajadzētu.)
2. Aplūkojiet A un B kaudzes augšējās kārtis. Kārtiņu ar mazāku numuru novietojiet C kaudzes augšpusē. Ja C kaudzē nebija nevienas kārtis, tagad tajā būs viena kārts.
3. Ja A vai B kaudzītē ir palikušas kārtis, atgriezieties pie 1. soļa, lai tās sakārtotu.

Vēsture

Šo algoritmu 1945. gadā izstrādāja Džons fon Neimans. Viņš to nesauca par šķirošanu pēc skaitļiem, bet gan par Mergesort. Tas ir ļoti labs šķirošanas algoritms, salīdzinot ar citiem.

Trešais algoritms

Pirmā algoritma karšu šķirošana aizņem daudz vairāk laika nekā otrā, taču to var uzlabot (padarīt labāku). Aplūkojot burbuļveida šķirošanu, var pamanīt, ka kārtis ar lieliem skaitļiem no kaudzes augšas pārvietojas diezgan ātri, bet kartēm ar maziem skaitļiem kaudzes apakšā ir vajadzīgs ilgs laiks, lai paceltos (pārvietotos uz augšu). Lai uzlabotu pirmo algoritmu, ir šāda ideja:

Tā vietā, lai salīdzinātu divas blakus esošas kārtis, sākumā tiek izvēlēta "īpaša" karte. Pēc tam visas pārējās kartes tiek salīdzinātas ar šo karti.

1. Sākam ar kaudzi A. Vēl būs divas citas kaudzes B un C, kas tiks izveidotas vēlāk.
2. Ja kaudzē A nav karšu vai ir tikai viena karte, šķirošana ir pabeigta.
3. No A kaudzes tiek izvēlēta kārts, ja iespējams, pēc nejaušības principa. To sauc par šarnīru.
4. Visas atlikušās A kaudzes kārtis tiek salīdzinātas ar šo šarnīru. Kartes ar mazāku skaitu nonāk B kaudzītē, bet tās, kurām ir vienāds vai lielāks skaits, nonāk C kaudzītē.
5. Ja B vai C kaudzēs ir kādas kārtis, šīs kaudzes ir jāsašķiro ar to pašu algoritmu (Sākt no 1. pozīcijas šajā sarakstā gan B, gan C kaudzē pēc kārtas).)
6. Paveikts. Sakārtotajā kāršu kaudzē vispirms ir sakārtotā kaudze B, tad šarnīrs un tad sakārtotā kaudze C.

Vēsture

Šo algoritmu 1960. gadā izstrādāja K. A. R. Hūrs. Mūsdienās tas ir viens no visplašāk izmantotajiem šķirošanas algoritmiem. To sauc par Quicksort.

Animācija, kas parāda, kā darbojas burbuļu šķirošana


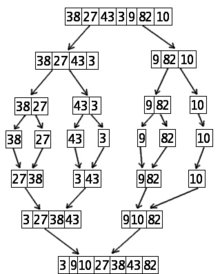
7 skaitļu šķirošana, izmantojot otro šķirošanas pēc skaitļiem algoritmu (Mergesort)


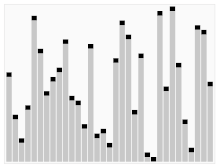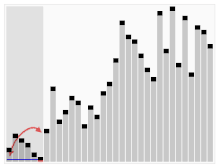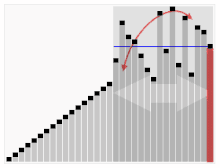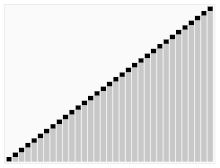
Trešais kāršu šķirošanas algoritms. Elements ar sarkano joslu tiek izvēlēts kā ass. Sākumā tas ir elements, kas atrodas pa labi. Šo algoritmu sauc par Quicksort.

Algoritmu salikšana kopā

Ja spēlētājiem ir kārtis ar krāsām un cipariem, viņi var tās sašķirot pēc krāsas un skaitļa, ja veic "šķirošanas pēc krāsām" algoritmu, tad veic "šķirošanas pēc cipariem" algoritmu katrai krāsainai kaudzītei un tad saliek kaudzītes kopā.

Šķirošanas pēc skaitļiem algoritmus ir grūtāk veikt nekā šķirošanas pēc krāsām algoritmus, jo var nākties atkārtot darbības vairākas reizes. Varētu teikt, ka šķirošana pēc skaitļiem ir sarežģītāka.

Saistītās lapas

• Eiklīda algoritms tika atrasts pirms vairāk nekā 2000 gadiem. Ar to var atrast divu skaitļu lielāko kopīgo dalītāju.