Algebra

Vēsture

Agrīnās algebras formas izstrādāja babilonieši un grieķu ģeometri, piemēram, Aleksandrijas Hēro. Tomēr vārds "algebra" ir arābu vārda Al-Jabr ("liešana") latīņu valodas forma, un tas cēlies no matemātikas grāmatas Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Esejā par liešanas un vienādojuma aprēķināšanu"), ko 9. gadsimtā sarakstīja persiešu matemātiķis Muhameds ibn Mūsā al-Khwārizmī, kurš bija musulmanis, dzimis Hvarizmā, Uzbekistānā. Viņš uzplauka Al-Ma'mūna laikā Bagdādē, Irākā, 813.-833. gadā un nomira ap 840. gadu. Šī grāmata 12. gadsimtā tika atvesta uz Eiropu un pārtulkota latīņu valodā. Pēc tam grāmata ieguva nosaukumu "Algebra". (Matemātiķa vārda galotne al-Khwarizmi tika pārveidota par vārdu, ko latīņu valodā bija vieglāk izrunāt, un tā kļuva par angļu valodas vārdu algorithm).

Piemēri

Šeit ir vienkāršs algebras problēmas piemērs:

Sue ir 12 konfektes, bet Ann ir 24 konfektes. Viņas nolemj dalīties, lai viņām būtu vienāds konfekšu skaits. Cik daudz konfekšu būs katrai?

Šie ir soļi, ko varat izmantot, lai atrisinātu problēmu:

1. Lai Annai būtu vienāds konfekšu skaits, viņai dažas ir jāatdod Sue. Lai x ir konfekšu skaits, ko Ann dod Sue.
2. Sjū konfektēm plus x ir jābūt vienādām ar Annas konfektēm mīnus x. Tas ir rakstāms šādi: 12 + x = 24 - x
3. No abām vienādojuma pusēm atņemiet 12. Tādējādi iegūstam: x = 12 - x. (Lai vienādojums joprojām būtu patiess, tam, kas notiek vienā vienādojuma pusē, jānotiek arī otrā pusē. Tātad šajā gadījumā, kad no abām malām atņēma 12, radās vidējais solis 12 + x - 12 = 24 - x - 12. (2 ) Tātad, kad no abām malām atņēma 12, radās vidējais solis 12 + x - 12 = 24 - x - 12. Pēc tam, kad cilvēks ar to ir apmierināts, vidējais solis netiek pierakstīts.)
4. Pievienojiet x abām vienādojuma pusēm. Tādējādi iegūstam: 2x = 12
5. Abas vienādojuma puses daliet ar 2. Tādējādi iegūstiet x = 6. Atbilde ir seši. Ja Anna iedos Sjū 6 konfektes, viņām būs vienāds konfekšu skaits.
6. Lai to pārbaudītu, ielieciet 6 atpakaļ sākotnējā vienādojumā, kur bija x: 12 + 6 = 24 - 6.
7. Tādējādi iegūstam 18=18, kas ir taisnība. Katram no viņiem tagad ir 18 konfektes.

Praksē algebru var izmantot, kad jāsaskaras ar problēmu, kuru ir pārāk grūti atrisināt citādā veidā. Lai atrisinātu tādas problēmas kā automaģistrāles būvniecība, mobilā tālruņa projektēšana vai kādas slimības ārstēšanas līdzekļa atrašana, ir nepieciešama algebra.

Algebras rakstīšana

Tāpat kā lielākajā daļā matemātikas daļu, pievienojot z y (vai y plus z), to raksta kā y + z. Atņemot z no y (vai y mīnus z), to raksta kā y - z. Dalot y ar z (vai y virs z: y z {\displaystyle y \pār z} ), to raksta kā y ÷ z vai y/z. Biežāk lieto y/z.

Algebrā y reizināšanu ar z (vai y reiz z) var pierakstīt 4 veidos: y × z, y * z, y-z vai vienkārši yz. Parasti reizināšanas simbols "×" netiek lietots, jo tas pārāk atgādina burtu x, kas bieži tiek lietots kā mainīgais. Arī reizinot lielāku izteiksmi, var izmantot iekavās: y (z+1).

Kad algebrā reizinām skaitli un burtu, burta priekšā rakstām skaitli: 5 × y = 5y. Ja skaitlis ir 1, tad 1 nav rakstāms, jo 1 reiz jebkurš skaitlis ir šis skaitlis (1 × y = y), tāpēc tas nav vajadzīgs.

Papildus jāpiebilst, ka algebrā nav jālieto burti x vai y. Mainīgie ir tikai simboli, kas apzīmē kādu nezināmu skaitli vai vērtību, tāpēc var izmantot jebkuru mainīgo. x un y ir visizplatītākie.

Funkcijas un grafiki

Svarīga algebras daļa ir funkciju izpēte, jo funkcijas bieži parādās vienādojumos, kurus mēs mēģinām atrisināt. Funkcija ir kā mašīna, kurā var ievietot skaitli (vai skaitļus) un iegūt noteiktu skaitli (vai skaitļus). Izmantojot funkcijas, grafiki var būt spēcīgs instruments, kas palīdz mums pētīt vienādojumu risinājumus.

Grafiks ir attēls, kurā parādītas visas mainīgo vērtības, kas padara vienādojumu vai nevienādību patiesu. Parasti to ir viegli izveidot, ja ir tikai viens vai divi mainīgie. Grafiks bieži vien ir līnija, un, ja līnija nav līkne vai neiet taisni uz augšu un uz leju, to var aprakstīt ar pamatformulu y = mx + b. Mainīgais b ir grafika y-intercepts (vieta, kur līnija šķērso vertikālo asi), bet m ir līnijas slīpums jeb stāvums. Šī formula attiecas uz grafika koordinātēm, kur katrs līnijas punkts ir rakstīts (x, y).

Dažos matemātikas uzdevumos, piemēram, taisnes vienādojumā, var būt vairāk nekā viens mainīgais (šajā gadījumā x un y). Lai atrastu punktus uz taisnes, tiek mainīts viens mainīgais. Mainīgo, kas tiek mainīts, sauc par "neatkarīgo" mainīgo. Tad tiek veikti matemātiskie aprēķini, lai iegūtu skaitli. Iegūto skaitli sauc par "atkarīgo" mainīgo. Lielākoties neatkarīgais mainīgais lielums tiek rakstīts kā x, bet atkarīgais mainīgais lielums - kā y, piemēram, y = 3x + 1. To bieži attēlo grafikā, izmantojot x asi (pa kreiso un labo pusi) un y asi (pa augšu un leju). To var rakstīt arī funkcijas formā: f(x) = 3x + 1. Tātad šajā piemērā x vietā var ierakstīt 5 un iegūt y = 16. Ievietojot 2 kā x, iegūtu y = 7. Ja x ierakstītu 0, iegūtu y=1. Tātad caur punktiem (5,16), (2,7) un (0,1) būtu līnija, kā redzams grafikā pa labi.

Ja x ir 1, tad tā ir taisne. Ja tā ir kvadrāts vai kāda cita lielība, tā būs izliekuma līkne. Ja tā izmanto nevienādību (< vai > ), tad parasti daļa grafika ir ēnota - vai nu virs, vai zem līnijas.

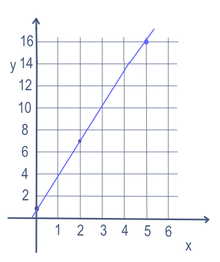
Lineārais vienādojums y=3x+1

Algebras noteikumi

Algebrā ir daži noteikumi, kurus var izmantot, lai labāk izprastu vienādojumus. Tos sauc par algebras noteikumiem. Lai gan šie noteikumi var šķist bezjēdzīgi vai acīmredzami, ir prātīgi saprast, ka šīs īpašības nav spēkā visās matemātikas nozarēs. Tāpēc būs noderīgi uzzināt, kā šie aksiomātiskie noteikumi ir deklarēti, pirms pieņemt tos par pašsaprotamiem. Pirms pāriet pie noteikumiem, pārdomājiet divas definīcijas, kas tiks dotas.

1. Pretstats - {\displaystyle a} pretstats ir - a {\displaystyle -a} .
2. Reciprocitāte - a {\displaystyle a} savstarpējais lielums ir 1 a {\displaystyle {\frac {1}{a}}}. .

Noteikumi

Saskaitīšanas komutatīvā īpašība

"Komutatīvais" nozīmē, ka funkcijai ir tāds pats rezultāts, ja skaitļi tiek apmainīti. Citiem vārdiem sakot, vienādojuma locekļu secībai nav nozīmes. Ja divu locekļu operators ir saskaitīšana, tad ir piemērojama "komutatīvā saskaitīšanas īpašība". Algebriskā izteiksmē tas dod a + b = b + a {\displaystyle a+b=b+a} .

Ņemiet vērā, ka tas neattiecas uz atņemšanu! (t.i., a - b ≠ b - a {\displaystyle a-b\neq b-a} ).

Komutatīvā īpašība reizināšanai

Ja divu locekļu operators ir reizinājums, tad ir piemērojama "komutatīvā reizināšanas īpašība". Algebriskā izteiksmē tas dod a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} .

Ņemiet vērā, ka tas neattiecas uz dalīšanu! (t.i. a b ≠ b a {\displaystyle {\frac {a}{b}}}neq {\frac {b}{a}}}}}. ja a ≠ b {\displaystyle a\neq b} ).

Pievienotības asociatīvā īpašība

"Asociatīvais" attiecas uz skaitļu grupēšanu. Saskaitīšanas asociatīvā īpašība nozīmē, ka, saskaitot trīs vai vairāk locekļus, nav svarīgi, kā šie locekļi ir sagrupēti. Algebriski tas dod a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Ievērojiet, ka tas neattiecas uz atņemšanu, piemēram, 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} (skat. sadalījuma īpašību).

Asociatīvā reizināšanas īpašība

No reizināšanas asociatīvās īpašības izriet, ka, reizinot trīs vai vairāk locekļus, nav svarīgi, kā šie locekļi ir sagrupēti. Algebriski tas dod a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} . Ievērojiet, ka tas neattiecas uz dalīšanu, piemēram, 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} .

Sadalījuma īpašība

Sadalījuma īpašība nosaka, ka skaitļa reizinājumu ar citu locekli var sadalīt. Piemēram: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} . (Nejauciet to ar asociatīvajām īpašībām! Piemēram, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .)

Aditīvās identitātes īpašība

"Identitāte" ir skaitļa īpašība, ka tas ir vienāds pats ar sevi. Citiem vārdiem sakot, eksistē divu skaitļu operācija, lai tā būtu vienāda ar summas mainīgo. Aditīvās identitātes īpašība nosaka, ka jebkura skaitļa un 0 summa ir šis skaitlis: a + 0 = a {\displaystyle a+0=a} . Tas attiecas arī uz atņemšanu: a - 0 = a {\displaystyle a-0=a} .

Multiplikatīvās identitātes īpašība

Multiplikatīvās identitātes īpašība nosaka, ka jebkura skaitļa un 1 reizinājums ir šis skaitlis: a ⋅ 1 = a {\displaystyle a\cdot 1=a} . Tas attiecas arī uz dalīšanu: a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Aditīvā apgrieztā īpašība

Aditīvā apgrieztā īpašība ir nedaudz līdzīga aditīvās identitātes īpašībai. Ja operācija ir skaitļa un tā pretī esošā skaitļa summa un tā ir vienāda ar 0, tad šī operācija ir derīga algebriska operācija. Algebriski tas nosaka: a - a = 0 {\displaystyle a-a-a=0} . 1 aditīvais apgrieztais skaitlis ir (-1).

Multiplikatīvā apgrieztā īpašība

Multiplikatīvā apgrieztā īpašība nozīmē, ka tad, ja operācija ir skaitļa un tā apgrieztā reizinājums un tā ir vienāda ar 1, šī operācija ir derīga algebriska operācija. Algebriski tas nosaka: a a a = 1 {\displaystyle {\frac {a}{a}}=1} . 2 apgrieztā reizinātāja ir 1/2.

Uzlabotā algebra

Papildus "elementārajai algebrai" jeb pamata algebrai koledžās un universitātēs tiek mācīti arī tādi sarežģīti algebras veidi kā abstraktā algebra, lineārā algebra un universālā algebra. Tas ietver arī to, kā izmantot matricu, lai atrisinātu daudzus lineāros vienādojumus vienlaicīgi. Abstraktā algebra ir mācība par lietām, kas atrodamas vienādojumos, sniedzoties tālāk par skaitļiem un pārejot uz abstraktākām lietām ar skaitļu grupām.

Daudzas matemātikas problēmas ir saistītas ar fiziku un inženierzinātnēm. Daudzās no šīm fizikas problēmām laiks ir mainīgais lielums. Laikam izmanto burtu t. Algebras pamatideju izmantošana var palīdzēt samazināt matemātisko problēmu līdz tās vienkāršākajai formai, tādējādi atvieglojot sarežģītu problēmu risināšanu. Enerģija ir e, spēks ir f, masa ir m, paātrinājums ir a, un gaismas ātrums dažkārt ir c. To izmanto dažos slavenos vienādojumos, piemēram, f = ma un e = mc^2 (lai gan, lai izveidotu pēdējo vienādojumu, bija vajadzīga sarežģītāka matemātika, kas pārsniedz algebru).

Saistītās lapas

• Matemātikas tematu saraksts
• Darbību secība
• Parabola
• Datoralgebras sistēma