Reizināšana matemātikā — definīcija, īpašības un piemēri

Uzzini reizināšanas definīciju, īpašības un saprotamus piemērus — no pamatiem līdz sarežģītākiem gadījumiem, ar praktiskām paskaidrojošām ilustrācijām skolēniem un skolotājiem.

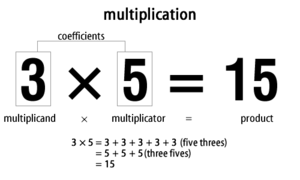
Reizināšana (dažreiz saukta arī par daudzināšanu) ir pamatdarbība ar skaitļiem — aritmētiska operācija, ar kuru iegūst divu skaitļu reizinājumu. Vienkāršākais izpratnes līmenis ir atkārtota saskaitīšana — piemēram, 3 × 5 nozīmē pievienot trīs piecas reizes (3 + 3 + 3 + 3 + 3 = 15). Tomēr reizināšana ir daudz plašāka: tas attiecas uz dabiskajiem skaitļiem, reālajiem skaitļiem, racionālajiem skaitļiem un kompleksajiem skaitļiem, kā arī to interpretācijas ģeometrijā, skaitļu teorijā un citur.

Pamatformulas un rakstība

Parasti reizinājumu pieraksta kā a × b = c vai a·b = c, dažkārt izmanto arī vienkāršāku pierakstu bez zīmes, piemēram, ab. Abos reizināmie (a un b) tiek saukti par reizinātājiem, un rezultātu sauc par reizinājumu (produkts). Piemērs: 3 × 5 = 15 — var izlasīt kā „trīs reiz pieci ir piecpadsmit”.

Interpretācijas

• Atkārtota saskaitīšana: dabiskajiem skaitļiem a × b nozīmē summu, kurā a tiek pieskaitīts b reizes (vai otrādi).
• Platuma interpretācija: izmantojot reālos skaitļus, reizināšana var dot taisnstūra laukumu: ja viena mala ir a un otra b, tad laukums = a × b.
• Mērogošana: reizināšana mēro vērtību; piemēram, reizinot vektoru vai skaitli ar skalāra faktoru, tiek mainīts tā garums vai mērogs.
• Kardinālie lielumi: definīcija kā atkārtota saskaitīšana ļauj interpretēt kardinālo skaitļu reizināšanu (skaitu produktu).

Pamatīpašības

• Kommulatīvums: a × b = b × a. Tas ir spēkā parasti visiem dabiskajiem, reālajiem un kompleksajiem skaitļiem.
• Asociatīvums: (a × b) × c = a × (b × c). Tas ļauj viegli reizināt vairākus skaitļus kopā bez pārkārtošanas.
• Distributivitāte pār saskaitīšanu: a × (b + c) = a × b + a × c. Šī īpašība ir īpaši svarīga algebraiskos aprēķinos.
• Neitrālais elements: 1 ir reizināšanas identitāte: a × 1 = a.
• Nulles īpašība: a × 0 = 0 — jebkurš skaitlis, reizināts ar nulli, dod nulli.

Signu likumi un piemēri

• + × + = + (piemērs: 2 × 3 = 6)
• + × − = − (piemērs: 2 × −3 = −6)
• − × + = − (piemērs: −2 × 3 = −6)
• − × − = + (piemērs: −2 × −3 = 6)
• Daži piemēri: 3 × 5 = 15; (1/2) × (3/4) = 3/8; 2.5 × 4 = 10; (−3) × 0 = 0.

Reizināšana dažādās skaitļu sistēmās un struktūrās

Reizināšana tiek definēta un uzvedas atšķirīgi atkarībā no objekta:

• Veseli skaitļi, racionālie, reālie, kompleksi: reizināšana ir komutatīva, asociatīva un distributīva.
• Frakcijas un decimālskaitļi: reizināšanas princips saglabājas — reizinām pa daļām vai decimāldaļām. Frakciju reizināšana: (a/b) × (c/d) = (a×c)/(b×d).
• Matricas, vektori un kvaternioni: šajos gadījumos daudzām reizināšanas definīcijām nav komutatīvuma. Piemēram, matricu reizināšana parasti nav komutatīva; kvaternioni arī nav komutatīvi.
• Skalāri un vektori: skalārais reizinājums (dot product) atšķiras no skaldījuma ar vektora reizināšanu (cross product) un citām operācijām.

Kā reizināšana tiek izmantota praksē

• Ģeometrijā: laukumu, tilpumu, mērogu aprēķināšana.
• Fizikā: spēks × attālums = darbs; ātrums × laiks = ceļš.
• Finansēs: procentu aprēķini, izdevumu reizināšana.
• Datortehnikā un programmēšanā: efekti, transformācijas, matricas reizināšana attēlu apstrādē.

Skaitīšanas tabulas un algoritmi

Multiplikācijas tabula (reizināšanas tabula) no 1 līdz 10 vai 12 ir pamatprasmju apguvei. Rokraksta algoritmi ietver garo reizināšanu (long multiplication), kas ir noderīgs lielu veselību skaitļu reizināšanai, un daudzi īsie paņēmieni — piemēram, reizināšana ar 10, 100 (vienkārši pievienojot nulles) vai izmantojot sadalīšanu (kā 14 × 25 = 14 × (100/4) = 350).

Teorētiskā nozīme

Matemātikā reizināšanai ir centrāla loma daudzās struktūrās: ringos, laukos, algebrās. Tā ļauj veidot polinomus, faktorizēt skaitļus un pētīt īpašības, piemēram, lielāko kopīgo dalītāju un primfaktorizāciju.

Atkārtotā definīcija un mērogošana

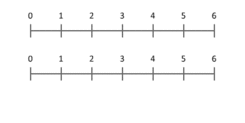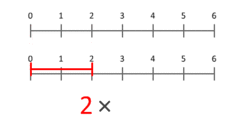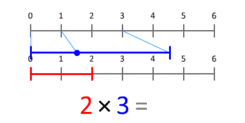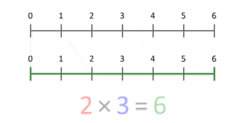
Kā minēts, reizināšana var tikt uztverta kā atkārtota saskaitīšana dabiskajos skaitļos, bet vispārīgāka un intuitīvā interpretācija ir mērogošana — viendabīgas objekta transformācijas, kas darbojas arī, ja reizināmais ir mazāks par 1 vai negatīvs. Tas palīdz saprast, kā 3 reizina ar 2 dod 6 arī geometriski vai kā skalāra reizināšana maina segmentu garumu.

Inverse operācija

Reizināšanas pretējs ir dalīšana: ja a × b = c un b ≠ 0, tad c ÷ b = a. Skaitlim a ir arī reizināšanas inversais elements 1/a (ja a ≠ 0), jo a × (1/a) = 1.

Kopsavilkums

• Reizināšana ir pamatdarbība, kuru var skatīt gan kā atkārtotu saskaitīšanu, gan kā mērogošanu.
• Tai piemīt būtiskas īpašības — komutatīvums (vairumā gadījumu), asociatīvums un distributivitāte pār saskaitīšanu.
• Ir svarīgi atcerēties signu likumus, identitātes elementu (1) un nulles īpašību.
• Daudzās matemātiskās struktūrās reizināšana var uzvesties citādi (piem., matricu reizināšana nav komutatīva), tādēļ jāņem vērā definīcija konkrētajā kontekstā.

Dažos mācību materiālos reizināšana tiek saukta arī par daudzināšanu, un matemātiķi abus reizināmos dažkārt sauc par "koeficientiem" vai vienkārši par reizinātājiem. Daudzinātājs × reizinātājs = reizinājums.

Jautājumi un atbildes

Q: Kas ir reizināšana?

J: Kā sauc divus reizināmos skaitļus?

J: Vai reizināšana ir komutatīva?

J: Kā mēs varam interpretēt kardinālo skaitļu reizināšanu?

J: Kā var attēlot trīs, kas reizināts ar pieci?

J: Kas ir pretējs reizinājumam?

Meklēt pēc burta