Vektors — definīcija, lielums, virziens un piemēri matemātikā
Vektors — definīcija, lielums, virziens un piemēri matemātikā. Saprotami skaidrojumi, grafiskais attēlojums, formulas un prakstiski piemēri, lai apgūtu vektoru jēdzienu soli pa solim.
Vektors ir matemātisks objekts, kam ir lielums, ko sauc par lielumu, un virziens.
Piemēram, vektoru var izmantot, lai parādītu attālumu un virzienu, kurā kaut kas pārvietojies. Ja jūs jautājat norādes, un cilvēks saka: "Ejiet vienu kilometru uz ziemeļiem", tas ir vektors. Ja viņš saka "Ejiet vienu kilometru", nenorādot virzienu, tas būtu skalārs.
Vektorus parasti zīmējam kā bultas. Bultas garums ir proporcionāls vektora lielumam. Virziens, kurā bultiņa rāda, ir vektora virziens.
Pamatjēdzieni
Apzīmējums: Vektoru parasti apzīmē ar burtu (piem., v) — dažreiz treknrakstā vai ar bultiņu virs burta. Lielums (magnitūda) bieži apzīmē ar |v| un tas ir skaitlis, kas rāda, cik garš vektors ir. Virziens norāda, kurā pusē vektors "rāda".
Nullvektors: Vektors ar lielumu nulle, kas nav vērsts neviena konkrētā virzienā. Parasti apzīmē kā 0.
Vienības vektors: Vektors ar lielumu 1. To izmanto, lai norādītu virzienu bez mēroga ietekmes. Ja v ir nenulles vektors, tā vienības vektors ir v/|v|.
Koordinātvektori un lieluma formula
Raugoties koordinātēs, vektoru var raksturot ar komponentēm. Piemēram:
- 2D vektors: v = (x, y)
- 3D vektors: v = (x, y, z)
Vektora lielumu aprēķina pēc Pitagora teoremas uz komponentēm: |v| = sqrt(x^2 + y^2) (2D), |v| = sqrt(x^2 + y^2 + z^2) (3D).
Piemērs: ja v = (3, 4), tad |v| = sqrt(3^2 + 4^2) = 5.
Vektoru operācijas
- Saskaitīšana (ģeometriski): paralelograma likums vai gala‑uz‑sākuma likums. Algebraiski: (x1, y1) + (x2, y2) = (x1+x2, y1+y2).
- Atņemšana: u − v = (u1 − v1, u2 − v2).
- Skalāra reizināšana: a·v = (a x, a y). Tas mērogo vektoru; ja a<0, virziens tiek apgriezts.
- Skalārais reizinājums (punktveida, dot product): u·v = u1v1 + u2v2 (+ u3v3 3D). Tas saista vektoru komponentes un dod skaitli. Geometriski u·v = |u||v|cos θ, kur θ ir leņķis starp vektoriem. Piemērs: (1,2)·(3,4) = 1·3 + 2·4 = 11.
- Krusta reizinājums (3D): u × v ir 3D vektors, kas ir perpendikulārs gan u, gan v; tā lielums |u×v| = |u||v| sin θ. Piemērs: (1,0,0) × (0,1,0) = (0,0,1).
Leņķis un projekcija
Leņķi starp vektoriem var atrast ar skalāro reizinājumu: cos θ = (u·v) / (|u||v|). Vektora projekcija uz w ir proj_w(u) = (u·w / |w|^2) w; tā rāda u komponenti virzienā w.
Īpašības
- Vektoru saskaitīšana ir komutatīva un asociatīva: u+v = v+u, (u+v)+w = u+(v+w).
- Distributivitāte: a(u+v) = au + av.
- Nullvektors un pretvektors: u + 0 = u; u + (−u) = 0.
Piemēri pielietojumos
- Fizika: ātrums, paātrinājums, spēks un impulss — visi ir vektori, jo tiem ir gan lielums, gan virziens.
- Ģeometrija un navigācija: pārvietošanās (deplasācija) no punkta A uz B tiek aprakstīta ar vektoru; piemēram, "2 km uz austrumiem un 1 km uz ziemeļiem" var attēlot kā vektoru kombināciju.
- Datorgrafika: virzieni, normāles, shēmas transformācijām un apgaismojuma aprēķiniem izmanto vektorus un to operācijas.
Kopsavilkums
Vektors ir fundamentāls rīks matemātikā un dabaszinātnēs: tas apvieno lielumu un virzienu, ļauj veikt ģeometriskas un algebraiskas manipulācijas (saskaitīt, reizināt ar skaitli, aprēķināt leņķi un projekcijas) un ir plaši pielietojams ikdienas un speciālajās situācijās.
Vektoru piemēri
Skalāru piemēri
- Attālums starp divām vietām ir 10 kilometri. Šis attālums nav vektors, jo tajā nav norādīts virziens.
- Augļu skaits kastē nav vektors.
- Persona, kas norāda, nav vektors, jo ir tikai virziens. Nav lieluma (piemēram, attālums no cilvēka pirksta līdz ēkai).
- Objekta garums.
- Automašīna brauc ar ātrumu 100 kilometri stundā. Tas neapraksta vektoru, jo ir tikai lielums, bet nav virziena.
Vairāk vektoru piemēru
- Pārvietojums ir vektors. Pārvietojums ir attālums, par kādu kaut kas pārvietojas noteiktā virzienā. Attāluma mērvienība ir skalārs.
- Spēks, kas ietver virzienu, ir vektors.
- Ātrums ir vektors, jo tas ir ātrums noteiktā virzienā.
- Paātrinājums ir ātruma izmaiņu ātrums. Objekts paātrinās, ja tas maina ātrumu vai virzienu.
Kā pievienot vektorus
Vektoru pievienošana uz papīra, izmantojot "no galvas uz asti" metodi
Vektoru saskaitīšanas metode "no galvas uz asti" ir noderīga, lai uz papīra novērtētu divu vektoru saskaitīšanas rezultātu. Lai to izdarītu:
- Katrs vektors ir uzzīmēts kā bulta ar garuma vienību aiz tās, kur katra garuma vienība uz papīra apzīmē noteiktu vektora lielumu.
- Uzzīmējiet nākamo vektoru tā, lai otrā vektora astes(gala) punkts būtu pirmā vektora galvas(priekšpuses) punktā.
- Atkārtojiet to visiem turpmākajiem vektoriem: Nākamā vektora asti uzzīmējiet pie iepriekšējā vektora galvas.
- Novelciet līniju no pirmā vektora astes līdz pēdējā vektora galvai - tā ir visu vektoru rezultante (summa).
To sauc par metodi "no galvas uz asti", jo katra iepriekšējā vektora galva ved uz nākamā vektora asti.
Komponentu formas izmantošana
[ir nepieciešams paskaidrot d]
Komponentu formas izmantošana divu vektoru saskaitīšanai burtiski nozīmē vektoru komponenšu saskaitīšanu, lai izveidotu jaunu vektoru. Piemēram, lai a un b ir divi divdimensiju vektori. Šos vektorus var pierakstīt kā to komponentes.
a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})} 
b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})} 
Pieņemsim, ka c ir šo divu vektoru summa, tātad c = a + b. Tas nozīmē, ka c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} 
.
Šeit ir divu vektoru saskaitīšanas piemērs, izmantojot to sastāvdaļu formas.
a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)} 
b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)} 
c = a + b {\displaystyle \mathbf {c} =\mathbf {a} +\mathbf {b} } 
= ( a x + b x , a y + b y ) {\displaystyle =(a_{x}+b_{x},a_{y}+b_{y})} 
= ( 3 + 2 , - 1 + 2 ) {\displaystyle =(3+2,-1+2)} 
= ( 5 , 1 ) {\displaystyle =(5,1)} 
Šī metode darbojas ar visiem vektoriem, ne tikai divdimensiju vektoriem.
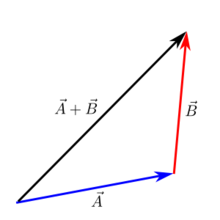
Papildinājums no galvas līdz astei
Kā reizināt vektorus
Punktu reizinājuma izmantošana
Dot reizinājums ir viena no vektoru reizināšanas metodēm. Tā rezultātā iegūst skalāru. Tā izmanto komponentu formu:
a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\displaystyle {\begin{aligned}\mathbf {a} =(2,3)\\\\mathbf {b} =(1,4)\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\=(2\cdot 1)+(3\cdot 4)\\=2+12=14\end{aligned}}}} 
Izmantojot krustenisko reizinājumu
Šķērsdarinājums ir vēl viena vektoru reizināšanas metode. Tā rezultātā iegūst citu vektoru. Izmantojot komponentu formu:
a × b = | a | | | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n} } 
Šeit | a | {\displaystyle |\mathbf {a} |} 
ir garums {\displaystyle \mathbf {a} } 
un n {\displaystyle \mathbf {n} } 
ir vienības vektors taisnā leņķī pret abiem a {\displaystyle \mathbf {a}. } un b {\displaystyle \mathbf {b} } 
.
reizināšana ar skalāru
Lai reizinātu vektoru ar skalāru (parastu skaitli), skaitli reizina ar katru vektora sastāvdaļu:
c x = ( c x 1 , c x 2 , . . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})} } 
Kā piemēru var minēt
c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\displaystyle {\begin{aligned}c=5\\\\mathbf {x} =(3,4)\\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\=(15,20)\end{aligned}}}} 
Saistītās lapas
- Vektorgrafika
- Vektoru lauks
Jautājumi un atbildes
J: Kas ir vektors?
A: Vektors ir matemātisks objekts, kam ir lielums, ko sauc par lielumu, un virziens. To bieži attēlo ar trekniem burtiem vai kā līnijas posmu no viena punkta uz otru.
J: Kā mēs parasti zīmējam vektorus?
A: Parasti vektorus zīmējam kā bultas. Bultas garums ir proporcionāls vektora lielumam, un virziens, uz kuru bulta norāda, ir vektora virziens.
J: Ko nozīmē, ja kāds jautā virzienu?
A: Ja kāds, prasot norādes, saka: "Ej vienu kilometru uz ziemeļiem", tas būtu vektors, bet, ja viņš saka: "Ej vienu kilometru", nenorādot virzienu, tas būtu skalārs.
J: Kādi ir daži piemēri, kā var izmantot vektorus?
A: Vektorus var izmantot, lai parādītu attālumu un virzienu, kurā kaut kas pārvietojies. Tos var arī izmantot, kad jājautā par virzienu vai jāorientējas apgabalā.
J: Kā vektorus attēlo matemātiski?
A: Vektorus bieži attēlo ar trekniem burtiem (piemēram, u, v, w) vai kā līnijas posmu no viena punkta uz otru (kā A→B).
J: Ko nozīmē, ja kaut ko sauc par skalāru?
A: Ja kaut ko sauc par skalāru, tas nozīmē, ka ar to nav saistīta virziena informācija, bet tikai skaitliskas vērtības, piemēram, attālums vai ātrums.
Meklēt