Dalīšana matemātikā — definīcija, simboli, kvocients un atlikums

Uzzini dalīšanu matemātikā: definīcija, simboli (÷, /, x/y), kvocienta aprēķins un atlikuma piemēri — skaidri paskaidrojumi un praktiski piemēri.

Autors: Leandro Alegsa

Matemātikā vārds "dalīšana" nozīmē darbību, kas ir pretēja reizināšanai. Daži dalīšanas simboli var būt slīpsvītra, līnija vai dalīšanas zīme ( ÷ {\displaystyle \div }{\displaystyle \div } ), piemēram:

6 / 3 {\displaystyle 6/3\,} vai{\displaystyle 6/3\,}6 3 {\displaystyle {\frac {6}{3}}} vai {\displaystyle {\frac {6}{3}}}6 ÷ 3. {\displaystyle 6\div 3.} {\displaystyle 6\div 3.}

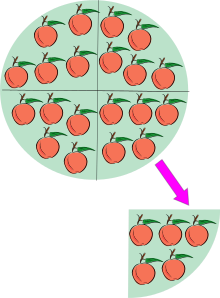
Katrs no šiem trim skaitļiem nozīmē "6 dalīts ar 3", un atbilde ir 2. Pirmais skaitlis ir dalāmais (dividenze) — šeit 6, bet otrais skaitlis ir dalītājs — šeit 3. Rezultāts (jeb atbilde) ir kvantients. Veseliem skaitļiem jebkuru atlikušo summu sauc par "atlikumu" (piemēram, 14/4 dod 3, bet atlikums ir 2, jo skaitlis 3+2⁄4, tas pats, kas 3+1⁄2 vai 3,5).

Skaitļi var būt ļoti lieli, piemēram, divi simti: 200/5 = 40 vai 7 miljardi: 7 000 000 000 000 / 1000 = 7 000 000 000 (ir 7 miljoni).

Kas ir dalīšana — īsi un saprotami

Dalīšana ir darbība, ar kuru mēs noskaidrojām, cik reizes viens skaitlis (dalītājs) iet citā skaitlī (dalāmais). Ja dalās precīzi bez atlikuma, sakām, ka dalāmais ir dalāms ar dalītāju vai ka dalīšana ir bezatliekuma (piem., 6 ÷ 3 = 2). Ja paliek atlikums, to pieraksta kā veselu daļu un atlikumu vai kā decimāldaļu (piem., 14 ÷ 4 = 3 ar atlikumu 2, tas pats kā 3,5).

Galvenie termini

  • Dalāmais (dividenze) — skaitlis, kuru dalām (piem., 6).
  • Dalītājs — skaitlis, ar kuru dalām (piem., 3).
  • Kvocients — dalīšanas rezultāts (piem., 2).
  • Atlikums — tas, kas paliek pāri, ja dalīšana neatdod precīzu veselu skaitli (piem., 14 ÷ 4 → atlikums 2).

Matemātiskā forma un teorēma

Euclida dalīšanas (Eiklīda dalīšanas) teikums: ja a un b ir veseli skaitļi un b ≠ 0, tad pastāv vienīgi tādi veseli skaitļi q (kvocients) un r (atlikums), ka

a = b · q + r, kur 0 ≤ r < |b|. Tas nozīmē, ka dalīšana ar veseliem skaitļiem dod unikālu kvocientu un atlikumu.

Dažādi dalīšanas veidi un pieraksti

  • Frakcijas: 6/3 vai {@literal \frac{6}{3}}.
  • Dalīšanas zīme: 6 ÷ 3.
  • Decimāldaļas: ja dalīšana nav bez atlikuma, bieži pieraksta rezultātu kā decimāldaļu (piem., 1 ÷ 4 = 0,25).
  • Reizināšanas pretējs: dalīšana ar b ir tas pats, kas reizināšana ar b apgriezto skaitli (reciprokā), t.i., a ÷ b = a × (1/b), ja b ≠ 0.

Svarīgas īpašības un piesardzība

  • Dalīšana nav komutatīva: a ÷ b nav tas pats kas b ÷ a.
  • Dalīšana nav asociatīva: (a ÷ b) ÷ c ≠ a ÷ (b ÷ c) kopumā.
  • Dalīšana ar nulli nav definēta: a ÷ 0 nav nozīmīgs darbības rezultāts matemātikā.
  • Ja atlikums ir 0, saka, ka dalāmais ir daļāms ar dalītāju (divisible).

Kā aprēķināt dalīšanu

Ir vairākas metodes: galda (galvu) aprēķins, īss dalīšanas veids, garais dalīšanas algoritms skolā, un modernās skaitļošanas metodes datoros. Garā dalīšana rāda pa posmiem, kā no kreisās uz labo iegūt kvocientu un atlikumu.

Piemēri

  • 6 ÷ 3 = 2 — precīza dalīšana, atlikums 0.
  • 14 ÷ 4 = 3 ar atlikumu 2, jo 14 = 4·3 + 2.
  • 1 ÷ 3 = 0,333... — dotais rezultāts ir atkārtojošs decimālskaitlis.
  • 200 ÷ 5 = 40 — piemērs ar lielākiem skaitļiem.
  • 7 miljardi: 7 000 000 000 000 ÷ 1000 = 7 000 000 000 (ir 7 miljoni) — rādījums, ka arī ar ļoti lieliem skaitļiem dalīšana darbojas tāpat.

Dalīšana programmēšanā un skaitļos

Programmēšanā parasti nodala veselu dalījumu (integer division) un realu skaitļu dalījumu: vesels dalījums 14 ÷ 4 bieži dod 3 (atlikums tiek ignorēts vai pieejams atsevišķi), bet reālais dalījums dod 3,5. Dažās valodās ir arī operācijas, kas atgriež atlikumu (modulo operācija).

Praktiskie padomi

  • Lai noteiktu, vai skaitlis ir daļāms ar 2, 5 vai 10, pietiek skatīties pēdējo ciparu; ar 3 vai 9 — summējot ciparus; ar 11 — izmantojot atbilstošu dalāmības testu.
  • Praksē izmanto dalīšanu, lai sadalītu resursus, aprēķinātu vidējos lielumus, konvertētu vienības, strādātu ar procentiem un daudzās citās ikdienas situācijās.

Dalīšana ir pamata aritmētiskā darbība, kas saprotama kā reizināšanas pretējā darbība, ar plašu pielietojumu gan teorētiskā matemātikā (piem., skaitļu teorijā), gan praktiskajās situācijās (finanses, inženierzinātnes, programmēšana u.c.).

Zoom

20 : 4 = 5 {\displaystyle 20:4=5} {\displaystyle 20:4=5}

Ar reizināšanu

Ja c reiz b ir vienāds ar a, rakstīts kā:

c × b = a {\displaystyle c\times b=a} {\displaystyle c\times b=a}

ja b nav nulle, tad a dalīts ar b ir vienāds ar c, un tas ir rakstīts šādi:

a b = c {\displaystyle {\frac {a}{b}}}=c} {\displaystyle {\frac {a}{b}}=c}

Piemēram,

6 3 = 2 {\displaystyle {\frac {6}{3}}=2} {\displaystyle {\frac {6}{3}}=2}

kopš

2 × 3 = 6 {\displaystyle 2\reiz 3=6}{\displaystyle 2\times 3=6} .

Iepriekšminētajā izteiksmē a sauc par dividendi, b - par dalītāju, bet c - par kvantientu.

Dalīšana ar nulli

x 0 = ? {\displaystyle {\frac {x}{0}}=? } {\displaystyle {\frac {x}{0}}=?}

...nav definēts.

Norāde

Dalīšanu visbiežāk attēlo, novietojot dividenžu virs dalītāja un starp tām novietojot horizontālu līniju, ko sauc arī par vinculum. Piemēram, a dalot ar b, raksta

a b . {\displaystyle {\frac {a}{b}}. } {\displaystyle {\frac {a}{b}}.}

To var skaļi nolasīt kā "a dalīts ar b" vai "a pār b". Dalījumu var izteikt vienā rindā, rakstot dividenzi, tad slīpsvītru, tad dalītāju, piemēram, šādi:

a / b . {\displaystyle a/b.\,} {\displaystyle a/b.\,}

Šis ir ierastais dalīšanas norādīšanas veids lielākajā daļā datorprogrammēšanas valodu, jo to var viegli ievadīt kā vienkāršu rakstzīmju secību.

Tipogrāfiskā variācija, kas ir pusceļā starp šīm divām formām, izmanto slīpsvītru, bet paaugstina dividenžu un pazemina dalītāju:

a⁄b .

Jebkuru no šīm formām var izmantot, lai attēlotu daļu. Daļa ir dalījuma izteiksme, kurā gan dividenze, gan dalītājs ir veseli skaitļi (lai gan parasti tos sauc par skaitītāju un saucēju). Daļa ir pieņemts skaitļu rakstīšanas veids. Ne vienmēr tiek sagaidīts, ka dalīšanas rezultāts tiek rakstīts ar decimāldaļām.

Mazāk izplatīts veids, kā parādīt dalījumu, ir izmantot obelus (vai dalījuma zīmi) šādā veidā:

a ÷ b . {\displaystyle a\div b. } {\displaystyle a\div b.}

Taču elementārajā aritmētikā šī forma tiek lietota diezgan bieži. Obelus tiek lietots arī kā vienīgais dalīšanas operācijas apzīmējums, piemēram, kā marķējums uz kalkulatora taustiņa.

Dažās citvalodīgās kultūrās "a dalīts ar b" tiek rakstīts a : b. Tomēr angļu valodā divkājis tiek lietots tikai, lai izteiktu saistīto attiecību jēdzienu (ar a : b kā "a ir ar b").

Saistītās lapas

Jautājumi un atbildes

J: Ko matemātikā nozīmē vārds "dalījums"?


A: Matemātikā dalīšana ir darbība, kas ir pretēja reizināšanai.

J: Kādi ir dalīšanas simboli?


A: Dalīšanas simboli ir slīpsvītra ( / ) un dalījuma līnija.

J: Kas ir dividenze dalīšanas uzdevumā?


A: Pirmais skaitlis dalīšanas uzdevumā tiek saukts par dividendi.

J: Kas ir dalītājs dalīšanas uzdevumā?


O: Otro skaitli dalīšanas uzdevumā sauc par dalītāju.

J: Kā sauc dalīšanas uzdevuma rezultātu?


A: Dalīšanas uzdevuma rezultātu sauc par kvantientu, bet jebkuru atlikušo veselu skaitli sauc par "atlikumu".

J: Vai dalot var izmantot lielus skaitļus?


A: Jā, dalot var izmantot ļoti lielus skaitļus, piemēram, divi simti vai septiņi miljardi.


Meklēt
AlegsaOnline.com - 2020 / 2025 - License CC3