Elementārā algebra — pamati, definīcija un piemēri skolēniem
Elementārā algebra — skaidri pamati, definīcijas un praktiski piemēri skolēniem. Saprotami skaidrojumi par mainīgajiem, vienādojumiem un risināšanu.
Elementārā algebra ir visvienkāršākā algebras pamatforma, ko parasti māca skolēniem. Tā parasti nāk pēc aritmētikas un ir daļa no plašākas matemātikas apguves. Ja aritmētikā darbina tikai konkrētus skaitļus un operatorus (+, −, ×, ÷), tad algebrā parādās mainīgie (piemēram, a, x, y), kas apzīmē nezināmus vai mainīgus skaitļus. Tas padara algebraisku pieeju noderīgu daudzos praktiskos uzdevumos.
Kāpēc algebra ir svarīga
- Tā ļauj risināt problēmas par "nezināmiem" skaitļiem un iepazīstina ar vienādojumiem un to risināšanas metodēm. Piemēram, atrisinot vienādojumu x, kur 3 x + 1 = 10 {\displaystyle 3x+1=10}
, mēs noskaidrojam, kāds skaitlis padara izteiksmi patiesu.
- Algebra ļauj vispārināt aritmētikas noteikumus. Ja, piemēram, redzam, ka 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}.
, tad var pierādīt, ka šāds princips darbojas vispārināti: a + b = b + a {\displaystyle a+b=b+a}
— tas palīdz attīstīt spēju domāt abstrakti.
- Algebra palīdz modelēt attiecības starp lielumiem — to sauc arī par funkcijām vai cēloņsakarībām. Piemēram, ja tiek pārdotas x biļetes, peļņa var būt izteikta kā 3 x - 10 {\displaystyle 3x-10}
dolāru — tas ļauj paredzēt rezultātu, mainot x.
Galvenie jēdzieni elementārajā algebrā
- Mainīgais (variabla) — simbols, kas apzīmē nezināmu vai mainīgu vērtību (piem., x, y).
- Konstante — skaitlis, kas nemainās (piem., 1, 3, 10).
- Izteiksme — kombinācija no skaitļiem, mainīgajiem un operatoriem, piemēram, 3x + 1.
- Koeficients — skaitlis, kas reizināts ar mainīgo (piem., skaitlis 3 izteiksmē 3x).
- Vienādojums — izteiksme, kurā divas formulas savieno ar vienādības zīmi (=), piemēram, 3x + 1 = 10. Mērķis bieži ir atrast x vērtību, kas apmierina vienādojumu.
- Nevienādība — izteiksme ar salīdzinājumu (<, >, ≤, ≥), kur meklējam mainīgo vērtības, kas apmierina nosacījumu.
- Funkcija — noteikums, kas katrai ievades vērtībai piešķir vienu izvadi; to bieži pieraksta kā f(x).
Vienkārši piemēri un soļi vienādojumu risināšanā
Risināšanas pamatprincipi: vienādojumā var veikt tās pašas darbības abās pusēs (pievienot, atņemt, reizināt, dalīt), lai nošķirtu mainīgo.
Piemērs 1 — lineārs vienādojums:
- Dots: 3x + 1 = 10 (3 x + 1 = 10 {\displaystyle 3x+1=10}
).
- Noņemam 1 no abām pusēm: 3x = 9.
- Dalām ar 3: x = 3.
- Pārbaudām: 3·3 + 1 = 10 — patiesi.
Piemērs 2 — vienkārša funkcija un interpretācija:
- Ja peļņa P ir P(x) = 3x − 10 (3 x - 10 {\displaystyle 3x-10}
), tad, ja pārdod 10 biļetes, peļņa būs P(10) = 3·10 − 10 = 20 dolāru.
Padomi skolēniem, kā efektīvi apgūt elementāro algebru
- Regulāri risini uzdevumus — algebra ir prasme, kas uzlabojas ar praksi.
- Sāc ar konkrētiem skaitļiem — pārbaudi izteiksmes, aizvietojot mainīgo ar skaitļiem, lai saprastu struktūru.
- Mācies soli pa solim — pieraksti visas darbības un pārliecinies, ka tās ir veiktas abās vienādojuma pusēs.
- Izmanto attēlus un grafikus — daudzas funkcijas ir vieglāk saprotamas, ja tās uzzīmē grafiski.
- Skaties kā piemēru modeļus — saprotot vienu parauguzdevumu, mēģini pielietot metodi līdzīgiem uzdevumiem.
- Ja nepieciešams, lūdz padomu no skolotāja vai izmanto resursus tiešsaistē un mācību grāmatās.
Elementāro algebru bieži izmanto arī citos mācību priekšmetos — piemēram, zinātnē, uzņēmējdarbībā un būvniecībā —, jo tā sniedz rīkus problēmu modelēšanai un risināšanai. Abstrakto algebru, kas ir daudz sarežģītāks temats, parasti māca vēlāk koledžā.
Vienkāršas algebras problēmas
Ja vienādojumam ir tikai viens nezināms skaitlis, to dažkārt ir viegli atrisināt. Nezināmo skaitli sauc par "x":
2 x + 4 = 12. {\displaystyle 2x+4=12.\,}
Lai atrisinātu vienkāršu vienādojumu ar vienu nezināmo, saskaitiet, atņemiet, reiziniet vai daliet abas vienādojuma puses ar vienu un to pašu skaitli, lai nezināmo summu x novietotu vienā vienādojuma pusē. Kad x atrodas vienā pusē, ar aritmētisko aprēķinu nosakiet summu, kas atrodas vienādojuma otrā pusē. Piemēram, atņemot 4 no abām iepriekš minētā vienādojuma pusēm:
2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4-4=12-4\,}
saņemšana:
2 x = 8 {\displaystyle 2x=8\,}
Abas malas dalot ar 2:
2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}},}
saņemšana:
x = 4. {\displaystyle x=4.\,}
Tas var palīdzēt domāt par šo vienādojumu kā par sniega pīli vai līdzsvaru, ko jūs darāt vienā pusē, jums ir jādara arī otrā pusē, un jūsu galvenais mērķis ir iegūt x pats par sevi.
Definīcijas
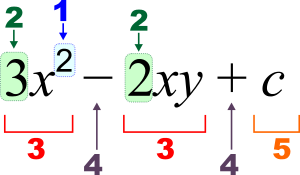
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c}
1 : eksponents (lielums), 2 : koeficients, 3 : loceklis, 4 : operators, 5 : konstante, x , y {\displaystyle x,y} : 
Jautājumi un atbildes
J: Kas ir elementārā algebra?
A: Elementārā algebra ir visvienkāršākā algebras forma, ko māca skolēniem. Tā parasti seko aritmētikai, un tajā izmanto mainīgos (piemēram, a, x, y), lai vienādojumos apzīmētu skaitļus.
J: Kādi ir daži elementārās algebras lietojumi?
A: Elementāro algebru var izmantot, lai risinātu nezināmu skaitļu uzdevumus, vispārinātu aritmētikas noteikumus, izprastu un veidotu funkcionālās sakarības, un to bieži izmanto daudzos citos mācību priekšmetos, piemēram, zinātnē, uzņēmējdarbībā un būvniecībā.
J: Kā elementārā algebra palīdz cilvēkiem saprast abstraktas idejas?
A: Elementārā algebra palīdz cilvēkiem apgūt vispārīgas idejas no daudziem piemēriem, pierādot, ka a+b=b+a visiem a un b. Tas ļauj labāk izprast abstraktus jēdzienus.
J: Vai abstraktā algebra ir sarežģītāka par elementāro algebru?
A: Jā, abstrakto algebru parasti māca vēlāk koledžā, un tā ir daudz sarežģītāka nekā elementārā algebra.
J: Kāda veida vienādojumus izmanto elementārajā algebrā?
A: Elementārā algebra ietver vienādojumus ar mainīgajiem (piemēram, a, x, y), kas apzīmē skaitļus, kā arī tādus operatorus kā +,- , × un ÷ .
3x+1=10 {\displaystyle 3x+1=10}
J: Kā elementārās algebras izpratne var palīdzēt citos mācību priekšmetos?
A: Elementārās algebras izpratne var palīdzēt citos mācību priekšmetos, piemēram, zinātnē, uzņēmējdarbībā vai būvniecībā, jo tā ļauj risināt nezināmu skaitļu problēmas un veidot funkcionālas sakarības starp dažādiem mainīgajiem.
Meklēt




