Nevienādība matemātikā — definīcija, simboli un piemēri
Nevienādība matemātikā: definīcija, simboli (<, >, ≤, ≥) un skaidri piemēri soli pa solim — saprotami skaidrojumi skolēniem un studentiem.
Nevienlīdzība ir tad, ja viens objekts ir:
- mazāks par otru ( a < b {\displaystyle \ a<b} nozīmē,
ka a ir mazāks par b).
- lielāks par otru ( a > b {\displaystyle \ a>b} nozīmē,
ka a ir lielāks par b).
- nav mazāks par otru ( a ≥ b {\displaystyle a\geq b}
nozīmē, ka a nav mazāks par b, t. i., tas ir vai nu lielāks, vai vienāds ar b).
- nav lielāks par otru ( a ≤ b {\displaystyle a\leq b}
nozīmē, ka a nav lielāks par b — tas ir, a ir mazāks vai vienāds ar b).
Dažkārt nevienlīdzību lieto, lai nosauktu apgalvojumu, ka viena izteiksme ir mazāka, lielāka, nav mazāka vai nav lielāka par otru.
Ko nozīmē stingrā un nestingrā nevienādība
Stingrās nevienādības apzīmē ar < un > (piem., a < b nozīmē, ka a ir stingri mazāks par b — tie nekad nav vienādi). Nestingrās (vai iekļaujošās) nevienādības apzīmē ar ≤ un ≥ (piem., a ≤ b nozīmē, ka a var būt mazāks vai vienāds ar b).
Galvenie noteikumi un likumi
- Pievienojot vai atņemot vienādu skaitli no abām pusēm, nevienādība saglabājas. Piem., ja a < b, tad a + c < b + c.
- Reizināšana vai dalīšana ar pozitīvu skaitli saglabā nevienādību: ja a < b un k > 0, tad ka < kb.
- Reizināšana vai dalīšana ar negatīvu skaitli apgriež nevienādību: ja a < b un k < 0, tad ka > kb (jāapgriež < vai > zīme).
- Transitivitāte: ja a < b un b < c, tad a < c.
Kā risina vienkāršas lineāras nevienādošanas
Risināšanas princips ir līdzīgs vienādojumu risināšanai — mērķis ir vienādojumā izolēt mainīgo, taču jāievēro nevienādību noteikumi (īpaši par zīmes apgriešanu, reizinot vai dalot ar negatīvu).
Piemērs 1: 2x + 3 < 7
- Atņem 3 no abām pusēm: 2x < 4
- Dalot ar 2 (pozitīvs): x < 2
- Risinājums intervālā: x ∈ (-∞, 2)
Piemērs 2 (reizināšana ar negatīvu): -2x > 6
- Dalot ar -2 (negatīvs), jāapgriež zīme: x < -3
Grafiska attēlošana uz skaitļu ass
Risinājumus parasti attēlo uz skaitļu ass ar:
- Atvērtu aplīti (vai bultu) — ja nevienādība ir stingra (< vai >).
- Aizvērtu punktu — ja nevienādība ir iekļaujoša (≤ vai ≥).
- Bultas, ja risinājums iet uz bezgalību (piem., x > 2 attēlo open circle pie 2 un bultu pa labi).
Intervālu pieraksts
Risinājumu kopas parasti izsaka ar intervālu pierakstu:
- x < 2 atbilst (-∞, 2)
- x ≤ 5 atbilst (-∞, 5]
- a ≤ x < b atbilst [a, b)
Sistēmas ar vairākām nevienādībām
Ja ir vairākas nevienādības vienā sistēmā, risinājums ir to risinājumu krustpunkts (kopiena). Piemēram, sistēma
1 < x ≤ 4
dotu risinājumu (1, 4].
Piemēri ikdienā
- Budžets: "Izdevumi nedrīkst pārsniegt 500 €" — ja x ir izdevumu summa, tad x ≤ 500.
- Auguma prasība: "Augstums jābūt vismaz 150 cm" — ja h ir augums, tad h ≥ 150.
Biežāk pieļautās kļūdas
- Aizmirst apgriezt nevienādības zīmi, dalot vai reizinot ar negatīvu skaitli.
- Neuzmanība, pārnesot locekļus no vienas puses uz otru (jāpārvērš pareizi ar pretējām darbībām).
Nevienādības ir fundamentāls rīks matemātikā, fizikā, ekonomikā un ikdienas situāciju modelēšanā — tās ļauj ierobežot, salīdzināt un definēt pieļaujamus vērtību diapazonus. Ja nepieciešams, varu pievienot vairāk praktisku uzdevumu ar risinājumiem vai grafiskiem piemēriem.
Darbs ar nevienādībām
Nevienlīdzība matemātikā ir tad, kad divi risinājumi vai atbildes tiek salīdzinātas ar lielāku par vai mazāku par. Tas ir tad, ja divi vai vēl daudzi risinājumi, kas tiek salīdzināti, nav vienādi lieli. Nevienādību atrisināt nozīmē atrast tās atrisinājumus. Ja mainīgajam aizstāj skaitli ar skaitli un apgalvojums ir patiess, tad tas ir atrisinājums. Ja mainīgajam tiek aizvietots skaitlis un apgalvojums nav patiess, tad šis skaitlis nav apgalvojuma atrisinājums.
Nevienlīdzība ir risinājuma atrašana dotajam mainīgajam. Tā ir kopas relatīvās kārtības atrašana. Nevienādībai ir daudzi risinājumi, bet ir jāatrod īstie risinājumi. Nevienādība ir reālo skaitļu atrisinājums. Nevienādības pareizi ir jālasa no kreisās puses uz labo, tāpat kā citus vienādojumus, bet vienīgā atšķirība ir tā, ka tiem ir atšķirīgi noteikumi katram vienādojumam.
Piemēram, x+4>12, kur x ir reāls skaitlis. Vispirms cilvēkam jāatrod x un jāzina, vai tas ir atrisinājums. Atbilde būs x>8, un tas ir patiess apgalvojums. Šis izteikums ir par x atrašanās vietu reālo skaitļu kopā. Skaitļu līnija ir viens no veidiem, kā parādīt atrašanās vietu attiecībā pret visiem pārējiem reālajiem skaitļiem (sk. 1. attēlu Nevienādība).
.jpg)
Nevienlīdzība 1 Šis ir vienādojuma x+4>12 risinājums.
Dažāda veida nevienādības
Ir pieci dažādi nevienlīdzības veidi:
- Pirmais no tiem ir lineārās nevienādības, kas ir nevienādība, kas diferencē izteiksmes vai nu ar mazāk nekā, vai vienāds ar, mazāk nekā, vai lielāks nekā, vai vienāds ar, lielāks nekā. Tā ir tāda, ka, ja nevienādību aizstāsim ar vienādības sakarību, tad rezultāts būs lineāra vienādība.
- Otrais ir nevienādību kombinācijas, kas ir, lai apmierinātu nevienādības, jums ir jābūt skaitlim risinājumu kopās, lai skaitļi apmierinātu nevienādības būs vērtības krustojumā divu risinājumu kopu.
- Trešais ir nevienādības, kas ietver absolūtās vērtības, kas nozīmē, ka vērtības var pārformulēt kā nevienādību kombinācijas, kas ietver absolūtās vērtības.
- Ceturtais sauc par polinomu nevienādības nozīmē, ka tas ir nepārtraukts, tas nozīmē, ka to grafiki nav nekādu lēcienu vai pārtraukumu.
- Pēdējais, bet ne mazāk svarīgs, ir racionālās nevienādības, kas nozīmē, ka tā ir viena polinoma forma, ko dala ar polinomu. Citiem vārdiem sakot, racionālo funkciju grafikos nav ne pārrāvumu, ne arī attēlojumu pie saucēja nulles.
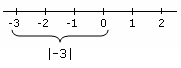
Absolūtā vērtība Piemērs, kas parāda absolūto vērtību
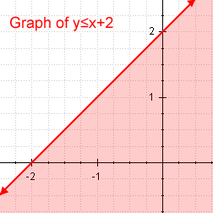
Lineārā nevienlīdzība Lineārās nevienlīdzības piemērs
Četri veidi, kā atrisināt nevienādības
Ir četri veidi, kā atrisināt kvadrātvienādojumus:
- Pirmais noteikums ir, ka abās pusēs ir jāpieskaita vai jāatņem viens un tas pats skaitlis.
- Otrs noteikums ir tāds, ka jums ir jāpārvieto puses un jāmaina nevienlīdzības zīmes novietojums.
- Trešais noteikums ir tāds, ka jums ir jāreizina.
- Ceturtais noteikums ir dalīt vienu un to pašu pozitīvo vai negatīvo skaitli abās pusēs. Taču to var izmantot tikai vieglu nevienādību uzdevumos.
Turklāt nevienlīdzības atrisināšanai būs nepieciešami divi soļi. Pirmais ir vienkāršošana, izmantojot saskaitīšanas vai atņemšanas savstarpējo attiecību. Otrais solis ir vienkāršot vēl vairāk, izmantojot reizināšanas vai dalīšanas savstarpējo attiecību. Ja reizināt vai dalīt nevienādību ar negatīvu skaitli, atcerieties, ka nevienādības simbols ir jāpagriež.

nevienlīdzības reizināšanas piemērs

Piemērs nevienādību saskaitīšanai.
Nevienādību risināšanas piemēri
Nevienlīdzība ir matemātisks apgalvojums, kas izskaidro, ka divas vērtības nav vienādas un atšķirīgas. Vienādojums ab nozīmē, ka a nav vienāds ar b. Nevienādība ir tāda pati kā jebkurš vienādojums, bet vienīgā atšķirība ir tā, ka nevienādībā neizmanto vienādības zīmi, tā vietā izmanto simbolus. Nevienādība b>a nozīmē, ka b ir lielāks par a. Ātruma ierobežojumi, atzīme un citi izmanto nevienādību, lai tos izteiktu.
Risinot nevienlīdzību, personai ir nepieciešams patiess apgalvojums. Ja nevienādību dala vai reizina ar negatīvu skaitli abās pusēs, apgalvojums ir nepatiess. lai apgalvojums būtu pareizs ar negatīvu skaitli, ir jāmaina simbols, lai apgalvojums būtu pareizs. Ja skaitlis ir pozitīvs skaitlis, nav nepieciešams apgriezt simbolu. Nevienādība ir domāta tam, lai apgalvojums būtu patiess.
Piemēram, sāciet ar patieso apgalvojumu -6y<-12. Ja abas malas dalām ar -6, rezultāts būs y< 2. Šajā apgalvojumā simbols ir jāmaina, lai būtu patiess apgalvojums, y>2 ir pareizā atbilde. Skaitļu rindā (sk. 2. attēla nevienādību) slēgts iekrāsots aplis norāda, ka tas ir iekļauts atrisinājuma kopa. Atvērts aplis norāda, ka tas nav iekļauts risinājumu kopa.
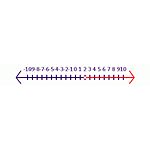
Nevienlīdzība 2 Risinājums vienādojumam -6y<-12
Saistītās lapas
- Vienlīdzība (matemātika)
- Vienādojums
Jautājumi un atbildes
J: Ko nozīmē "a < b"?
A: Tas nozīmē, ka a ir mazāks par b.
J: Ko nozīmē "a > b"?
A: Tas nozīmē, ka a ir lielāks par b.
J: Ko nozīmē "a ≥ b"?
A: Tas nozīmē, ka a nav mazāks par b, t. i., tas ir, tas ir vai nu lielāks, vai vienāds ar b.
J: Ko nozīmē "a ≤ b"?
A: Tas nozīmē, ka a nav lielāks par b, vai tas ir mazāks vai vienāds ar b.
J: Kā nevienlīdzību var izmantot matemātikā?
A: Nevienādību var izmantot, lai nosauktu apgalvojumu, ka viena izteiksme ir mazāka, lielāka, nav mazāka vai nav lielāka par otru.
Meklēt