Slīdrata lineāls (logaritmiskais lineāls) — vēsture, darbība un pielietojums
Atklāj slīdrata (logaritmiskā) lineāla vēsturi, darbības principus un praktisko pielietojumu inženierijā, aviācijā un finansēs — no Napīra idejām līdz kabatas kalkulatora laikmetam.
Slīdrata lineāls (bieži saukts par slide rule, sarunvalodā arī slipstick) ir mehānisks analogais dators, kas izmanto logaritmiskas skalas, lai ātri veiktu reizināšanu, dalīšanu un daudzas citās zinātniskās un inženiertehniskās operācijas. Parasti slīdratu izmanto reizināšanai un dalīšanai, kā arī tādām "zinātniskām" funkcijām kā saknes, logaritmi un trigonometrija, bet to parasti neizmanto saskaitīšanai vai atņemšanai.
Uzbūve un darbības princips
Tipiskam slīdrata lineālam ir fiksētas galvenās (parasti apakšējā) skala, pārvietojama sliede ar otru skalu un pārejas rādītājs — skaidrs slīdnis ar matiņa līniju (cursor). Skalu izvietojums ir logaritmisks: attālums no nulles atbilst skaitļa logaritmam. Reizināšana tiek veikta, pievienojot attālumus (logaritmus) — praktiski sakot, novietojot slēdzi tā, lai attiecīgā vērtība sakristu ar uzstādīto bāzi, un nolasot rezultātu zem rādītāja.
Galvenās skalu grupas
- C un D — visbiežāk lietotās skalas reizināšanai un dalīšanai.
- A un B — kvadrātu un kvadrātsakņu aprēķiniem.
- K — kubu un kubsakņu aprēķiniem.
- L — dekadiskie logaritmi (lietderīgi, lai atrastu logaritma daļu jeb mantisu).
- CI, DI — inversās (apgrieztās) skalas ērtākai dalīšanai vai inversu atrašanai.
- S, T, ST — trigonometriskās skavas (sinuss, tangens un maziem leņķiem izmantojama ST).
- LL (log-log) — eksponenciālām un polārfunkcijām, izmanto, lai strādātu ar mainīgām bāzēm un lieliem diapazoniem.
Tipi un materiāli
Ir daudzi slīdratu veidi: lineārie ( taisni ), apaļie (apļveida) un cilindriskie (garas cilindriskās skalas). Apaļie un cilindriskie lineāli samazina "beigu efektu" un var dot lielāku precizitāti uz īsāka fiziska garuma ierīces. Par materiāliem izmanto koku (bieži pārklātu ar celluloidu), plastmasu, alumīniju un vara sakausējumus. Slīdratu ražotāji, kas ieguvuši atpazīstamību, ir, piemēram, Keuffel & Esser, Faber‑Castell un Pickett (šo konkrēto nosaukumu pieminēšana nav saistīta ar ārējām saitēm šajā rakstā).
Vēsture
1600. gadā Viljams Ohtreds un citi izstrādāja slīdmašīnas pirmās formas — idejas pamatā bija Džona Napīra darbs par logaritmiem, kas parādīja, ka reizināšana var tikt pārvērsta par saskaitīšanu. Pirms tika izstrādāti elektroniskie kalkulatori, slīdrata lineāli bija visbiežāk izmantotais instruments zinātnē un inženierzinātnēs. To izmantošana turpināja pieaugt 20. gadsimta 50. un 60. gados, pat tad, kad pakāpeniski tika ieviestas digitālās skaitļošanas ierīces. Taču ap 1974. gadu kabatas kalkulators padarīja slīdrata lineālus lielā mērā novecojušus, un lielākā daļa ražotāju pameta šo nozari.
Pielietojumi un specializētie lineāli
Slīdrata lineālus izmantoja un joprojām izmanto tādās jomās kā inženierija, fizikā, ķīmijā, navigācijā un aviācijā. Ir izgatavoti speciāli slīdrati ar papildu skalām, paredzēti konkrētām nozarēm — piemēram, aviācijā izmanto specializētus lidojumu kalkulatorus un aviācijā orientētus rīkus (E6B tipa diskus), kā arī finanšu aprēķinos pielāgotus lineālus finansēs ar procentu, procentu punktu un vērtspapīru aprēķinu skalām.
Kā lasīt un veikt pamata darbības
Vienkāršs reizināšanas piemērs (2 × 3 = 6):
- Noliekiet slīdni tā, lai skaitļa 1 uz skalas C sakristu ar skaitli 2 uz skalas D.
- Uz skalas C atrodiet 3 un zem tā uz skalas D nolasiet rezultātu — tas būs aptuveni 6.
Dalīšana notiek pretējā secībā — novietojot dalāmo uz skalu D pret dalītāja vērtību uz skalas C un nolasot zem rādītāja. Desmitu vietu (dekadisko punktu) jānosaka atsevišķi, jo slīdrats rāda tikai skaitļa mantisu (šeit noder L skala un pieredze).
Precizitāte un ierobežojumi
- Precizitāte ir ierobežota ar skalu garumu un gradējuma blīvumu: parasti 3–4 nozīmīgas zīmes uz standarta 25 cm (10") lineāla; garāki vai cilindriski modeļi var dot 4–6 zīmju precizitāti.
- Slīdratu nav ērti izmantot ar ļoti lieliem precizitātes prasībām vai ar operācijām, kas prasa precīzu saskaitīšanu/atņemšanu — šīm darbībām labāk der digitālie rīki.
- Nav automātiskas desimālo vietu noteikšanas — lietotājam pašam jāseko mantisas novietojumam.
Uzturēšana un kopšana
Slīdratu glabāšana sausā vietā, izvairīšanās no tiešiem saules stariem un spēcīgiem šķīdinātājiem (kuri var bojāt celluloid pārklājumus) pagarina ierīces dzīvi. Ja nepieciešams tīrīt, izmanto mīkstu drānu un nelielu daudzumu viegla šķidruma (piem., alkohola) tikai metāla vai plastmasas detaļām, uzmanīgi izvelkot slidendā ritenīša stiprinājumus.
Slīdrata mantojums
Slīdrata lineāls atstājis lielu ietekmi uz mācīšanu un inženiertehnisko praksi 19. un 20. gadsimtā. Lai gan mūsdienās tas lielākoties ir aizstāts ar elektroniskajiem kalkulatoriem un datorprogrammām, kolekcionāri, muzeji un tehnoloģiju entuziasti turpina saglabāt, restaurēt un demonstrēt dažādus vēsturiskos un retus modeļus. Slīdrats joprojām mācāms kā noderīgs instruments, lai saprastu logaritmisko skalu darbību un aprēķinu ideju aiz reizināšanas kā summa.

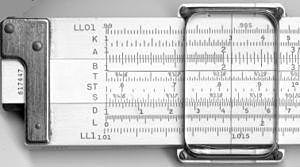
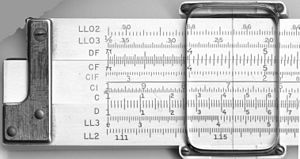
Tipisks desmit collu studentu slīdņa mērvienība (Pickett N902-T simplex trig)

Slaidu mērvienība, kas novietota tā, lai reizinātu ar 2. Katrs skaitlis D (apakšējā) skalā ir divkāršots skaitlim virs tā C (vidējā) skalā.
Pamatjēdzieni
Savā visvienkāršākajā formā bīdāmajā lineā tiek izmantotas divas logaritmiskās skalas, kas ļauj ātri reizināt un dalīt skaitļus. Veicot šīs parastās darbības uz papīra, tās var būt laikietilpīgas un kļūdainas. Sarežģītāki diapozitīvi ļauj veikt citus aprēķinus, piemēram, kvadrātsakņu, eksponentu, logaritmu un trigonometrisko funkciju aprēķinus.
Matemātiskos aprēķinus veic, saskaņojot zīmi uz slīdošās centrālās sloksnes ar zīmi uz vienas no fiksētajām sloksnēm. Pēc tam var novērot citu zīmju relatīvo stāvokli. Skaitļi, kas sakārtoti ar zīmēm, norāda aptuveno reizinājuma, reizinātāja vai cita aprēķinātā rezultāta vērtību.
Lietotājs nosaka decimālpunkta atrašanās vietu rezultātā, pamatojoties uz aplēsēm. Lai sekotu līdzi decimālpunkta atrašanās vietai formālākos aprēķinos, izmanto zinātnisko apzīmējumu. Saskaitīšanas un atņemšanas soļus aprēķinā parasti veic mentāli vai uz papīra, nevis uz diapozitīva.
Lielākajai daļai bīdāmo noteikumu ir trīs vienāda garuma lineārās sloksnes. Lentes ir izkārtotas paralēli un savstarpēji savienotas tā, ka centrālo lenti var pārvietot gareniski attiecībā pret pārējām divām. Divas ārējās sloksnes ir nostiprinātas tā, ka to relatīvā pozīcija nemainās.
Dažiem bīdāmajiem lineāliem ("duplex" modeļi) skalas ir abās lineāla un slīdlentes pusēs, citiem - vienā ārējās sloksnes pusē un abās slīdlentes pusēs, bet vēl citiem - tikai vienā pusē ("simplex" lineāli). Slīdošo kursoru ar vertikālo izlīdzināšanas līniju izmanto, lai atrastu atbilstošos punktus uz skalām, kas nav blakus viena otrai vai dupleksa modeļos atrodas otrā lineāla pusē. Kursors var arī reģistrēt starprezultātu jebkurā skalā.

Kursors uz diapozitīva
Slīdņa regulāra izmantošana aprēķiniem
Reizināšana
Logaritms pārveido reizināšanas un dalīšanas darbības saskaitīšanā un atņemšanā saskaņā ar noteikumiem log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} 











Darbības var notikt "ārpus skalas", piemēram, diagrammā iepriekš redzams, ka bīdāmā lineāra augšējā skalas daļā 7 nav novietots virs jebkura skaitļa apakšējā skalas daļā, tāpēc tas nesniedz atbildi uz 2×7. Šādos gadījumos lietotājs var bīdīt augšējo skalu pa kreisi, līdz tās labais indekss sakrīt ar 2, tādējādi reizinot ar 0,2, nevis ar 2, kā parādīts attēlā zemāk:
![]()
Šajā gadījumā slīdņa lietotājam ir jāatceras, ka, lai koriģētu galīgo atbildi, ir attiecīgi jāpielāgo decimāldaļa. Mēs gribējām atrast 2×7, bet tā vietā aprēķinājām 0,2×7=1,4. Tātad patiesā atbilde nav 1,4, bet gan 14. Skaitļa atiestatīšana nav vienīgais veids, kā apstrādāt reizinājumus, kuru rezultātā varētu rasties rezultāti, kas neatbilst skalai, piemēram, 2×7; ir arī dažas citas metodes:
- (1) Izmantojiet divu dekāžu skalas A un B.
- (2) Izmantojiet salocītos svarus. Šajā piemērā iestatiet C kreiso 1 pretī D 2. Novietojiet kursoru uz 7 CF un nolasiet rezultātu no DF.
- (3) Izmantojiet apgriezto skalu CI. Novietojiet 7 uz CI skalas virs 2 uz D skalas un pēc tam nolasiet rezultātu no D skalas zem 1 uz CI skalas. Tā kā 1 atrodas divās vietās CI skalā, viena no tām vienmēr būs skalas iekšpusē.
- (4) Izmantojiet gan CI apgriezto skalu, gan C skalu. Novietojiet CI 2 līdz 1 D skalā un nolasiet rezultātu no D zem 7 C skalā.
Pirmā metode ir viegli saprotama, taču tā ir saistīta ar precizitātes zudumu. Trešās metodes priekšrocība ir tā, ka tā ietver tikai divas skalas.
Nodaļa
Nākamajā attēlā parādīts aprēķins 5,5/2. 2 augšējā skalā ir novietots virs 5,5 apakšējā skalā. Augšējā skalā 1 atrodas virs koeficienta 2,75. Ir vairāk nekā viena metode, kā veikt dalīšanu, bet šeit attēlotajai metodei ir tā priekšrocība, ka galarezultāts nevar būt ārpus skalas, jo ir iespēja izvēlēties, vai izmantot 1 abos galos.

Citas darbības
Papildus logaritmiskām skalām dažos diapozitīvos mērinstrumentos ir arī citas matemātiskās funkcijas, kas ir kodētas citās palīgskalās. Vispopulārākās bija trigonometriskās skalas, parasti sinusa un tangensa, parastais logaritms (log10) (vērtības logaritma iegūšanai reizinātāja skalā), naturālā logaritma (ln) un eksponenciālā (ex ) skalas. Daži noteikumi ietver Pitagora skalu, lai aprēķinātu trīsstūru malas, un skalu, lai aprēķinātu apļus. Citos ir skalas hiperbolisko funkciju aprēķināšanai. Lineārajos noteikumos skalas un to marķējums ir ļoti standartizēts, un atšķirības parasti ir tikai attiecībā uz to, kuras skalas un kādā secībā ir iekļautas:
| A, B | divu dekāžu logaritmiskās skalas, ko izmanto skaitļu kvadrātsakņu un kvadrātu atrašanai. |
| C, D | vienas dekādes logaritmiskās skalas |
| K | trīs dekāžu logaritmiskā skala, ko izmanto kubisko sakņu un skaitļu kubu atrašanai. |
| CF, DF | C un D skalu "salocītās" versijas, kas sākas no π, nevis no vienādības; tās ir ērtas divos gadījumos. Pirmkārt, ja lietotājs nojauš, ka produkts būs tuvu 10, bet nav pārliecināts, vai tas būs nedaudz mazāks vai nedaudz lielāks par 10, salocītās skalas ļauj izvairīties no iespējas iziet no skalas. Otrkārt, padarot sākumu π, nevis kvadrātsakni no 10, tiek vienkāršota reizināšana vai dalīšana ar π (kā tas parasti notiek dabaszinātņu un inženierzinātņu formulās). |
| CI, DI, DIF | "apgrieztās" skalas, kas iet no labās puses uz kreiso, izmanto, lai vienkāršotu 1/x soļus. |
| S | ko izmanto sinusu un kosinusu noteikšanai D skalā |
| T | ko izmanto, lai atrastu tangentes un kotangentus D un DI skalās. |
| ST, SRT | izmanto mazu leņķu sinusiem un tangentiem un grādu-radiānu konversijai. |
| L | lineārā skala, ko izmanto kopā ar C un D skalu, lai atrastu 10 bāzu logaritmus un 10 reizinājumus. |
| LLn | logaritmu un logaritmu skalu kopums, ko izmanto skaitļu logaritmu un eksponenciālu noteikšanai. |
| Ln | lineārā skala, ko izmanto kopā ar C un D skalu, lai atrastu dabiskos (e bāzes) logaritmus un e x {\displaystyle e^{x}}. |
| ||
| K&E 4081-3 bīdāmā noteikšanas mehānisma skalas priekšpusē un aizmugurē. |
Gilsona 1931. gadā ražotais binārais slaidu lineāls veica saskaitīšanas un atņemšanas funkciju, kas attiecās tikai uz frakcijām.
Saknes un pilnvaras
Pastāv vienas dekādes (C un D), divu dekāžu (A un B) un trīs dekāžu (K) skalas. Lai aprēķinātu x 2 {\displaystyle x^{2}} 
x y {\displaystyle x^{y}}

Trigonometrija
S, T un ST skalas izmanto trigonometriskām funkcijām un trigonometrisko funkciju reizinājumiem, leņķiem grādos. Daudziem diapozitīviem ir S, T un ST skalas, uz kurām ir atzīmēti grādi un minūtes. Tā sauktajos decitrigu modeļos tā vietā izmanto decimāldaļas grādos.
Logaritmi un eksponenti
Logaritmus un eksponentus ar lineāro skalu L atrod, izmantojot lineāro skalu L. Dažiem bīdāmajiem logaritmiem ir Ln skala, kas paredzēta bāzei e.
Ln skalu 1958. gadā izgudroja 11. klases skolnieks Stīvens B. Koens. Sākotnējais nolūks bija ļaut lietotājam izvēlēties eksponentus x (diapazonā no 0 līdz 2,3) Ln skalā un nolasīt ex C (vai D) skalā un e–x CI (vai DI) skalā. Pickett, Inc. tika piešķirtas ekskluzīvas tiesības uz skalu. Vēlāk izgudrotājs uz Ln skalas izveidoja "zīmju" komplektu, lai paplašinātu diapazonu ārpus 2,3 robežas, bet Pickett nekad neiekļāva šīs zīmes nevienā no saviem slaidiem. []
Saskaitīšana un atņemšana
Saskaitīšanas un atņemšanas darbiem parasti neizmanto slīdošos noteikumus, tomēr to ir iespējams izdarīt, izmantojot divus dažādus paņēmienus.
Lai veiktu saskaitīšanu un atņemšanu ar C un D (vai jebkuru citu salīdzināmu skalu), pirmā metode prasa pārveidot uzdevumu par dalīšanas uzdevumu. Saskaitīšanas gadījumā abu mainīgo kvantients plus viens reiz dalītājs ir vienāds to summai:
x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}
Atņemšanas gadījumā abu mainīgo reizinājums mīnus viens mīnus dalītājs ir vienāds ar to starpību:
x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}
Šī metode ir līdzīga saskaitīšanas/izvilkšanas metodei, ko izmanto ātrgaitas elektroniskajās shēmās ar logaritmisko skaitļu sistēmu specializētos datoru lietojumos, piemēram, superdatorā Gravity Pipe (GRAPE) un slēptajos Markova modeļos.
Otrajā metodē tiek izmantota bīdāmā lineārā L skala, kas pieejama dažos modeļos. Saskaitīšanu un atņemšanu veic, bīdot kursoru pa kreisi (atņemšanai) vai pa labi (saskaitīšanai) un pēc tam atgriežot bīdni uz 0, lai nolasītu rezultātu.
Fiziskā konstrukcija
Standarta lineārie noteikumi
Slīpmašīnas garums ir izteikts kā skalu nominālais garums. Visbiežāk sastopamo "10 collu" modeļu skalas patiesībā ir 25 cm garas, jo tās ir izgatavotas saskaņā ar metriskajiem standartiem, lai gan daži noteikumi piedāvā nedaudz pagarinātas skalas, lai vienkāršotu manipulācijas, ja rezultāts ir pārpildīts. Kabatas noteikumi parasti ir 5 collas. Pāris metrus garus modeļus pārdeva, lai tos varētu iekārt klasēs mācību nolūkos. [1]
Parasti dalījumi iezīmē skalu ar divu zīmīgo ciparu precizitāti, un lietotājs novērtē trešo ciparu. Dažiem augstas klases diapozitīviem mērinstrumentiem ir palielinoši kursori, kas padara marķējumus vieglāk saskatāmus. Šādi kursori var efektīvi dubultot rādījumu precizitāti, ļaujot 10 collu slīpraktikam kalpot tikpat labi kā 20 collu slīprakstam.
Ir izstrādātas dažādas citas ērtības. Trigonometriskie mērogi dažkārt tiek marķēti divējādi, melnā un sarkanā krāsā, ar papildu leņķiem, tā sauktajā "Darmštates" stilā. Dubultie bīdāmie lineāli bieži dublē dažas skalas uz aizmugures. Skalas bieži tiek "sadalītas", lai iegūtu lielāku precizitāti.
Tika izgudroti specializēti bīdāmie noteikumi dažādiem inženierzinātņu, uzņēmējdarbības un banku darbības veidiem. Tajos bieži vien parastie aprēķini bija tieši izteikti kā īpašas skalas, piemēram, aizdevumu aprēķini, optimālie pirkuma daudzumi vai konkrēti inženiervienādojumi. Piemēram, uzņēmums Fisher Controls izplatīja pielāgotu diapozitīvu, kas bija pielāgots vienādojumu risināšanai, kurus izmantoja, lai izvēlētos atbilstoša izmēra rūpnieciskos plūsmas regulēšanas vārstus. []
Apļveida bīdāmie noteikumi
Cirkulārie diapozitīvi ir divu veidu - ar diviem kursoriem (pa kreisi) un ar kustīgu disku un vienu kursoru (pa labi). Divu kursoru versijās reizināšanu un dalīšanu veic, saglabājot nemainīgu leņķi starp kursoriem, kad tie tiek pagriezti ap ripu. Viena kursora versija darbojas vairāk kā standarta bīdāmā mērierīce, izmantojot atbilstošu skalu izlīdzināšanu.
Apļveida slīdņa galvenā priekšrocība ir tā, ka instrumenta garākais izmērs tika samazināts aptuveni 3 reizes (t. i., par π). Piemēram, 10 cm cirkulārā skalas ārējā skala būtu ar maksimālo precizitāti, kas vienāda ar 30 cm parastā diapozitīva skalu. Apļveida bīdāmie mērogi arī novērš aprēķinus "ārpus skalas", jo mērogi ir konstruēti tā, lai "apvītu"; tie nekad nav jāpārorientē, ja rezultāti ir tuvu 1,0 - mērogi vienmēr ir saskaņā ar skalu. Tomēr necikliskajiem ne-spirālveida skalām, piemēram, S, T un LL, skalas garums ir saīsināts, lai atvēlētu vietu gala malām.
Cirkulārie bīdāmie regulatori ir mehāniski izturīgāki un kustīgākie, taču to skalas izlīdzināšanas precizitāte ir atkarīga no centrālā šarnīra centrēšanas; neliela 0,1 mm novirze no šarnīra centra var radīt 0,2 mm izlīdzināšanas kļūdu sliktākajā gadījumā. Tomēr šarnīrs novērš skalas virsmas un kursoru saskrāpēšanu. Vislielākās precizitātes skalas ir novietotas uz ārējiem gredzeniem. Augstas klases apļveida regulās sarežģītākām operācijām, piemēram, logaritmu skalas, izmanto nevis "dalītās" skalas, bet gan spirālveida skalas. Vienam astoņu collu augstākās klases cirkulārajam regulējumam bija 50 collu spirālveida logaritmu skala.
Galvenie apļveida bīdāmo noteikumu trūkumi ir grūtības noteikt figūru atrašanās vietu rotējošā diskā un ierobežots skalu skaits. Vēl viens apaļo bīdāmo riņķu trūkums ir tas, ka mazāk svarīgas skalas atrodas tuvāk centram un to precizitāte ir zemāka. Lielākā daļa skolēnu iemācījās izmantot lineāros diapozitīvos slaidus, un neatrada iemeslu, lai tos nomainītu.
Pasaulē joprojām ikdienā tiek izmantots viens no slaidu mērinstrumentiem - E6B. Tas ir apaļais bīdāmo noteikumu modelis, kas pirmo reizi tika radīts pagājušā gadsimta 30. gados lidmašīnu pilotiem, lai palīdzētu veikt aprēķinus pēc nulles. Ar uz rāmja uzdrukāto skalu palīdzību tas palīdz veikt arī tādus dažādus uzdevumus kā laika, attāluma, ātruma un temperatūras vērtību, kompasa kļūdu un degvielas patēriņa aprēķināšana. Tā sauktais "lūgšanu ritenis" joprojām ir pieejams lidojuma veikalos, un to joprojām plaši izmanto. Lai gan GPS ir samazinājis "dead reckoning" izmantošanu aeronavigācijā un daudzas tā funkcijas ir pārņēmuši portatīvie kalkulatori, E6B joprojām plaši izmanto kā galveno vai rezerves ierīci, un lielākā daļa lidojumu skolu pieprasa, lai to studenti to apgūtu zināmā līmenī.
1952. gadā Šveices pulksteņu kompānija Breitling laida klajā pilota rokas pulksteni ar integrētu apaļu slīdni, kas specializēts lidojumu aprēķiniem: Breitling Navitimer. Navitimer apļveida ciparnīcā, ko Breitling dēvēja par "navigācijas datoru", bija gaisa ātruma, pacelšanās/nolaišanās ātruma/laika, lidojuma laika, attāluma un degvielas patēriņa funkcijas, kā arī kilometru-jūras jūdžu un galonu-litru degvielas daudzuma pārrēķina funkcijas.
Materiāli
Tradicionāli bīdāmie lineāli tika izgatavoti no cietas koksnes, piemēram, sarkankoka vai buksusa, ar stikla un metāla kursoriem. Vismaz viens augstas precizitātes instruments bija izgatavots no tērauda.
1895. gadā japāņu uzņēmums Hemmi sāka ražot bambusa bīdāmos noteikumus, kuru priekšrocība bija izmēru stabilitāte, izturība un dabiskā pašeļļošanās. Zviedrijā bambusa bīdāmos noteikumus ieviesa 1933. gada septembrī [2], bet Vācijā, iespējams, tikai nedaudz agrāk. Mērogus izgatavoja no celuloīda vai plastmasas. Vēlāk slīdni tika izgatavoti no plastmasas vai alumīnija, kas nokrāsots ar plastmasu. Vēlākie kursori bija no akrila vai polikarbonāta, kas slīdēja uz teflona gultņiem.
Visiem augstākās kvalitātes slaidiem bija iegravēti skaitļi un skalas, kas pēc tam tika aizpildīti ar krāsu vai citiem sveķiem. Krāsoti vai apdrukāti bīdāmie noteikumi tika uzskatīti par sliktākiem, jo marķējums varēja nolietoties. Tomēr Pickett, iespējams, Amerikas veiksmīgākais diapozitīvu uzņēmums, izgatavoja visas apdrukātās skalas. Augstākā labuma bīdāmo noteikumu komplektā bija atjautīgi fiksatori, lai likums nejauši nesadalītos, un buferi, kas pasargāja skalas un kursoru no berzes uz galda virsmām. Ieteicamā attīrīšanas metode iegravētiem marķējumiem ir viegli noslaucīt ar tērauda vati. Krāsotām bīdāmajām normām un tiem, kam ir vājš prāts, izmantojiet atšķaidītu komerciālu logu tīrīšanas šķidrumu un mīkstu drānu.

Pickett riņķveida bīdāmā mērierīce ar diviem kursoriem. (4,25 collas / 10,9 cm diametrs) Reversā ir papildu skala un viens kursors.

Vienkāršs apaļš bīdāms regulators, ko ražojusi Concise Co., Ltd., Tokija, Japāna, tikai ar apgriezto, kvadrātisko un kubisko skalu. Uz otrā pusē ir ērts saraksts ar 38 metrisko/imperiālo pārrēķina koeficientu sarakstu.

Breitling Navitimer rokas pulkstenis ar apaļu bīdāmo noteikumu
Vēsture
Slīdni izgudroja aptuveni 1620.-1630. gadā, neilgi pēc tam, kad Džons Napjērs publicēja logaritma jēdzienu. Edmunds Gunters no Oksfordas izstrādāja skaitļošanas ierīci ar vienu logaritmisko skalu, kuru, izmantojot papildu mērinstrumentus, varēja izmantot reizināšanai un dalīšanai. Pirmo šīs skalas aprakstu 1624. gadā Parīzē publicēja angļu matemātiķis Edmunds Vingate (Edmund Wingate, ap 1593 - 1656) grāmatā "L'usage de la reigle de proportion en l'arithmetique & geometrie" ("Proporcijas mērauklas izmantošana aritmētikā un ģeometrijā"). Grāmatā ir dubulta skala, kuras vienā pusē ir logaritmiskā skala, bet otrā - tabulārā skala. 1630. gadā Viljams Oughtreds no Kembridžas izgudroja apaļu bīdāmo noteikumu, bet 1632. gadā viņš apvienoja divus Guntera noteikumus, ko turēja kopā ar rokām, lai izveidotu ierīci, kas ir atpazīstama kā mūsdienu bīdāmo noteikumu. Tāpat kā viņa laikabiedrs Kembridžā Īzaks Ņūtons, Oughtreds savas idejas privāti mācīja saviem studentiem, bet kavējās ar to publicēšanu, un, tāpat kā Ņūtons, viņš iesaistījās vētrainā strīdā par prioritāti ar savu kādreizējo studentu Ričardu Delamainu un Vingatesa iepriekšējām prasībām. Oughtreda idejas tika publiskotas tikai viņa skolnieka Viljama Forstera publikācijās 1632. un 1653. gadā.
1677. gadā Henrijs Koggeshols (Henry Coggeshall) izgatavoja divu pēdu salokāmu noteikumu kokmateriālu mērīšanai, ko sauca par Koggeshalla slīdošo noteikumu. Viņa izstrādātais dizains un rīka pielietojums piešķīra slīpraktiķim mērķi ārpus matemātiskās izpētes.
1722. gadā Vorners ieviesa divu un trīs dekāžu skalas, bet 1755. gadā Everards pievienoja apgriezto skalu; bīdāmo mērauklu, kurā ir visas šīs skalas, parasti sauc par "daudzfāžu" mērauklu.
1815. gadā Pīters Rogets izgudroja logaritma logaritma logaritmu, kurā bija logaritma logaritma logaritma skala. Tas ļāva lietotājam tieši veikt aprēķinus ar saknēm un eksponentiem. Tas bija īpaši noderīgi, kad vajadzēja aprēķināt daļskaitļus.
Mūsdienu forma
Mūsdienīgāko formu 1859. gadā izveidoja franču artilērijas leitnants Amēde Manheims, "kuram paveicās, ka viņa noteikumus izgatavoja valsts mēroga firma un ka tos pieņēma Francijas artilērija". Aptuveni tajā laikā, kad inženierzinātnes kļuva par atzītu profesionālu darbību, Eiropā plaši sāka izmantot slīdošos noteikumus. Amerikas Savienotajās Valstīs tie kļuva plaši izplatīti tikai 1881. gadā, kad Edvīns Tačers (Edwin Thacher) ieviesa cilindrisko noteikumu. Divpusējo noteikumu izgudroja Viljams Kokss 1891. gadā, un to ražoja Ņujorkas uzņēmums Keuffel and Esser Co.
Astronomiskajam darbam bija nepieciešami arī smalki aprēķini, un 19. gadsimtā Vācijā vienā observatorijā izmantoja aptuveni 2 metrus garu tērauda slīdni. Tam bija pievienots mikroskops, kas nodrošināja precizitāti līdz sešām zīmēm aiz komata.
Otrā pasaules kara laikā spridzinātāji un navigatori, kuriem bija nepieciešami ātri aprēķini, bieži izmantoja specializētus bīdāmos noteikumus. Viens no ASV Jūras kara flotes birojiem izstrādāja vispārīgu bīdāmo noteikumu "šasiju" ar alumīnija korpusu un plastmasas kursoru, kurā īpašiem aprēķiniem varēja ievietot celuloīda kartes (apdrukātas no abām pusēm). Šis process tika izgudrots, lai aprēķinātu lidmašīnu darbības rādiusu, degvielas patēriņu un augstumu, un pēc tam tika pielāgots daudziem citiem mērķiem.
Pagājušā gadsimta 50. un 60. gados slaidu mērvienība bija inženiera profesijas simbols (līdzīgi kā stetoskops simbolizē mediķa profesiju).[] Vācu raķešu zinātnieks Vernhers fon Brauns (Wernher von Braun), pēc Otrā pasaules kara pārceļoties uz ASV, lai strādātu pie amerikāņu kosmosa programmas, paņēma līdzi divus 30. gadu Nestler slaidu noteikumus. Visu savu mūžu viņš nekad nav izmantojis citas kabatas skaitļošanas ierīces; slīpraksti viņam lieliski noderēja, lai ātri aprēķinātu raķešu konstrukcijas parametrus un citus skaitļus. Saskaņā ar reklāmu uz Pickett's N600 slaidu likmju kastēm [3] Pickett's N600 slaidu likmju kastes [3] alumīnija Pickett zīmola slaidu likumi tika izmantoti piecās Apollo kosmosa misijās, tostarp uz Mēnesi.
Daži inženierzinātņu studenti un inženieri nēsāja desmit collu slīpmašīnas jostas kabatās, un pat 20. gadsimta 70. gadu vidū tas bija ierasta parādība studentu pilsētiņās. Studenti varēja arī turēt desmit vai divdesmit collu izmēru lineālu precīzam darbam mājās vai birojā, bet pie sevis nēsāt piecu collu kabatas bīdāmo lineālu.
2004. gadā izglītības pētnieki Deivids B. Šērs un Dīns K. Nataro (Dean C. Nataro) izstrādāja jauna veida slaidu noteikumu, kas balstīts uz prosthaferezi - algoritmu ātrai produktu aprēķināšanai, kas radies pirms logaritmu ieviešanas. Tomēr praktiskā interese par šāda modeļa izgatavošanu ir bijusi neliela, pārsniedzot sākotnējo prototipu. [4]
Samazinājums
Slīpmašīnas nozīme sāka mazināties, kad 20. gadsimta 50. gados elektroniskie datori, kas bija jauns, bet ļoti deficīts resurss, 60. gados kļuva plaši pieejami tehniskajiem darbiniekiem. Pēc Fortran ieviešanas 1957. gadā datori kļuva praktiski izmantojami neliela izmēra matemātisku uzdevumu risināšanai. IBM ieviesa virkni pieejamāku datoru - IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965), kas bija paredzēti zinātnes un inženierzinātņu tirgum. Džona Kemenija (John Kemeny) BASIC programmēšanas valoda (1964) atviegloja datoru lietošanu studentiem. DEC PDP-8 minikompjūters tika ieviests 1965. gadā.
Datori mainīja arī aprēķinu raksturu. Ar bīdāmajiem principiem liels uzsvars tika likts uz algebru, lai izteikumus pārveidotu aprēķiniem vispiemērotākajā formā. Lai vienkāršotu aprēķinu, diapozitīvu lietotāji vienkārši aproksimēja vai atteicās no maziem izteicieniem. Fortran ļāva ievadīt sarežģītas formulas no mācību grāmatām, neveicot pārformulēšanu. Skaitliskā integrācija bieži vien bija vienkāršāka nekā mēģinājumi atrast slēgtas formas risinājumus sarežģītiem uzdevumiem. Jaunais inženieris, kas lūdz datora laiku, lai atrisinātu problēmu, kuru varēja atrisināt ar dažiem slīpraksta vilcieniem, kļuva par humoristisku klišeju. Daudzos datoru centros pie sienas bija piekārts ierāmēts diapozitīvs ar uzrakstu "Avārijas gadījumā izsists stikls".
Vēl viens solis ceļā uz diapozitīvu aizvietošanu ar elektroniku bija elektronisko kalkulatoru izstrāde zinātniskai un inženiertehniskai lietošanai. Pirmais no tiem bija Wang Laboratories LOCI-2, kas tika ieviests 1965. gadā un kas reizināšanai un dalīšanai izmantoja logaritmus, un Hewlett-Packard HP-9100, kas tika ieviests 1968. gadā. HP-9100 papildus eksponentiem un logaritmiem bija arī trigonometriskās funkcijas (sin, cos, tan). Tajā tika izmantots CORDIC (koordinātu rotācijas digitālais dators) algoritms, kas ļauj aprēķināt trigonometriskās funkcijas, izmantojot tikai nobīdes un saskaitīšanas darbības. Šī metode atviegloja arvien mazāku zinātnisko kalkulatoru izstrādi.
Pēdējā nagla bīdāmā skaitļa zārkā bija kabatas izmēra zinātnisko kalkulatoru ieviešana, no kuriem pirmais bija Hewlett-Packard HP-35, kas tika ražots 1972. gadā. Šādus kalkulatorus sāka dēvēt par "slaidu rullīša" kalkulatoriem, jo tie varēja veikt lielāko daļu vai visas funkcijas, ko veica slaidu rullītis. Vairumam studentu pat šie kalkulatori, kuru cena bija vairāki simti dolāru, šķita dārgi. Lai gan profesionālie diapozitīvi varēja būt arī diezgan dārgi, aptiekās bieži vien varēja iegādāties vienkāršus plastmasas modeļus par mazāk nekā 20 ASV dolāriem. Taču 1975. gadā četru funkciju elektroniskos kalkulatorus varēja iegādāties par mazāk nekā 50 ASV dolāriem. Līdz 1976. gadam TI-30 piedāvāja zinātnisko kalkulatoru par mazāk nekā 25 ASV dolāriem. Pēc šī laika, kad mazie zinātniskie kalkulatori kļuva pieejami par pieņemamu cenu, slaidu likmju tirgus strauji izsīka.

Viljams Ohtreds (1575-1660), riņķveida slīpveida mērvienības izgudrotājs.

Inženieris, kas izmanto bīdāmo noteikumu. Fonā ir mehāniskais kalkulators.

TI-30
Priekšrocības
- Slaidu likums mēdz mazināt "viltus precizitātes" un nozīmīguma kļūdu. Tipiskā precizitāte, kas ir pieejama slīpmašīnas lietotājam, ir aptuveni trīs precizitātes vietas. Tas labi atbilst lielākajai daļai datu, kas pieejami ievadīšanai inženiertehniskajās formulās. Ja izmanto modernu kabatas kalkulatoru, precizitāte var būt norādīta līdz septiņām vai vairāk zīmēm aiz komata, lai gan patiesībā rezultāti nekad nevar būt precīzāki par pieejamajiem ievaddatiem.
- Slīdneimeris prasa nepārtrauktu rezultātu lieluma secības novērtēšanu. Ar diapozitīvu 1,5 × 30 (kas ir 45) parādīs tādu pašu rezultātu kā 1 500 000 × 0,03 (kas ir 45 000). Inženierim ir pastāvīgi jānosaka rezultātu pamatotība, ko var zaudēt, ja skaitļi tiek neuzmanīgi ievadīti datorprogrammā vai kalkulatorā.
- Veicot reizinājumu vai dalīšanu ar vienu un to pašu skaitli, atbildi bieži vien var noteikt, vienkārši paskatoties uz bīdāmo mērauklu, bez jebkādām manipulācijām. Tas var būt īpaši noderīgi, aprēķinot procentuālos daudzumus, piemēram, testa rezultātu, vai salīdzinot cenas, piemēram, dolāros par kilogramu. Ar slīdrata palīdzību var veikt vairākus ātruma, laika un attāluma aprēķinus ar vienu acu uzmetienu.
- Slīdneimeris nav atkarīgs no elektrības.
- Slīdneklis ir viegli atkārtojama tehnoloģija. Kompetents amatnieks no vienkāršiem materiāliem, izmantojot ar rūpniecību nesaistītus procesus, var uzbūvēt vēl vairāk slīpraktiķu no dotā parauga.
- Slaidu noteikumi ir ļoti standartizēti, tāpēc, pārejot uz citu noteikumu, nav nepieciešams neko mācīties no jauna.
- Slīdgriezes regulatori ir universāli, un ar tiem var strādāt situācijās un vidē, kur lietotājam var būt ierobežotas veiklības (piemēram, tāpēc, ka nepieciešami aizsargcimdi). Turpretī ar kalkulatoru šādās situācijās var būt sarežģīti strādāt - maz ticams, ka ar slīprakstu varētu rasties kļūda, kas līdzinātos kļūdai, kas rodas, kļūdaini nospiežot nepareizu pogu uz kalkulatora.
- Slaidu noteikumus var izgatavot no kartona vai papīra. Daudzas no kartona izgatavotas bezmaksas diagrammas vai specializētas aprēķina ierīces patiesībā ir specializēti lineāri vai apaļi bīdāmie noteikumi.
Viena no priekšrocībām, ko sniedz slīpmašīnas un elektroniskā kalkulatora lietošana, ir tā, ka svarīgu aprēķinu var pārbaudīt, veicot to ar abiem; tā kā abi instrumenti ir tik atšķirīgi, ir maza iespēja kļūdīties divas reizes.
Trūkumi
- Kļūdas var rasties mehāniskas neprecizitātes dēļ.
- Aprēķiniem, izmantojot diapozitīvu, ir ierobežota precizitāte, jo to analogās ieejas un izejas ir ierobežotas. Turpretī diskrētās skaitliskās ievades un elektronisko operāciju ar peldošo komatu dēļ pat pieticīgu mūsdienu kalkulatoru izšķirtspēja ir vismaz seši zīmīgie skaitļi.
Saistītās lapas
Jautājumi un atbildes
J: Kas ir diapozitīvs?
A.: Slīpraksts ir mehānisks analogs dators, ko galvenokārt izmanto reizināšanai un dalīšanai, kā arī zinātniskām funkcijām, piemēram, saknēm, logaritmiem un trigonometrijai.
J: Kādi ir dažādi diapozitīvu noteikumu veidi?
A: Slīdneši var būt lineāri vai apaļi, un tiem var būt standartizēts marķējumu vai skalu kopums, ko izmanto matemātiskiem aprēķiniem. Dažas speciālas lietošanas bīdāmās bildes ir izgatavotas aviācijai vai finansēm ar īpašām skalu skalu šādām vajadzībām.
J: Kurš izgudroja slīdni?
A: Slīdratu izgudroja Viljams Oughtreds, pamatojoties uz Džona Napjēra darbu par logaritmiem.
J: Kad tika izstrādāti elektroniskie kalkulatori?
A: Elektroniskie kalkulatori tika izstrādāti pirms 1970. gadiem, bet aptuveni 1974. gadā kabatas kalkulators padarīja slīpmašīnu par lielā mērā novecojušu.
J: Ko cilvēki visbiežāk izmantoja dabaszinātnēs un inženierzinātnēs, pirms tika izstrādāti elektroniskie kalkulatori?
A.: Pirms elektronisko kalkulatoru izstrādes cilvēki zinātnē un inženierzinātnēs visbiežāk izmantoja slīpraktiķi.
Jautājums: Cik ilgi cilvēki turpināja izmantot diapozitīvu pēc tam, kad tika ieviestas digitālās skaitļošanas ierīces?
A: Cilvēki turpināja izmantot diapozitīvu pat 50. un 60. gados, kad pakāpeniski tika ieviestas digitālās skaitļošanas ierīces.
Meklēt