Pī
Pi (jeb π) ir matemātiska konstante. Tā ir attāluma ap apli attiecība pret apļa diametru. Tas dod skaitli, un šis skaitlis vienmēr ir viens un tas pats. Tomēr šis skaitlis ir diezgan dīvains. Skaitlis sākas ar 3,141592653589793... un turpinās bez gala. Šādus skaitļus sauc par iracionāliem skaitļiem.
Diametrs ir lielākā akorda, ko var ievietot apļa iekšpusē. Tā iet caur apļa centru. Attālumu ap loku sauc par apkārtmēru. Lai gan diametrs un apkārtmērs dažādiem apļiem ir atšķirīgs, skaitlis pi paliek nemainīgs - tā vērtība nekad nemainās. Tas ir tāpēc, ka attiecība starp apkārtmēru un diametru vienmēr ir vienāda.
π = C d {\displaystyle \pi ={\frac {C}{d}}}} 
(pi ir vienāds ar apkārtmēru, kas dalīts ar diametru).
Pi ir bezgalīga skaitļu virkne
Aproksimācija
Pi bieži tiek rakstīts kā π vai grieķu burts π kā saīsinājums. Pi ir arī iracionāls skaitlis, kas nozīmē, ka to nevar rakstīt kā daļskaitli ( a b {\displaystyle a \over b}
), kur 'a' un 'b' ir veseli skaitļi (veseli skaitļi). Tas būtībā nozīmē, ka pi cipari, kas atrodas pa labi no decimāldaļskaitļa, neatkārtojas bezgalīgi, un ka nav iespējams rakstīt precīzu pi vērtību kā skaitli. Pi var tikai tuvināt vai izmērīt līdz vērtībai, kas ir pietiekami tuva praktiskiem mērķiem.
Vērtība, kas ir tuvu pi, ir 3,141592653589793238462643... Parastais pi tuvinājums ir 22 7 {\displaystyle 22 \pārsniedz 7}. 
, kas dod aptuveni 3,14285714. Šī aproksimācija ir 0,04% attālumā no patiesās pi vērtības. Lai gan šis tuvinājums lielākoties ir pieņemams izmantošanai reālajā dzīvē, frakcija 355 113 {\displaystyle 355 \over 113}
ir precīzāka (dod aptuveni 3,14159292), un to var izmantot, ja vajadzīga vērtība, kas tuvāka pi. Datorus var izmantot, lai iegūtu labākus pi tuvinājumus.
2019. gada martā Emma Haruka Iwao aprēķināja pi vērtību līdz 31,4 triljoniem ciparu.
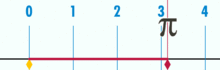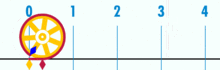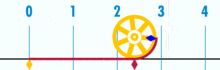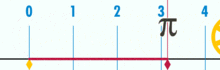
Diagramma, kurā parādīts, kā π var atrast, izmantojot apli ar diametru viens. Šī apļa apkārtmērs ir π.
Vēsture
Pī vērtība bija zināma tādiem senās Indijas matemātiķiem kā Bhaskaracharya un Aryabhatta.
Matemātiķi ir zinājuši par "pi" jau tūkstošiem gadu, jo tikpat ilgu laiku viņi ir strādājuši ar apļiem. Tik senas civilizācijas kā babilonieši ir spējušas aproksimēt pi līdz daudziem cipariem, piemēram, 25/8 un 256/81 daļai. Lielākā daļa vēsturnieku uzskata, ka senajiem ēģiptiešiem nebija jēdziena π un ka šī atbilstība ir nejaušība.
Pirmā rakstiskā atsauce uz pī datēta ar 1900. gadu pirms mūsu ēras. Ap 1650. gadu p.m.ē. ēģiptietis Ahmes Rindas papirusā norādīja vērtību. Babilonieši varēja noteikt, ka pi vērtība ir nedaudz lielāka par 3, vienkārši uzzīmējot lielu apli un tad uzliekot virves gabaliņu uz tā apkārtmēra un diametra, atzīmējot to attālumus un pēc tam dalot apkārtmēru ar diametru.
Zināšanas par skaitli pi nonāca atpakaļ Eiropā un ebreju rokās, kuri piešķīra šim skaitlim nozīmīgu vietu Bībeles sadaļā, ko sauc par Veco Derību. Pēc tam visizplatītākais veids, kā mēģināt atrast pi, bija uzzīmēt figūru ar daudzām malām jebkura apļa iekšpusē un izmantot figūras laukumu, lai atrastu pi. Piemēram, grieķu filozofs Arhimeds, lai atrastu pi vērtību, izmantoja daudzstūra formu ar 96 malām, bet ķīnieši 500. gadā pēc Kristus dzimšanas spēja izmantot daudzstūri ar 16 384 malām, lai atrastu pi vērtību. Grieķi, piemēram, Anaksagors no Klazomenejām, bija aizņemti arī ar citu apļa īpašību noskaidrošanu, piemēram, kā no apļiem izveidot kvadrātus un kvadrātveida skaitli pi. Kopš tā laika daudzi cilvēki ir mēģinājuši noskaidrot arvien precīzākas pi vērtības.
| Pi vēsture | ||
| Filozofs | Datums | Aproksimācija |
| ap 150. gadu pēc mūsu ēras | 3.1416 | |
| Zu Chongzhi | 430-501 CE | 3.1415929203 |
| al-Khwarizmi | ap 800. gadu pēc mūsu ēras | 3.1416 |
| al-Kashi | ap 1430. gadu | 3.14159265358979 |
| Viète | 1540-1603 | 3.141592654 |
| Roomen | 1561-1615 | 3.14159265358979323 |
| Van Ceulens | ap 1600. gadu | 3.14159265358979323846264338327950288 |
16. gadsimtā kļuva pieejami arvien labāki un labāki pi noteikšanas veidi, piemēram, sarežģītā formula, ko izstrādāja franču jurists Fransuā Vīts. Pirmo reizi grieķu simbols "π" tika izmantots 1706. gadā Viljama Džonsa sarakstītā esejā.
Matemātiķis Lamberts 1761. gadā arī pierādīja, ka skaitlis "pi" ir iracionāls, proti, to nevar pierakstīt kā daļskaitli pēc parastajiem standartiem. Cits matemātiķis vārdā Lindemans 1882. gadā arī spēja pierādīt, ka pi ir daļa no skaitļu grupas, ko dēvē par transcendentāliem skaitļiem, proti, skaitļiem, kas nevar būt polinoma vienādojuma atrisinājums.
Pi var izmantot arī daudzām citām lietām, ne tikai apļu aprēķināšanai. Pi īpašības ir ļāvušas to izmantot daudzās citās matemātikas jomās, ne tikai ģeometrijā, kas pēta figūras. Dažas no šīm jomām ir kompleksā analīze, trigonometrija un sērijas.
Pi reālajā dzīvē
Mūsdienās ir dažādi veidi, kā aprēķināt daudzus π ciparus, taču tam ir ierobežota nozīme.
Dažreiz Pi var izmantot, lai noteiktu jebkura apļa laukumu vai apkārtmēru. Lai noteiktu apļa apkārtmēru, izmantojiet formulu C (apkārtmērs) = π reiz diametrs. Lai noteiktu apļa laukumu, izmantojiet formulu π (rādiuss²). Šo formulu dažreiz raksta kā A = π r 2 {\displaystyle A=\pi r^{2}}. 
, kur r ir jebkura apļa rādiusa mainīgais lielums un A ir šī apļa laukuma mainīgais lielums.
Aprēķināt apļa apkārtmēru ar 1 mm kļūdu:
- 30 metru rādiusam ir nepieciešami 4 cipari.
- 10 cipari, ja rādiuss ir vienāds ar Zemes rādiusu.
- 15 ciparu rādiusam, kas vienāds ar attālumu no Zemes līdz Saulei.
Cilvēki parasti 14. martu atzīmē kā Pi dienu, jo 14. marts tiek rakstīts arī kā 3/14, kas simbolizē pirmos trīs skaitļus 3,14, aprēķinot pi. Pi diena tika atzīmēta 2001. gadā.
Saistītās lapas
Jautājumi un atbildes
J: Kāds ir skaitlis ً?
A: ً ir matemātiska konstante, kas ir apļa apkārtmēra attiecība pret tā diametru.
J: Ko tas rada?
A: Tas dod skaitli, un šis skaitlis vienmēr ir viens un tas pats.
J: Kā sākas šis skaitlis?
A: Skaitlis sākas kā 3,141592653589793... un turpinās bezgalīgi.
J: Kāda veida skaitļi ir šie?
A: Šos skaitļus sauc par iracionāliem skaitļiem.
J: Kāds ir apļa diametrs?
A: Apļa diametrs ir lielākā akords, ko var ievietot apļa iekšpusē, ejot caur tā centru.
J: Kas ir apļa apkārtmērs? A: Attālumu ap loku sauc par tā apkārtmēru.
Vai pi paliek nemainīgs neatkarīgi no dažādiem apļiem? A: Jā, pi ir nemainīgs neatkarīgi no dažādiem apļiem, jo to apkārtmēra un diametra attiecība vienmēr ir vienāda.
