Aplis — definīcija un formulas: rādiuss, diametrs, apkārtmērs, laukums
Uzzini, kas ir aplis — formulas rādiusam, diametram, apkārtmēram un laukumam, π vērtība un skaidri piemēri ērtai saprašanai.
Aplis ir apaļa, divdimensiju figūra — to var definēt kā to punktu kopu, kuru visi punkti atrodas vienādā attālumā no viena kopēja punkta (apļa centra). Citiem vārdiem, visi apļa malu punkti ir vienādā attālumā no centra, un šis attālums nosaka apļa izmēru.
Rādiuss
Apļa rādiuss ir līnijas segmens no apļa centra līdz apļa malai (sānu punktam). Matemātiķi apļa rādiusa garumu apzīmē ar burtu r. Rādiuss nosaka, cik "liels" aplis ir — jo lielāks r, jo lielāks aplis.
Diametrs
Apļa diametrs (no latīņu "diametrus", burtiski “cauri mērot”) ir taisna līnija, kas savieno divus pretējos apļa malas punktus un iet caur apļa centru. Matemātiķi diametru apzīmē ar burtu d. Attiecība starp diametru un rādiusu ir vienkārša: d = 2r — diametrs ir divkāršs rādiuss.
d = 2 r {\displaystyle d=2\ r}
Apkārtmērs (perimetrs)
Apļa apkārtmērs (perimetrs) ir attālums pa apļa malu — tas ir līnijas kopējais garums, kas iet ap apļa centru. Apkārtmēru apzīmē ar burtu C. Apkārtmēru var izteikt ar rādiusu vai diametru, izmantojot skaitli π:
- C = 2πr (izmantojot rādiusu)
- C = πd (izmantojot diametru)
Šīs formulas ir ekvivalentas, jo d = 2r.
Skaitlis π (pi)
Skaitlis π (rakstīts kā grieķu burts pi) ir konstante, kas ir ļoti svarīga apļiem. To definē kā apļa apkārtmēra attiecību pret tā diametru: π = C / d. Skaitlis π ir neperiodisks un bezgalīgs decimāldaļu virknē; aptuvenas vērtības ir:
- kā vienkāršs daļskaitlis: 22/7 (pieņemams aptuvens tuvinājums),
- precīzāks racionāls tuvinājums: 355/113,
- decimālskaitliskā forma: aptuveni 3,141592653589793...
Laukums
A apļa iekšpusē (apgabala laukums) izsaka ar formulu A = πr², tātad laukums ir π reizes rādiusa kvadrāts. Matemātiski to var rakstīt arī kā A = π (r × r).
Praktiski piemēri un piezīmes
- Ja rādiuss ir r = 3 cm, tad apkārtmērs C = 2π·3 ≈ 18,85 cm, un laukums A = π·3² = 9π ≈ 28,27 cm².
- Ja zināms diametrs d = 10 m, var aprēķināt rādiusu r = d/2 = 5 m, apkārtmēru C = πd ≈ 31,42 m un laukumu A = πr² ≈ 78,54 m².
- Vienības: apkārtmēram izmanto garuma vienības (m, cm, km), laukumam — kvadrāta vienības (m², cm²).
Svarīgākās īpašības īsi
- Apļa punkts, kas ir vienādā attālumā no centra, veido robežu — šo robežu parasti sauc par apļa malu (apli).
- Aplis (robeža) atšķiras no apaļas figūras ar iekšpusi (disku); diskam ir aizpildīts iekšējais laukums, aplim — tikai robeža.
- Formulas: d = 2r, C = 2πr = πd, A = πr².
Ja nepieciešami papildus piemēri vai grafiska ilustrācija formulas lietošanai, varu tos pievienot.

A aplis
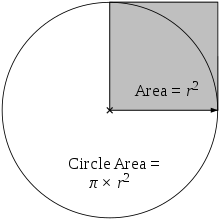
Apļa laukums ir π reizes lielāks par pelēkā kvadrāta laukumu.
π aprēķināšana
π var izmērīt, uzzīmējot lielu apli, pēc tam izmērot tā diametru (d) un apkārtmēru (C). Tas ir tāpēc, ka apļa apkārtmērs vienmēr ir π reizes lielāks par tā diametru.
π = C d {\displaystyle \pi ={\frac {C}{d}}}}
π var aprēķināt arī tikai ar matemātiskām metodēm. Lielākajai daļai metožu, ko izmanto π vērtības aprēķināšanai, ir vēlamās matemātiskās īpašības. Tomēr tās ir grūti izprast, nepārzinot trigonometriju un rēķināšanu. Tomēr dažas metodes ir diezgan vienkāršas, piemēram, šī Gregorija-Leibnica rindu forma:
π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}}-{\frac {4}{3}}+{\frac {4}{5}}}-{\frac {4}{7}}}+{\frac {4}{9}}-{\frac {4}{11}}}\cdots }
Lai gan šo rindu ir viegli uzrakstīt un aprēķināt, nav viegli saprast, kāpēc tā ir vienāda ar π. Vieglāk ir uzzīmēt iedomātu loku ar r r rādiiusu, kura centrs ir sākumpunktā. Tad jebkurš punkts (x,y), kura attālums d no sākumpunkta ir mazāks par r, aprēķināts pēc Pitagora teorēmas, atradīsies apļa iekšpusē:
d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}}
Atrodot punktu kopu apļa iekšpusē, var novērtēt apļa laukumu A. Piemēram, izmantojot veselu skaitļu koordinātas lielam r. Tā kā apļa laukums A ir π reiz rādiusa kvadrāts, π var aproksimēt, izmantojot:
π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}}
Saistītās lapas
- Sfēra
Meklēt




