Fraktālis

Fraktāls ir jebkurš raksts, kas, skatoties uz to kā uz attēlu, rada attēlu, kuru palielinot, joprojām būs tas pats attēls. To var sagriezt daļās, kas izskatās kā mazāka sākotnējā attēla versija. Vārdu fraktāls 1975. gadā Benuā Mandelbrots (Benoît Mandelbrot) izveidoja no latīņu valodas vārda fractus, kas nozīmē "salauzts" vai "lauzts". Vienkāršs piemērs ir koks, kas sazarojas mazākos zaros, un šie zari - vēl mazākos zaros utt. Fraktāli ir ne tikai skaisti, bet tiem ir arī daudz praktisku pielietojumu.

Sierpinska trīsstūris pēc 7 iterācijām.

Mandelbro kopa ir slavens fraktāla piemērs.

Piemēri

Ir daudz fraktālu veidu, kas veidoti visdažādākajos veidos. Viens no piemēriem ir Sierpinska trijstūris, kur lielā trijstūra iekšpusē ir bezgalīgs skaits mazo trijstūru. Cits piemērs ir Mandelbrota kopa, kas nosaukta Benuā Mandelbrota vārdā. Sierpinska trijstūri veido, izmantojot modeļus, bet Mandelbrota kopas pamatā ir vienādojums.

Dabā ir arī daudz dabisku fraktālu piemēru, tostarp koki, sniegpārslas, daži dārzeņi un krasta līnijas.

Koha līkne

Koha līkne ir vienkāršs fraktāla piemērs. Vispirms sāciet ar taisnas līnijas daļu, ko sauc par taisnas līnijas posmu. Sagrieziet taisni 3 vienāda izmēra gabalos. Atbrīvojieties no šo gabalu vidusdaļas un ievietojiet augšējo daļu trīsstūra, kura malas ir vienāda garuma ar izgriežamo gabalu. Tagad mums ir 4 taisnes posmi, kuru gali saskaras. Tagad mēs varam darīt to pašu, ko tikko izdarījām ar pirmo segmentu, ar katru no 4 bitiem. Tagad to pašu varam darīt atkal un atkal ar visiem galarezultātā iegūtajiem bitiem. Tagad mēs to darām bezgalīgi un skatāmies, ko esam ieguvuši.

Koha līknes garums ir bezgalība, un Koha līknes laukums ir nulle. Tas ir diezgan dīvaini. Taisnes posma (ar dimensiju 1) garums varētu būt 1, bet laukums 0. Kvadrāta ar garumu 1 un platumu 1 (ar dimensiju 2) laukums būs 1 un garums bezgalība.

Līdzības dimensija

Tātad Koča līkne šķiet lielāka nekā kaut kas ar dimensiju 1 un mazāka nekā kaut kas ar dimensiju 2. Līdzības dimensijas ideja ir dot dimensiju, kas dod labāku priekšstatu par garumu vai laukumu fraktāliem. Tātad Koča līknei vēlamies dimensiju starp 1 un 2.

Koha līkni var sagriezt četrās daļās, no kurām katra ir 1 3 {\displaystyle {\frac {1}{3}}} ${\frac {1}{3}}$ no oriģināla izmēra. Mēs saucam to gabalu skaitu, kuros var sagriezt fraktālu, par N {\displaystyle N} $N$ , un mēs saucam izmēru starpību B {\displaystyle B} $B$ . Ievietojam vienādojumā:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}} ${\frac {\log N}{-\log B}}$

Kur log {\displaystyle \log } $\log$ ir skaitļa logaritms. Šis skaitlis ir fraktāla Hausdorfa dimensija. Koha līknē tas ir log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1,2619... } ${\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619...$ , kā mēs vēlējāmies.

Koha līkne ir viena no vienkāršākajām fraktālformām, tāpēc tās dimensiju ir viegli noteikt. Tās līdzības dimensija un Hausdorfa dimensija ir vienādas. Tas neattiecas uz sarežģītākiem fraktāliem.

Koch sniegpārsliņa

Koča sniegpārsliņa (jeb Koča zvaigzne) ir tas pats, kas Koča līkne, tikai tā sākas ar vienādmalu trijstūri, nevis ar līnijas posmu.

Kā izveidot Koha līkni

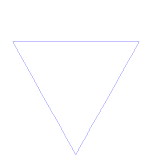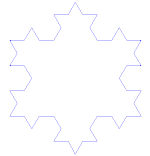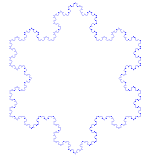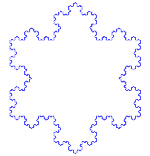
Izmanto

Fraktāliem ir daudz pielietojumu, piemēram, bioloģijā (plaušas, nieres, sirdsdarbības mainīgums utt.), zemestrīcēs, finansēs, kur tie ir saistīti ar tā saukto smago astes sadalījumu, un fizikā. Tas norāda, ka fraktāli ir jāpēta, lai saprastu, kāpēc dabā fraktāli ir tik bieži sastopami.

Daži fraktāli pastāv tikai māksliniecisku apsvērumu dēļ, bet citi ir ļoti noderīgi. Fraktāli ir ļoti efektīvas formas radio antenām, un tos izmanto datoru mikroshēmās, lai efektīvi savienotu visas sastāvdaļas. Arī krasta līnijas var uzskatīt par fraktāliem.