Dimensijas: definīcija, 3D un 4D skaidrojums matemātikā un fizikā
Uzzini, kas ir dimensijas: definīcija, 3D un 4D (laiks) skaidrojums un pielietojumi matemātikā un fizikā — vienkārši, vizuāli un precīzi.
Dimensijas ir veids, kā mēs aprakstām, redzam, mēram un izjūtam pasauli. Tās ļauj noteikt virzienus (piem., uz augšu/uz leju, no labās uz kreiso pusi), attālumus, kā arī fizikālas īpašības (karsts–auksts, smagums, garums) un abstraktākus jēdzienus matemātikā un fizikā. Viens no praktiskiem dimensijas skaidrojumiem ir saistīts ar brīvības pakāpēm — t.i., ar veidiem, kā objekts var pārvietoties noteiktā telpā. Termins "dimensija" tiek lietots dažādos kontekstos, un nav vienas universālas definīcijas, kas aptvertu visus šos kontekstus.
Vektoru telpā (vektors var tikt uzskatīts par virzienu vai virziena un garuma kombināciju) dimensija parasti tiek definēta kā vektoru bāzes elementu kardinalitāte — tas ir, minimālais skaits neatkarīgu vektoru, no kuriem var izteikt jebkuru telpas vektoru lineāri. Praktiski tas nozīmē: ja telpai nepieciešami n neatkarīgi virzieni, lai aprakstītu visus iespējamos vektorus, tad tai ir dimensija n. Piemēram, parastā trīsdimensiju telpa, ko matemātiķi sauc par Eiklīda telpu, ir trīsdimensiju, jo pietiek trīs neatkarīgiem virzieniem (garums, platums, dziļums) jeb koordinašu asīm.
Dimensijas kā pozīcijas un koordinates
Dimensijas izmanto arī pozīcijas mērīšanai. Attālumu līdz kādai pozīcijai no izvēlēta sākuma punkta parasti izsaka pa neatkarīgām dimensijām — piemēram, garuma, platuma un augstuma virzienā. Šīs koordinātas (x, y, z) nosaka punktu viennozīmīgi, ja dimensijas ir neatkarīgas. Atkarībā no problēmas var lietot arī citas koordinātu sistēmas (polāras, cilindriskas, sfēriskas), taču dimensiju skaits paliek tas pats.
0D, 1D, 2D, 3D — vienkārši piemēri
- 0 dimensijas: punkts — nav garuma, platuma vai augstuma.
- 1 dimensija: līnija vai ceļš — var pārvietoties tikai uz priekšu un atpakaļ (piem., dzelzceļš).
- 2 dimensijas: plakne — objekti var pārvietoties gar divām neatkarīgām asīm (piem., karte, zīmējums).
- 3 dimensijas: telpa — mums pazīstamā fiziskā pasaule, kurā objektam ir garums, platums un augstums (piem., kaste vai ķermenis).
Ceturtdimensija un laiks
Dažkārt tiek pievienota ceturtā (4D) dimensija — laiks, lai aprakstītu notikuma atrašanās vietu gan telpā, gan laikā. Fizikā šo pieeju izmanto, veidojot četrdimensiju laika‑telpas modeļus (piem., Minkovska laika‑telpa speciālajā relativitātē), kur katram notikumam piešķir četru koordinātu komplektu (t, x, y, z). Svarīgi atzīmēt, ka laiks fizikā darbojas citādi nekā telpas dimensijas — relatīvistiskajos rāmjos laiks un telpa ir savstarpēji saistīti, un vienlaicīguma jēdziens kļūst atkarīgs no novērotāja kustības.
Dažādas dimensiju definīcijas matemātikā
Matemātikā dimensija var tikt definēta vairākos veidos atkarībā no konteksta:
- Lineārās algebras dimensija — kā minēts, bāzes elementu skaits vektoru telpā.
- Topoloģiskā dimensija — saistīta ar atklājošām vāciņu pārklājumu īpašībām; piemēram, plaknei ir topoloģiskā dimensija 2.
- Manifolda dimensija — lokāli izskatās kā R^n; gluda virsma (piem., sfēra) ir 2‑dimensiju manifolds.
- Fraktālā vai Hausdorfa dimensija — ļauj aprakstīt "daļēji fraktālas" struktūras ar neveselu dimensiju vērtību (piem., Kokera līknes ir vairāk nekā 1, bet mazāk par 2 dimensiju).
Dimensijas fizikā un citos zinātnes laukos
Fizikā dimensiju jēdziens ietver gan telpas un laika koordinates, gan arī parametrus, kas apraksta sistēmas stāvokli. Piemēram, fāzu telpa apraksta visas iespējamās sistēmas stāvokļus un parasti ir augstākas dimensijas objekts (katram daļiņas koordinātei atbilst ātruma koordināta — kopā ļoti daudzas dimensijas). Mūsdienu teorijās, piemēram, super‑vai stīgu teorijās, tiek pieņemta papildu telpiskā dimensija pastāvēšana (kompaktificētas vai "saspiestas" nelielos mērogos), kas var būt nepieejama tiešai novērošanai.
Praktiskas piezīmes un secinājums
Dimensija ir rīks, kas palīdz strukturēt informāciju par telpiskām, laika vai vispārīgām konfigurācijas īpašībām. Atkarībā no tā, vai strādā ar vektoru telpām, manifoldiem, fraktāliem vai fizikālām sistēmām, jāizvēlas atbilstoša dimensijas definīcija. Tāpēc ir svarīgi saprast kontekstu: matemātikā dimensija bieži ir skaitlis, kas izriet no konkrētas definīcijas (bāzes lielums, topoloģiskā īpašība, Hausdorfa mērījums), savukārt fizikā dimensijas saistās arī ar mērvienībām, metriem un novērojamiem efektiem.
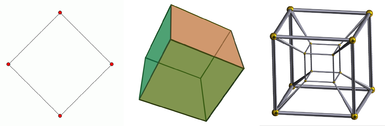
No kreisās uz labo - kvadrāts, kubs un teserakts. Kvadrāts ir divdimensiju objekts, kubs ir trīsdimensiju objekts, bet teseract ir četrdimensiju objekts. Viendimensiju objekts ir tikai līnija. Ir dota kuba projekcija, jo tas tiek skatīts uz divdimensiju ekrāna. Tas pats attiecas uz teseraktiem, kurus papildus var attēlot tikai kā projekciju pat trīsdimensiju telpā.

Pirmo četru telpisko dimensiju diagramma.
Citi izmēri
Mūsdienu zinātnē cilvēki izmanto citas dimensijas. Tādi izmēri kā temperatūra un svars var tikt izmantoti, lai parādītu kaut kā atrašanās vietu mazāk vienkāršās telpās. Zinātnieki šīs dimensijas pēta, izmantojot dimensiju analīzi.
Matemātiķi arī izmanto dimensijas. Matemātikā dimensijas ir vispārīgākas. Dimensijas matemātikā var nemērīt lietas pasaulē. Noteikumi, kā matemātikā veikt aritmētiskos aprēķinus ar dimensijām, var atšķirties no parastajiem aritmētiskajiem noteikumiem.
Izmēri un vektori
Attālumu un virzienu attēlošanai tiek izmantoti vektori. Vektorus bieži izmanto inženierzinātnēs un dabaszinātnēs, dažkārt arī matemātikā.
Vektors ir skaitļu saraksts. Katrai dimensijai ir viens skaitlis. Vektoriem ir aritmētiskie noteikumi.
Piemēram, ja Džeina vēlas uzzināt Sallijas atrašanās vietu, Sallija var sniegt Džeinai vektoru, kas parāda atrašanās vietu. Ja Džeina un Sallija atrodas pasaulē, ir trīs dimensijas. Tāpēc Sallija dod Džeinai trīs skaitļu sarakstu, lai parādītu viņas atrašanās vietu. Trīs skaitļi vektorā, ko Sally dod Džeinai, var būt šādi:
- Sally attālums uz ziemeļiem no Jane
- Sally attālums uz austrumiem no Jane
- Sally augstums virs Jane
Jautājumi un atbildes
J: Kas ir dimensija?
A: Dimensija ir veids, kā mērīt, redzēt un izjust pasauli, izmantojot tādus jēdzienus kā augšā un lejā, pa labi pa kreisi, no muguras uz priekšu, karsts un auksts, cik smags un cik garš. To var definēt arī kā brīvības pakāpes vai veidu, kā objekts var pārvietoties noteiktā telpā.
J: Kā matemātiķi definē Eiklīda telpu?
A: Matemātiķi definē Eiklīda telpu kā telpu, ko nosaka trīs dimensijas, kuras parasti sauc par garumu, platumu un dziļumu.
J: Kāds ir vektoru skaits vektoru telpā?
A: Vektoru skaits vektoru telpā ir vienāds ar tās pamatnes kopas kardinalitāti (jeb vektoru skaitu).
J: Cik dimensiju izmanto, lai izmērītu pozīciju?
A: Lai izmērītu pozīciju, izmanto trīs dimensijas (garumu, platumu un augstumu). Dažos gadījumos var izmantot ceturto (4D) dimensiju - laiku, lai parādītu notikuma atrašanās vietu laikā un telpā.
J: Ko nozīmē dim(V)?
A: Dim(V) ir V dimensija, kas ir vienāda ar tās pamatnes kopas kardinalitāti (jeb vektoru skaitu) vai vienāda ar tās taisno līniju virzienu skaitu.
Vai ir viena definīcija, kas atbilst visiem ar dimensiju saistītajiem jēdzieniem?
A: Nē, nav vienas definīcijas, kas atbilstu visiem ar dimensijām saistītiem jēdzieniem.
Meklēt