Eilera–Bernulli siju teorija: definīcija, principi un pielietojums

Eilera–Bernulli siju teorija: skaidra definīcija, pamatprincipi un praktiski pielietojumi inženierijā — vienkārši izskaidrots ar piemēriem un aprēķiniem.

Eilera–Bernulli siju teorija (pazīstama arī kā inženiera siju teorija vai klasiskā siju teorija) ir vienkāršota elastības teorija, kas paredzēta siju lieces aprēķināšanai pie nelielām pārvietojumiem un lineālas materiāla uzvedības. Tā neņem vērā bīdes deformāciju un parasti der garām (šaurām) sijām, tāpēc to bieži uzskata par īpašu Timošenko siju teorijas gadījumu. Metode radās 18. gadsimtā, to popularizēja un pielietoja inženieri 19. gadsimtā — piemēram, būvējot Eifeļa torni un Ferisa ratu — un vēlāk kļuva par pamatu daudzos inženierprojektos.

Galvenās pieņēmumi un principi

• Grieziens par neitrālo asi: šķērsgriezumi, kas sākotnēji bija plakani un taisni, saglabā savu formu un paliek perpendikulāri neitrālajai asij pēc lieces (nav šķērsgriezuma izstiepuma vai nogriešanas).
• Lineāra elastība: materiāls reaģē saskaņā ar Hooke likumu — attiecība starp spriegumu un deformāciju ir lineāra, un modulus E (Jaunga modulus) ir konstants.
• Mazas deformācijas: rotācijas un pārvietojumi ir pietiekami mazi, lai varētu izmantot linearizētas ģeometrijas attiecības.
• Negludā bīde: bīdes deformācija tiek ignorēta — visas šķērsgriezuma šķērsvirziena deformācijas tiek uzskatītas par nenozīmīgām.

Matemātiskā forma — pamata vienādojums

Standarta Eilera–Bernulli siju četrpakāpju diferenciālvienādojums viendabīgai sijas izviekumam w(x) un laukuma ārējās slodzes q(x) ir:

EI d⁴w/dx⁴ = q(x),

kur E ir Jaunga modulus, I — šķērsgriezuma vietas 2. moments (otrais inerces moments), w(x) — šķērsgriezuma pārvietojums (loka novirze) normālā virzienā, un q(x) — sadalītā šķērs slodze uz vienības garuma.

No šī vienādojuma, integrējot, iegūst attiecības starp pārvietojumu, leņķi (slīpumu), griezes momentu M(x) un šķērsgriešanas spēku V(x):

• M(x) = −EI d²w/dx²
• V(x) = dM/dx

Robežnosacījumi

Sijas risināšanai jānorāda atbilstoši robežnosacījumi. Biežāk sastopamie tipi:

• Vienkārši atbalstīta sija (simply supported): w = 0 pie atbalsta, M = 0 pie atbalsta.
• Uzkraujamā gala (cantilever): w = 0 un dw/dx = 0 pie saknes (fiksēts gals); brīvajā galā M = 0 un V = 0.
• Fiksēta–fiksēta: gan pārvietojums, gan rotācija ierobežota abos galos (w = 0, dw/dx = 0).

Pielietojumi

Eilera–Bernulli teoriju plaši izmanto praktiskā inženierijā, jo tā nodrošina ātras un precīzas aplēses daudzām parastām konstrukcijām. Tipiski pielietojumi:

• Statiska lieces analīze būvkonstrukcijās un inženierzinātnēs.
• Mašīnbūves elementu, kā sijas, assu balsti un rāmis komponentu izstrāde (mašīnbūvē).
• Civilās būves elementi — balkoni, spāres, pāļu galvenās daļas (civilā celtniecība).
• Ātrā novērtēšana slodžu ietekmei projektu sākumposmā un kontroles pārbaužu laikā.

Praktiskie ierobežojumi un kad jāizvēlas citas teorijas

• Ja bīdes deformācija nav nenozīmīga (piemēram, īsās un resnās sijās), jālieto Timošenko siju teorija, kas iekļauj bīdes efektu un šķērsgriezuma rotāciju.
• Pie ļoti lielām deformācijām (neelastiska vai geometriski nelineāra uzvedība) klasiskā teorija kļūst nepiemērota.
• Materiālu plastiskās deformācijas, laika atkarīgas īpašības (krupe, relaksācija) vai dinamiskas iedarbības gadījumos jāizmanto attiecīgas paplašinātas metodes.

Praktiski padomi

• Lietojiet Eilera–Bernulli teoriju, ja sijas garuma attiecība pret augstumu (span-to-depth ratio) ir pietiekami liela (parasti >10) un materiāls uzvedas lineāri.
• Pārliecinieties par pareizu E un I vērtību noteikšanu — I atkarīgs no šķērsgriezuma ģeometrijas, E no materiāla.
• Ja nepieciešama precizitāte pie īsām vai stipri iekrāvējamām sijām, salīdziniet rezultātus ar Timošenko risinājumu vai izmantojiet skaitliskās metodes (FEM).

Kopsavilkums

Eilera–Bernulli siju teorija ir vienkāršs, bet efektīvs modelis siju lieces aprēķinam pie nelielām deformācijām un lineālas materiāla uzvedības. Tā sniedz ātru rīku inženieriem un joprojām tiek plaši pielietota praktiskās konstrukcijās, tomēr jāievēro tās pieņēmumi un ierobežojumi — bīdes deformācijas, nelinearitātes vai īsas, resnas sijas gadījumos jāizmanto sarežģītāki modeļi.

Vēsture

Leonhards Eulers un Daniels Bernuili bija pirmie, kas 1750. gadā izveidoja šo teoriju. Tolaik zinātne un inženierzinātnes tika uztvertas citādi nekā mūsdienās. Tādas matemātiskās teorijas kā Eilesera un Bernuļa staru teorija nebija uzticamas praktiskai izmantošanai inženierzinātnēs. Tilti un ēkas līdz pat 19. gadsimta beigām tika projektētas, izmantojot tās pašas metodes. Šajā laikā Eifeļa tornis un Ferisa rats parādīja teorijas pamatotību plašākā mērogā.

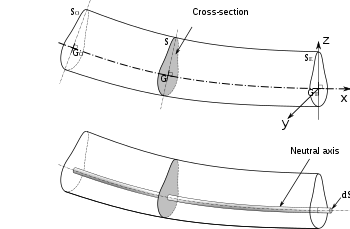
Liektas sijas šķērsgriezuma rasējums, kurā redzama neitrālā ass

Statiskās sijas vienādojums

Eilera-Bernuļa vienādojums apraksta sijas deformācijas un pieliktās slodzes sakarību, kā parādīts turpmāk:

d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{{2}}{\mathrm {d} x^{2}}}}} kreisais(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

kur w ( x ) {\displaystyle w(x)} apraksta sijas deformāciju z {\displaystyle z} virzienā kādā pozīcijā x {\displaystyle x} . q {\displaystyle q} ir sadalītā slodze, citiem vārdiem sakot, spēks uz garuma vienību (analogi spiedienam, kas ir spēks uz laukumu); tā var būt funkcija no x {\displaystyle x} , w {\displaystyle w} . vai citiem mainīgajiem.

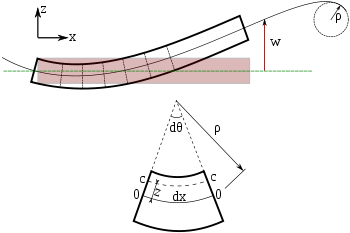
Eilesera-Bernuļa sijas liece. Katrs sijas šķērsgriezums ir 90 grādu leņķī pret neitrālo asi.

Jautājumi un atbildes

J: Kas ir Eilesera-Bernuļa staru teorija?

J: Kad pirmo reizi tika ieviesta Eilesera-Bernuļa siju teorija?

J: Vai, izstrādājot Eifeļa torni un Ferisa ratu, tika izmantota Eifeļa-Bernuļa siju teorija?

J: Kādās inženierzinātņu jomās ir izmantota Eilesera-Bernuļa siju teorija?

J: Vai Eilesera-Bernuļa siju teoriju joprojām plaši izmanto mūsdienās?

J: Kādiem sijas noviržu veidiem piemēro Eilesera-Bernuļa sijas teoriju?

J: Vai Eilesera-Bernuļa siju teorijā ir ņemta vērā bīdes deformāciju ietekme?

Meklēt pēc burta