Minkovska telpiskais laiks: definīcija un nozīme īpašajā relativitātē
Uzzini Minkovska telpisko laiku: četrdimensiju konstrukts, definīcija, metriskā signatūra (-+++), nozīme īpašajā relativitātē un salīdzinājums ar vispārējo relativitāti.
Speciālajā relativitātes teorijā Minkovska telpiskais laiks ir Hermaņa Minkovska radīts četrdimensiju daudzstūris. Tam ir četras dimensijas: trīs telpas dimensijas (x, y, z) un viena laika dimensija. Minkovska telpiskuma metriskā signatūra ir (-+++), un tas apraksta plakanu virsmu, ja tajā nav masas. Šajā rakstā pieņemts Minkovska telpas laiku saukt vienkārši par telpas laiku.
Tomēr Minkovska telpiskums ir piemērojams tikai īpašajā relativitātes teorijā. Vispārējā relativitāte izmantoja izliekta telpiskā laika jēdzienu, lai aprakstītu gravitācijas un paātrinātas kustības ietekmi.
Intervala definīcija un nozīme
Galvenais Minkovska telpiskuma rādītājs ir telpas laika intervāls starp diviem notikumiem. Ar metriku (-+++) šo intervālu parasti raksta kā:
s² = -c²t² + x² + y² + z²
Kur c ir gaismas ātrums, t — laika atšķirība, un x, y, z — telpiskās koordinātas. Intervāls s² ir invarants pret Lorenca transformācijām, t.i., to vienādi novēros visi inerciālie novērotāji. Atkarībā no s² zīmes intervālus klasificē kā:
- Laiktelpisks (timelike): s² < 0 — notikumi var būt savienojami ar hronisku (iešanas) pasaules līniju; pastāv novērotājs, kas var iziet no viena notikuma uz otru.
- Gaismas vai nulles intervāls (lightlike/null): s² = 0 — notikumi savienojami tikai ar gaismas signālu; tie atrodas uz gaismas konusa virsmas.
- Telpisks (spacelike): s² > 0 — notikumi nevar būt kauzāli saistīti; nav novērotāja, kas pārvietotos no viena notikuma uz otru ar ātrumu ≤ c.
Gaismas konuss un kauzalitāte
Minkovska telpas laiks ir vizualizējams ar gaismas konusiem, kas katrā notikumā atdala iespējamos notikumus nākotnē un pagātnē (iekšpusē konusa) no notikumiem, kuri ir "aiz konusa" un nevar ietekmēt vai tikt ietekmēti kauzāli. Šī struktūra nodrošina, ka kauzalitāte tiek saglabāta: signāli un informācija nevar pārvietoties ātrāk par gaismas ātrumu.
Četrvektori, metriķa tensora un simetrijas
Minkovska telpas laiks nodrošina dabisku vidi četrvektoriem (four-vectors) — objektiem ar četrām komponentēm, kas transformējas pēc Lorenca grupas likumiem. Metriķa tensora iekšējais produkts raksturo garumu un leņķus un parasti izsaka kā ημν = diag(-1, 1, 1, 1) (šajā signatūrā). Lorenca transformācijas saglabā metriķu formu un tādējādi arī telpas laika intervālu, kas ir īpaša relatīvitātes teorijas būtība.
Laika mēriens (īpašais laiks) un pasaules līnijas
Laiktelpiskiem pasaules līniju posmiem var definēt īpašo laiku τ, kas saistīts ar intervālu ar sakarību s² = -c²τ². Īpašais laiks ir tas, ko novērotājs pašā kustībā izmērīs ar savu pulksteni starp diviem notikumiem uz savas pasaules līnijas. Šis jēdziens skaidri attiecina laika dilšanos un garumu kontrakciju — tās nav tikai mēru artefakti, bet izriet no metrikas struktūras.
Praktiski piemēri un sekas
- Laika dilēšana: kustoties ātrauku attiecībā pret novērotāju, pulksteņi rit lēnāk salīdzinājumā ar to, kas atrodas klusi. Tas izriet no faktas, ka īstais laiks starp notikumiem uz kustīgas pasaules līnijas samazinās relativitātes efekta dēļ.
- Garuma kontrakcija: objekti, kas pārvietojas gar attiecīgajām asīm, īsumā "sarūk" novērotāja koordinātēs — tas ir otrais no Lorenca efektiem, kas izriet no intervāla invariances.
- Minkovska diagrammas: vienkāršs grafisks rīks, kur laika ass parasti tiek zīmēta vertikāli un telpas ass horizontāli; tās palīdz saprast pasaules līnijas, gaismas konusus un transformācijas starp novērotājiem.
Saites uz vispārējo relativitāti
Minkovska telpiskums apraksta plakanu, bezizliekuma telpas laiku — tas ir labs tuvinājums situācijās, kur gravitācijas lauks ir novērojami vājš vai neesošs. Vispārējā relativitāte paplašina šo ideju, aizstājot plakanu metriķi ar izliektu metriķi, kas atkarīgs no koordinātām un apraksta gravitācijas kā telpas laika ģeometrijas izlieci. Tomēr vietējās nelielās telpiskuma apgabalos jebkurā vispārēji relativistiskā risinājumā var izveidot tangenciālu Minkovska lauvas (lokālo inerciālo rāmi), kur īpašā relativitāte joprojām ir derīga tuvinājuma līmenī.
Matemātiskie un fiziskie ierobežojumi
Lai gan Minkovska telpas laiks ir ārkārtīgi noderīgs pamats, tas nav universāls: tas neaptver gravitāciju, spēcīgas ģeometrijas vai lielas masu blīvuma radītas izlieces. Arī kvantu lauka teorijas ieviešana prasa paplašinājumus un sarežģījumus, piemēram, kvantgravitācijas meklējumus, lai vienotu kvantu un ģeometrisko aprakstu.
Kopsavilkumā: Minkovska telpiskais laiks ir četrdimensiju lineārs telpas laika modelis ar metriķi (-+++), kas ir pamatā īpašajai relativitātei — tas definē invariantu intervālu, gaismas konusus, kauzalitāti un visas relatīvistiskās parādības kā laika dilēšanu un garuma kontrakciju. Vispārējā relativitāte šo plakano modeli vispārināja uz izliekto telpas laiku, lai ietvertu gravitācijas ietekmi.
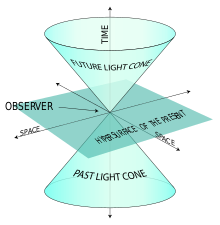
Gaismas konusa piemērs.
Definīcija(-as)
Matemātiskais
Telpisko laiku var uzskatīt par četrdimensiju koordinātu sistēmu, kurā asis ir dotas ar šādiem lielumiem.
( c t , x , y , z ) {\displaystyle (ct,x,y,z)} 
Tos var apzīmēt arī ar
( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} 
Kur x 1 {\displaystyle x_{1}}
ir c t {\displaystyle ct}
. Laiku mēra ar gaismas ātruma vienībām, reizinātām ar laika koordinātu, tāpēc, lai laika mērvienības būtu tādas pašas kā telpas mērvienības. Telpiskajā laikā ir loka garuma diferenciālis, kas izteikts kā
d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}+dz^{2}}}. 
No tā izriet, ka telpiskajam laikmetam ir metriskais tenzors, kas dots ar formulu
g u v = [ - 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0&0\0&0&1&0&0&0\0&0&0&1&0\0&0&0&0&0&1\end{bmatrix}}}} 
Kā jau minēts iepriekš, visur telpiskā telpa ir plakana; zināmā mērā to var uzskatīt par plakni.
Vienkāršs
Laiks-laiku var uzskatīt par "arēnu", kurā norisinās visi notikumi Visumā. Viss, kas nepieciešams, lai noteiktu punktu telpiskā laikā, ir noteikts laiks un tipiska telpiskā orientācija. Četras dimensijas ir grūti (praktiski neiespējami) iztēloties, taču, izmantojot tālāk aprakstīto metodi, var izveidot zināmu analoģiju.
Telpiskā laika diagrammas
Hermanis Minkovskis ieviesa noteiktu metodi koordinātu sistēmu grafēšanai Minkovska telpiskajā laikā. Kā redzams pa labi, dažādas koordinātu sistēmas nesakrīt par objekta telpisko orientāciju un/vai pozīciju laikā. Kā redzams diagrammā, ir tikai viena telpiskā ass (x ass) un viena laika ass (ct ass). Vajadzības gadījumā var ieviest papildu telpisko dimensiju (y ass); diemžēl tā ir dimensiju skaita robeža: diagrammu veidošana četrās dimensijās nav iespējama. Minkovska telpiskajā laikā grafiku veidošanas likums ir šāds:
1) Leņķis starp x-asi un x'-asi ir dots ar t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}
kur v ir objekta ātrums.
2) Gaismas ātrums caur telpiskumu vienmēr veido 45 grādu leņķi ar abām asīm.
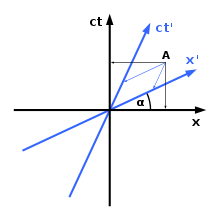
Saskaņā ar relativitātes teoriju abi novērotāji notikumu punktā A attiecina uz dažādiem laikiem.
Telpiskais laiks vispārējā relativitātes teorijā
Vispārējā relativitātes teorijā Einšteins izmantoja vienādojumu.
R u v - 1 2 g u v R = 8 π T u v {\displaystyle R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}} 
Lai nodrošinātu, ka telpiskais laiks faktiski izliekas; tā rezultātā rodas gravitācijas efekts.
Saistītās lapas
- Laiks telpā un telpā
- Speciālā relativitāte
- Vispārējā relativitāte
| Iestādes kontrole |
|
Jautājumi un atbildes
J: Kas ir Minkovska telpiskums?
A: Minkovska telplaiks ir Hermaņa Minkovska radīts četrdimensiju daudzstūris. Tajā ir trīs telpas dimensijas (x, y, z) un viena laika dimensija.
J: Kāda ir Minkovska telpiskuma metriskā signatūra?
A: Minkovska telpiskuma metriskā signatūra ir (-+++).
J: Kā Minkovska telpiskais laiks apraksta plakanu virsmu?
A: Ja nav masas, Minkovska telpiskais laiks apraksta plakanu virsmu.
J: Vai Minkovska telpaslaiks attiecas uz vispārējo relativitāti?
A.: Nē, Minkovska telpiskā laikmeta principu piemēro tikai speciālajā relativitātē. Vispārējā relativitāte izmanto izliekta telpiskuma jēdzienu, lai aprakstītu gravitācijas un paātrinātas kustības ietekmi.
J: Cik dimensiju ir Minkovsija telpiskajam laikmetam?
A:Minkovska telpiskā laika ir četras dimensijas - trīs telpas dimensijas (x, y, z) un viena laika dimensija.
J: Kas radīja Minkovsija telpiskā laika koncepciju?
A: Hermanis Minkovksi radīja Minkovska telpaslaika jēdzienu.
Meklēt