Kvantu dators
Kvantu dators ir modelis, kā uzbūvēt datoru. Ideja ir tāda, ka kvantu datori var izmantot noteiktas kvantu mehānikas parādības, piemēram, superpozīciju un savijumu, lai veiktu operācijas ar datiem. Kvantu skaitļošanas pamatprincips ir tāds, ka kvantu īpašības var izmantot, lai reprezentētu datus un veiktu ar tiem operācijas. Teorētiskais modelis ir kvantu Tjūringa mašīna, ko dēvē arī par universālo kvantu datoru.
Ideja par kvantu skaitļošanu joprojām ir ļoti jauna. Ir veikti eksperimenti. Tajos ar kubītiem (kvantu bitiem) tika veikts ļoti mazs operāciju skaits. Gan praktiskie, gan teorētiskie pētījumi turpinās ar interesi, un daudzas valstu valdības un militārās finansēšanas aģentūras atbalsta kvantu skaitļošanas pētījumus, lai attīstītu kvantu datorus gan civiliem, gan militāriem mērķiem, piemēram, kriptoanalīzei.
Mūsdienu datoros, ko dēvē par "klasiskajiem" datoriem, informācija tiek saglabāta binārajā formā; katrs bits ir vai nu ieslēgts, vai izslēgts. Kvantu skaitļošanā izmanto kubītus, kas var ne tikai būt ieslēgti vai izslēgti, bet var būt gan ieslēgti, gan izslēgti, kas ir veids, kā aprakstīt superpozīciju, līdz tiek veikts mērījums. Parastā datorā datu daļas stāvoklis ir zināms ar pārliecību, bet kvantu skaitļošanā izmanto varbūtības. Ir uzbūvēti tikai ļoti vienkārši kvantu datori, lai gan ir izgudroti arī lielāki. Kvantu skaitļošanā izmanto īpašu fizikas veidu - kvantu fiziku.
Ja izdosies uzbūvēt liela mēroga kvantu datorus, tie spēs atrisināt dažas problēmas daudz ātrāk nekā jebkurš šobrīd pastāvošais dators (piemēram, Šora algoritms). Kvantu datori atšķiras no citiem datoriem, piemēram, DNS datoriem un tradicionālajiem datoriem, kuru pamatā ir tranzistori. Dažas skaitļošanas arhitektūras, piemēram, optiskie datori, var izmantot elektromagnētisko viļņu klasisko superpozīciju. Cilvēki uzskata, ka bez kvantu mehāniskiem resursiem, piemēram, savijuma, eksponenciāla priekšrocība salīdzinājumā ar klasiskajiem datoriem nav iespējama. Kvantu datori nevar veikt funkcijas, kuras teorētiski nav iespējams aprēķināt ar klasiskajiem datoriem, citiem vārdiem sakot, tie nemaina Čērča-Tēringa tēzi. Tomēr tie spētu daudzas lietas veikt daudz ātrāk un efektīvāk.
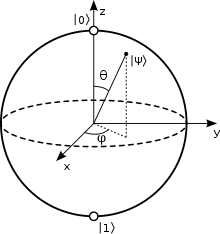
Bloha sfēra ir kubīta - kvantu datoru pamatelementa - atveidojums.
Jautājumi un atbildes
J: Kas ir kvantu dators?
A: Kvantu dators ir datora izveides modelis, kas izmanto noteiktas kvantu mehānikas idejas, piemēram, superpozīciju un savijumu, lai veiktu operācijas ar datiem.
Q: Ar ko tas atšķiras no klasiskajiem datoriem?
A.: Klasiskie datori glabā informāciju binārajā formā; katrs bits ir vai nu ieslēgts, vai izslēgts. Kvantu skaitļošanā izmanto kubītus, kas var būt gan ieslēgti, gan izslēgti, līdz tiek veikts mērījums. Parastā datorā datu daļas stāvoklis ir zināms ar pārliecību, bet kvantu skaitļošanā izmanto varbūtības.
J: Kādi ir daži iespējamie kvantu datoru lietojumi?
A: Iespējamie lietojumi ir kriptoanalīze (kodu laušana) un problēmu risināšana daudz ātrāk nekā ar jebkuru pašreizējo datoru (piemēram, Šora algoritms).
J: Vai bez kvantu datoriem ir arī citi datoru veidi?
A: Jā, ir arī citi datoru veidi, piemēram, DNS datori un tradicionālie uz tranzistoriem balstītie datori. Dažas skaitļošanas arhitektūras, piemēram, optiskie datori, var izmantot arī elektromagnētisko viļņu klasisko superpozīciju.
J: Vai Čērča un Tjūringa tēze attiecas uz kvantu skaitļošanu?
Jā, kvantu datori nevar veikt funkcijas, kuras teorētiski nav iespējams aprēķināt ar klasiskajiem datoriem; tie nemaina Čērča-Tjūringa tēzi. Tomēr tie spētu veikt daudzas lietas daudz ātrāk un efektīvāk nekā klasiskās mašīnas.
J: Vai jau ir sasniegti liela mēroga kvantu skaitļošanas rezultāti?
A: Nē, ir veikti tikai ļoti vienkārši eksperimenti, izmantojot kubītus (kvantu bitus), lai gan ir izgudrotas arī lielākas konstrukcijas. Praktiskie un teorētiskie pētījumi ar interesi turpinās, lai attīstītu liela mēroga kvantu skaitļošanas iespējas civiliem un militāriem mērķiem.
