Gausa teorēma Egregium — kas ir virsmas Gausa izliekums?
Gausa teorēma Egregium (latīņu valodā "Theorema Egregium" — nozīmē "ievērojamā teorēma") ir viens no svarīgākajiem diferenciālās ģeometrijas rezultātiem, ko pierādīja Kārlis Frīdrihs Gauss. Teorēma attiecas uz virsmu izliekumu un apgalvo, ka virsmas Gausa izliekumu var noteikt, mērot tikai leņķus, attālumus un to izmaiņu likmes uz pašas virsmas. Nav nepieciešama informācija par to, kā virsma ir iestrādāta apkārtējā trīsdimensiju Eiklīda telpā. Citiem vārdiem sakot, Gausa izliekums ir intrinseks (iekšējs) invariants: tas nemainās, ja virsmu izliek vai liec, bet neizstiepj (jeb veic izometriju).
Šī iemesla dēļ iepriekšējā rakstā minētā formula pati par sevi noved pie ievērojamās teorēmas. Ja izliekta virsma tiek attīstīta uz jebkuras citas virsmas, izliekuma mērs katrā punktā paliek nemainīgs.
Kas ir Gausa izliekums?
Gausa izliekums K katrā punktā definējas kā galveno izliekumu (k1 un k2) reizinājums: K = k1·k2. Parasti tas tiek aprēķināts, izmantojot pirmo un otro fundamentālo formu virsmas parametru izteiksmē. Ja pirmās fundamentālās formas koeficienti ir E, F, G, un otrās — e, f, g, tad
K = (eg − f²) / (EG − F²).
Kāpēc teorēma ir "ievērojama"?
- Definīcija šķiet ekstrinseka: Gausa izliekuma sākotnējā definīcija izmanto virsmas orientāciju un normālvektoru telpā (tātad izskatās atkarīga no iestrādes Eiklīda telpā).
- Tomēr rezultāts ir intrinseks: Gauss parādīja, ka K var izteikt tikai ar pirmās fundamentālās formas (tātad tikai ar attālumu, leņķu un to atvasinājumu informāciju uz virsmas) koeficientiem un to atvasinājumiem. Tāpēc K nemainās, veicot lokālas izometrijas (lieces bez stiepšanas).
Piemēri un sekas
- Plakne un cilindra virsma: abām K = 0 — tāpēc cilindru var "atvērt" līdz plaknei bez deformācijas (izometriski), kas ilustrē teorēmas nozīmi.
- Sfēra ar rādiusu R: K = 1 / R² — konstanta pozitīva izliekuma vērtība.
- Hiperboliskās virsmas (piem., pseido‑sfēra): K ir negatīvs — rāda, ka šīs virsmas nav izometriski attīstāmas uz plaknes vai uz sfēras.
- Karšu projicēšana: no Gausa teorēmas izriet, ka nevar bez izkropļojumiem pārvietot Zemes sfēras ģeogrāfiskos attālumus un laukumus uz plakni — jebkurai kartes projicēšanai būs kāds kropļojums.
Kā to pierāda — īss ieskats
Pierādījums parāda, ka Gausa izliekums izsakāms caur pirmās fundamentālās formas koeficientiem E, F, G un to atvasinājumiem, t.i., ar intrinsekiem mērījumiem uz virsmas. Teorēmas klasiskā pierādīšana izmanto divus soļus:
- izteikt izliekumu caur otro fundamentālo formu un galvenajiem izliekumiem;
- parādīt, ka šī izteiksme vienādi sakrīt ar noteiktu kombināciju no pirmai fundamentālai formas koeficientiem un to atvasinājumiem (izmantojot Kristofela simbolus un Rimana krīviņas 2D gadījumā).
Rezultātā Gausa izliekumu var interpretēt kā 2D Rimana krīviņas — tīri intrinseku ģeometrisku īpašību.
Nozīme un pielietojumi
- Gausa teorēma Egregium ir pamats mūsdienu Rimana ģeometrijai un izpratnei par to, kas ģeometriski ir intrinseks vai ekstrinseks.
- Praktiskās jomas: kartogrāfija, materiālu un elastības teorija, datorgrafika (iepakojuma/košanas problēmas), kā arī teorētā fizika (piem., lokāla telpas ģeometrija).
- Teorēma arī motivēja daudzus turpmākus pētījumus par virsmu lokālo un globālo ģeometriju, piemēram, Hilbera problēmas un Gauss–Bonnet teorēmu.
Īsi sakot, Gausa Theorema Egregium atklāja, ka izskatoties pēc ārēja jēdziena, Gausa izliekums patiesībā ir virtuozs iekšējs īpašums — tas piešķir virsmai ģeometrisku "DNS", ko nevar izmainīt tikai ar liecēm bez stiepšanas.
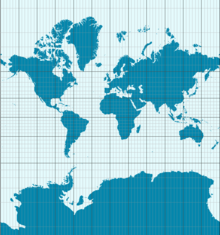
Theorema Egregium sekas ir tādas, ka Zemi nevar attēlot kartē bez izkropļojumiem. Šeit parādītā Merkatora projekcija saglabā leņķus, bet maina laukumu. Piemēram, Antarktīda ir attēlota daudz lielāka, nekā tā ir patiesībā.
Jautājumi un atbildes
J: Kas ir Gausa Theorema Egregium?
A: Gausa Egregija teorēma ir nozīmīgs diferenciālās ģeometrijas rezultāts par virsmu izliekumu, ko pierādīja Kārlis Frīdrihs Gauss.
J: Kā saskaņā ar Gausa Egreģiuma teorēmu var noteikt virsmas izliekumu?
Atbilstoši Gausa Egreģija teorēmai izliekuma izliekumu var noteikt, mērot tikai leņķus, attālumus un to likmes uz virsmas.
Vai, lai noteiktu izliekumu, ir jārunā par to, kādā veidā virsma ir iestrādāta apkārtējā trīsdimensiju Eiklīda telpā?
Atbilstoši Gausa Egregija teorēmai (Theorema Egregium), lai noteiktu izliekumu, nav jārunā par to, kādā veidā virsma ir iebūvēta apkārtējā trīsdimensiju Eiklīda telpā.
Jautājums: Vai virsmas Gausa izliekums mainās, ja virsmu izliek, to neizstiepjot?
Atbilstoši Gausa Egreģija teorēmai Gausa virsmas Gausa izliekums nemainās, ja virsmu izliek, to neizstiepjot.
J: Kurš šo teorēmu izklāstīja šādā veidā?
A: Gauss teorēmu izklāstīja šādā veidā.
J: Ar ko šī teorēma ir ievērojama?
A.: Teorēma ir "ievērojama", jo Gausa līkumainības sākuma definīcijā ir tieši izmantots virsmas novietojums telpā. Tāpēc ir diezgan pārsteidzoši, ka rezultāts nav atkarīgs no tās iestrādes, neraugoties uz visām lieces un vērpes deformācijām.
J: Kādā veidā Gauss izklāstīja teorēmu?
A.: Gauss teorēmu izklāstīja tā, ka, ja izliektu virsmu attīstītu uz jebkuras citas virsmas, izliekuma mērs katrā punktā paliktu nemainīgs.
