Elipse
Elipse ir figūra, kas izskatās kā ovāls vai saplacināts aplis.
Ģeometrijā elipse ir plaknes līkne, kas rodas, konusam krustojoties ar plakni tā, ka veidojas slēgta līkne.
Aplis ir īpašs elipses gadījums, ko iegūst, ja griešanas plakne ir perpendikulāra konusa asij. Elipse ir arī visu to plaknes punktu atrašanās vieta, kuru attālumi līdz diviem fiksētiem punktiem ir vienādi konstanti.
Aplim ir viens centrs, ko sauc par fokusu, bet elipsei ir divi fokusi.
Elipse ir vienkārši visi punkti uz grafika, kuru attālumu summa no 2 punktiem ir vienāda. Piemēram, elipsi var izveidot, ieadot kartona plāksnē divus adatas tapas un ap tiem abiem apli no auklas, pēc tam cilpā ievietojot zīmuli un velkot, cik tālu vien iespējams, nepārplīstot auklai visos virzienos. Planētu orbītas ir elipses, un vienā no tām ir saule, bet otrā - nekas.
Elipses vienādojums ir : ( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\displaystyle {\frac {(x-h)^{2}}}{a^{2}}}}+{\frac {(y-k)^{2}}}{b^{2}}}}}=1}}
kur elipses centrs ir (h,k). 2A ir garums no katra garākās, slaidākās malas
gala. 2b ir garums no abiem īsākās malas galiem. A²-B²=C², jo c ir garums starp punktiem un centru.
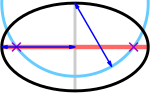
Fokusi (violeti krustiņi) ir galvenās ass (sarkanā krāsā) un apļa (zilā krāsā) ar puslielās ass (zilā krāsā) rādiusu, kura centrs ir mazās ass (pelēkā krāsā) galā, krustpunktos.
Elipse, ko iegūst kā konusa un plaknes krustpunktu.
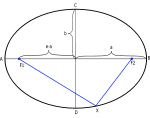
Elipse un tās īpašības.
Jautājumi un atbildes
J: Kas ir elipse?
A: Elipse ir figūra, kas izskatās kā ovāls vai saplacināts aplis. Ģeometrijā tā ir plaknes līkne, kas rodas, konusam krustojoties ar plakni tā, ka veidojas slēgta līkne.
J: Kā var izveidot elipsi?
A: Elipsi var izveidot, iespraužot kartona kārbā divus adatas tapas, tad ap šīm divām tapām savelkot auklu, cilpā iespraužot zīmuli un velkot, cik tālu vien iespējams, nepārraujot auklu visos virzienos.
J: Kas ir apļi?
A: Apļi ir elipses īpašs gadījums, kas rodas, ja griezuma plakne ir perpendikulāra konusa asij.
J: Cik fokusu ir elipsei?
A: Elipsei ir divi fokusi.
J: Kāds vienādojums apraksta elipsi?
A: Vienādojums elipsei ir (x - h)²/a² + (y - k)²/b² = 1, kur h un k apzīmē elipses centru un 2a apzīmē garumu no katra garākās malas gala, bet 2b apzīmē garumu starp abiem tās īsākās malas galiem. C ir garums starp tās fokusu un centru tā, ka A²-B²=C².
J: Kur mēs redzam eliptisku orbītu piemērus?
A: Elipsveida orbītas var redzēt planētām, kuru vienā no fokusa punktiem ir saule.
