Lineārā regresija
Lineārā regresija ir veids, kā izskaidrot atkarīgā mainīgā un viena vai vairāku paskaidrojošo mainīgo attiecību, izmantojot taisnu līniju. Tas ir īpašs regresijas analīzes gadījums.
Lineārā regresija bija pirmais regresijas analīzes veids, kas tika rūpīgi izpētīts. Tas ir tāpēc, ka modeļus, kas lineāri atkarīgi no nezināmajiem parametriem, ir vieglāk piemērot nekā modeļus, kas nav lineāri saistīti ar to parametriem. Turklāt ir vieglāk noteikt iegūto aplēšu statistiskās īpašības.
Lineārajai regresijai ir daudz praktisku pielietojumu. Lielākā daļa lietojumu ietilpst vienā no šādām divām plašām kategorijām:
- Lineāro regresiju var izmantot, lai novērojamo vērtību (datu) kopumam piemērotu prognozēšanas modeli. Tas ir noderīgi, ja mērķis ir prognozēšana, paredzēšana vai samazināšana. Ja pēc šāda modeļa izveides tiek dota papildu X vērtība, bet tai netiek pievienota y vērtība, tad piemēroto modeli var izmantot, lai prognozētu y vērtību.
- Ja ir mainīgais y un vairāki mainīgie X1, ..., Xp, kas var būt saistīti ar y, var izmantot lineāro regresijas analīzi, lai kvantitatīvi noteiktu saiknes stiprumu starp y un Xj, novērtētu, kuriem Xj vispār nav saistības ar y, un noteiktu, kuras Xj apakšgrupas satur lieku informāciju par y.
Lineārās regresijas modeļos vertikālo attālumu starp līniju un datu punktiem (piemēram, atlikumiem) cenšas padarīt pēc iespējas mazāku. To sauc par "līnijas pielāgošanu datiem". Bieži vien ar lineārās regresijas modeļiem cenšas minimizēt atlieku kvadrātu summu (mazāko kvadrātu), bet ir arī citi pielāgošanas veidi. Tie ietver "neatbilstības" minimizēšanu kādā citā normā (kā mazāko absolūto noviržu regresijā) vai mazāko kvadrātu zaudējumu funkcijas sodītas versijas minimizēšanu, kā tas ir ridge regresijā. Mazāko kvadrātu pieeju var izmantot arī tādu modeļu piemērošanai, kas nav lineāri. Kā norādīts iepriekš, termini "vismazāko kvadrātu" un "lineārs modelis" ir cieši saistīti, taču tie nav sinonīmi.
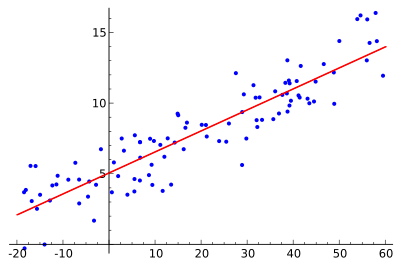
Ideja ir atrast sarkano līkni, bet zilie punkti ir faktiskie paraugi. Izmantojot lineāro regresiju, visus punktus var savienot, izmantojot vienu taisnu līniju. Šajā piemērā izmantota vienkārša lineārā regresija, kur attāluma kvadrāts starp sarkano līniju un katru parauga punktu tiek samazināts līdz minimumam.
Lietošana
Ekonomika
Lineārā regresija ir galvenais analītiskais instruments ekonomikā. Piemēram, to izmanto, lai uzminētu patēriņa izdevumus, ieguldījumus pamatlīdzekļos, ieguldījumus krājumos, valsts eksporta pirkumus, importa izdevumus, pieprasījumu pēc likvīdiem aktīviem, darbaspēka pieprasījumu un darbaspēka piedāvājumu.
Jautājumi un atbildes
J: Kas ir lineārā regresija?
A: Lineārā regresija ir veids, kā, izmantojot matemātiku, aplūkot, kā kaut kas mainās, kad mainās citas lietas. Tā izmanto atkarīgo mainīgo un vienu vai vairākus skaidrojošos mainīgos, lai izveidotu taisnu līniju, ko sauc par "regresijas līniju".
Kādas ir lineārās regresijas priekšrocības?
A: Modeļus, kas ir lineāri atkarīgi no saviem nezināmajiem parametriem, ir vieglāk piemērot nekā modeļus, kas nav lineāri saistīti ar saviem parametriem. Turklāt ir vieglāk noteikt iegūto aplēšu statistiskās īpašības.
K: Kādi ir daži lineārās regresijas praktiskie pielietojumi?
A: Lineāro regresiju var izmantot, lai piemērotu prognozēšanas modeli novērotajām vērtībām (datiem), lai veiktu prognozes, paredzējumus vai samazinājumus. To var izmantot arī, lai kvantitatīvi noteiktu attiecību stiprumu starp mainīgajiem lielumiem un identificētu datu apakškopas, kas satur lieku informāciju par citu mainīgo.
J: Kā ar lineārās regresijas modeļiem cenšas samazināt kļūdas?
A: Lineārās regresijas modeļi cenšas panākt, lai vertikālais attālums starp līniju un datu punktiem (atlikumi) būtu pēc iespējas mazāks. To dara, minimizējot vai nu atlieku kvadrātu summu (mazāko kvadrātu), vai neatbilstību kādai citai normai (mazāko absolūto noviržu), vai arī minimizējot mazāko kvadrātu zudumu funkcijas sodīto versiju (ridge regression).
Vai ir iespējams, ka lineārās regresijas modeļi nav balstīti uz mazāko kvadrātu metodi?
Jā, ir iespējams, ka lineārās regresijas modeļi nav balstīti uz mazākajiem kvadrātiem, bet tā vietā tiek izmantotas tādas metodes kā neatbilstības minimizēšana kādā citā normā (mazākā absolūtā novirze) vai mazāko kvadrātu zaudējumu funkcijas (ridge regresijas) penalizētās versijas minimizēšana.
Vai "lineārais modelis" un "vismazāko kvadrātu" ir sinonīmi?
A: Nē, tie nav sinonīmi. Lai gan tie ir cieši saistīti, "lineārais modelis" attiecas tieši uz taisnas līnijas izmantošanu, bet "vismazākie kvadrāti" attiecas tieši uz kļūdu minimizēšanu, pārliecinoties, ka starp līniju un datu punktiem ir minimāls vertikālais attālums.
