Nomogramma
Nomogramma jeb izlīdzināšanas diagramma jeb abaque ir aprēķinu grafiks. Tā ir divdimensiju diagramma, kas sniedz matemātiskas funkcijas aprēķinu.
Nomogrāfijas nozari 1884. gadā izgudroja franču inženieris Filibers Moriss d'Okāns (1862-1938). Daudzus gadus to izmantoja, lai inženieriem nodrošinātu ātrus grafiskus sarežģītu formulu aprēķinus. Nomogrammās izmanto nevis standarta Dekarta koordinātas, bet gan d'Okānā izgudroto paralēlo koordinātu sistēmu.
Nomogramma sastāv no n skalu kopuma, pa vienai katram vienādojuma mainīgajam lielumam. Zinot n-1 mainīgo lielumu vērtības, var atrast nezināmā mainīgā lieluma vērtību vai, fiksējot dažu mainīgo lielumu vērtības, var izpētīt saistību starp nefiksētajiem mainīgajiem lielumiem.
Rezultātu iegūst, noliekot lineālu pāri zināmajām vērtībām uz skalas un nolasot nezināmo vērtību no vietas, kur tas šķērso skalu attiecīgajam mainīgajam lielumam. Ar lineālu izveidoto virtuālo vai uzzīmēto līniju sauc par indeksa līniju vai izopletu.
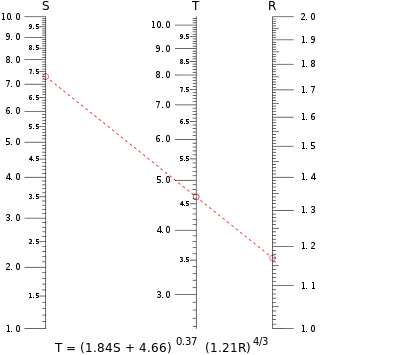
Tipiska paralēla mēroga nomogramma. Šajā piemērā ir aprēķināta T vērtība, ja vienādojumā tiek ievietota S = 7,30 un R = 1,17. Izopleja šķērso skalu T punktā nedaudz zem 4,65.
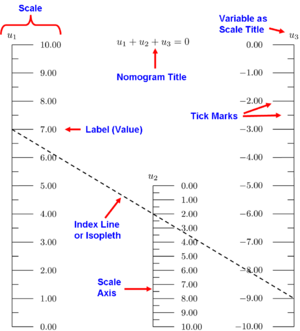
Paralēlās nomogrammas sastāvdaļas
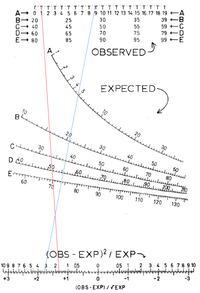
Chi-kvadrāta sadalījuma nomogramma
Izmantojiet
Nomogrammas tika plaši izmantotas aptuveni 75 gadus. Tās ļāva veikt ātrus un precīzus aprēķinus pirms kabatas kalkulatoru ēras. Rezultātus no nomogrammas iegūst ātri un droši, uzzīmējot vienu vai vairākas līnijas. Lietotājam nav jāprot risināt algebriskus vienādojumus, meklēt datus tabulās, izmantot bīdāmo lineālu vai aizvietot skaitļus vienādojumos, lai iegūtu rezultātus. Lietotājam pat nav jāzina pamatvienādojums, ko nomogramma attēlo.
Nomogrammās ir iekļautas zināšanas par domēnu. Piemēram, lai izveidotu lielākas nomogrammas, kas nodrošina lielāku precizitāti, nomogrāfs parasti iekļauj tikai tādus skalas diapazonus, kas ir pamatoti un interesanti attiecībā uz problēmu. Daudzās nomogrammās ir iekļauti arī citi noderīgi apzīmējumi, piemēram, atsauces zīmes un krāsaini reģioni. Tie visi nodrošina lietotājam noderīgus orientierus.
Tāpat kā diapozitīvs, nomogramma ir grafiska analogā skaitļošanas ierīce. Tāpat kā diapozitīvu, tā precizitāti ierobežo precizitāte, ar kādu var uzzīmēt, atveidot, apskatīt un izlīdzināt fiziskās atzīmes.Diapozitīvs ir vispārējas nozīmes kalkulators, bet nomogramma ir paredzēta konkrētu aprēķinu veikšanai. Nomogrammas joprojām var izmantot, lai pārbaudītu atbildi, kas iegūta, veicot citu, precīzāku, bet, iespējams, kļūdainu aprēķinu.
Jautājumi un atbildes
J: Kas ir nomogramma?
A: Nomogramma ir grafiks, ko izmanto aprēķiniem un kas sniedz matemātiskas funkcijas aprēķinu.
J: Kas izgudroja nomogrāfijas nozari?
A: Nomogrāfijas nozari izgudroja franču inženieris Filberts Moriss d'Okāns (Philbert Maurice d'Ocagne) 1884. gadā.
J: Kāds bija nomogrammu mērķis?
A: Nomogrammas daudzus gadus izmantoja, lai inženieriem nodrošinātu ātrus grafiskus sarežģītu formulu aprēķinus.
J: No cik skalu sastāv nomogramma?
A: Nomogramma sastāv no n skalu kopuma, pa vienai katram vienādojuma mainīgajam lielumam.
J: Kā, izmantojot nomogrammu, var atrast nezināmā mainīgā lieluma vērtību?
A: Zinot n-1 mainīgo lielumu vērtības, nezināmā mainīgā lieluma vērtību var atrast, noliekot lineālu pāri zināmajām vērtībām skalās un nolasot nezināmo vērtību no vietas, kur tā šķērso skalu šim mainīgajam lielumam.
J: Kā sauc virtuālo vai zīmēto līniju, ko izveido ar taisni?
A: Virtuālo vai zīmēto līniju, ko izveido ar lineālu, sauc par indeksa līniju vai izopletu.
J: Kāda veida koordinātu sistēmu izmanto nomogrammās?
A: Nomogrammās izmanto d'Okānā izgudroto paralēlo koordinātu sistēmu, nevis standarta Dekarta koordinātas.
