Paralaksa — astronomijas definīcija un attālumu mērīšanas metode
Uzzini, kā paralaksa ļauj astronomiem tieši mērīt attālumus līdz zvaigznēm — no Zemes orbītas trigonometrijas līdz Hipparcos un Gaia precīziem mērījumiem.
Paralaksa ir objekta izskatāmas pozīcijas izmaiņa, ko uztver, skatoties no divām dažādām vietām. To var saprast kā redzamu nobīdi pret tālāku fona objektu, kas rodas novērotāja pozīcijas maiņas dēļ.
Paralaksa astronomijā
Astronomijā gada paralakss ir viens no pamata veidiem, kā tieši noteikt attālumus līdz zvaigznēm ārpus Saules sistēmas. Paralaksa tiek definēta kā leņķis starp divām redzes līnijām uz debess objektu, kas novērotas no divām atšķirīgām pozīcijām (parasti no Zemes orbitas pretējām pusēm sešu mēnešu intervālā). Tuvākiem objektiem šis leņķis ir lielāks nekā attālākiem, tāpēc paralaksu var izmantot trigonometrijai balstītu attāluma noteikšanai.
Mērīšana un vienības
Paralaksa tiek mērīta kā ļoti mazs leņķis — astronomijā to bieži izsaka ar leņķa vienībām arkssekundēs (arcsec) vai arksiļsekundēs (milliarcsecond, mas) un pat mikroarcsekundēs. Ja paralakses leņķis ir p (arcssekundēs), tad attālumu d (parsekos) nosaka ar vienkāršu formulu d = 1 / p. Vienu parseku definē kā attālumu, no kura Zemes orbīta puslīdzība (1 astronomiskā vienība) subtendē leņķi vienu arkssekundi; 1 parseks ≈ 3,26 gaismas gadi.
Praktiski trigonometrijas aprēķinos novērojumi no divām stāvokļiem veido tuvu trijstūri: bāzes līnija (piemēram, 2 AU, ja izmanto abas Zemes orbitas puses) un novērojumu leņķi ir zināmi, līdz ar to var aprēķināt attālumu. Tāds apraksts ir pamats, kā minēts: no trīsstūra ar trigonometrijas palīdzību aprēķina attālumu un izsaka parsekos.
Praktiskie aspekti, ierobežojumi un risinājumi
Šī metode darbojas ļoti labi priekš relatīvi tuviem objektiem, bet neizdodas, ja objekti atrodas tik tālu, ka Zemes orbīta vai cits pieejamais bāzes garums ir pārāk mazs, lai radītu mērāmu paralakses leņķi attiecībā pret instrumentu precizitāti. Agrāk zemes novērojumu un instrumentu ierobežojumu dēļ ticami paralakses mērījumi bija iespējami tikai līdz salīdzinoši nelielam attālumu aplim. Telpā veikti mērījumi ir mainījuši šo robežu un būtiski paplašinājuši teritoriju, kurā trigonometrijas paralakss sniedz precīzas attāluma vērtības.
Historiski paralakses princips tika izmantots arī, lai noteiktu attālumus līdz tuvākajiem objektiem: Mēness un Saule attālumus var mērīt, izmantojot atšķirīgas bāzes (piemēram, Zemes rādiusu vai novērojumu laika nobīdi). Piemēram, Saules paraksa bija būtiska, lai noteiktu astronomisko vienību (AU) un tālākos mērogus Saules sistēmā; vēsturiskie novērojumi, tostarp Venera pārejas, tika izmantoti, lai aprēķinātu AU.
Lai pārvarētu leņķa mērījumu ierobežojumus attālākām zvaigznēm, astronomi izmanto kosmiskās astrometrijas misijas un tehnoloģijas, kas nodrošina lielāku precizitāti. No 1989. līdz 1993. gadam Hipparcos satelīts veica mērījumus vairāk nekā 100 000 tuvāko zvaigžņu, sniedzot precizitāti aptuveni milisekunžu (mas) līmenī. Mūsdienās Gaia (kosmiskais aparāts) un tai līdzīgas misijas spēj noteikt paralakses ar daudz augstāku precizitāti (mikroarcsekunžu līmenī), ļaujot precīzi izmērīt attālumus miljoniem līdz miljardiem zvaigžņu un paplašināt paralakses metodei pieejamo telpas apjomu.
Paralaksa kosmisko attālumu skalā
Paralakss nodrošina pamatu kosmisko attālumu kāpnēm, kas ļauj kalibrēt tālāku nestandarta metožu atkarību no tiešajiem attālumiem. Piemēram, paraklasa mērījumi zvaigznēm, kas ir arī Cepīda mainīgās zvaigznes vai citu standarta sveču tipiem, tiek izmantoti, lai noteiktu šo objekta absolūto spožumu. Salīdzinot ar redzamo spožumu, var aprēķināt vēl lielākus attālumus (piemēram, uz citām galaktikām). Tā paralakss kļūst par pamatu tālākām metēm kā Cepheīdu zvaigžņu un tipa Ia supernovu kalibrēšanai.
Moderna tehnoloģija un precizitāte
Mūsdienu astrometrija izmanto dažādas metodes un instrumentus: no zemes bāzes teleskopiem, interferometrijas un Very Long Baseline Interferometry (VLBI) līdz kosmiskiem observatorijām, kas novērš atmosfēras traucējumus. Katra metode dod savu nosacījumu attiecībā uz to, cik mazu paralakses leņķi iespējams uztvert, bet kopumā kosmiskie projektī ir vairākkārtīgi uzlabojuši precizitāti salīdzinājumā ar agrāk pieejamo.
Bioloģiskā paralaksa — dziļuma uztvere
Daudziem dzīvniekiem, tostarp cilvēkiem, ir divas acis, kas nodrošina dziļuma uztveri; to sauc par stereopsi. Tā kā abas acis atrodas dažādās galvas vietās, tās redz nedaudz atšķirīgas projekcijas no tās pašas skatuves; smadzenes salīdzina šīs atšķirības un veido automātisku attāluma uztveri. Rezultātā mēs parasti uztveram pasauli kā trīsdimensionālu ainavu (trīsdimensiju).
Kopumā paralaksa ir fundamentāls un intuitīvs princips — gan astronomijā, gan bioloģiskajā uztverē — kas ļauj noteikt attālumus, pamatojoties uz novērotāja pozīcijas maiņu un leņķisko novirzi pret fona objektiem.
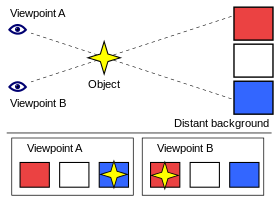
Objekta paralakses piemērs pret attālu fonu, ko izraisa atrašanās vietas maiņa. Skatoties no "skatpunkta A", objekts šķiet atrodamies zilā kvadrāta priekšā. Kad skatpunkts tiek mainīts uz "skatpunktu B", objekts šķiet pārvietots sarkanā kvadrāta priekšā.
Jautājumi un atbildes
J: Kas ir paralakse?
A: Paralaksa ir objekta stāvokļa izmaiņas, ko uztver, skatoties no divām dažādām vietām. To mēra pēc leņķa starp divām novērošanas līnijām, un to var izmantot attālumu noteikšanai.
J: Kā paralaksi izmanto astronomijā?
A: Astronomijā gada paralakss ir vienīgais tiešais veids, kā izmērīt attālumu līdz zvaigznēm ārpus Saules sistēmas. Astronomi izmanto paralakses principu, lai mērītu attālumus līdz debess objektiem, tostarp līdz Mēnesim, Saulei un zvaigznēm ārpus Saules sistēmas.
J: Kā aprēķina attālumu, izmantojot paralakses metodi?
A: Astronomiskie stāvokļa mērījumi tiek veikti dažādos gada laikos. Tā kā Zemes orbīta ir precīzi zināma, var aprēķināt attālumu no 1. pozīcijas līdz 2. pozīcijai. Var precīzi izmērīt leņķi no horizonta līdz objektam, tādējādi iegūstot trīsstūri, kura bāzes līnija un leņķi ir precīzi zināmi. No šī trijstūra ar trigonometrijas palīdzību var aprēķināt attālumus, kas izteikti parsekos.
J: Vai ir kādi ierobežojumi, izmantojot paralakses metodi attālu objektu mērīšanai?
A: Jā, tas neizdodas, ja objekti ir tik tāli, ka Zemes orbīta ir pārāk maza, lai paralakses leņķis būtu pietiekami liels precīziem mērījumiem - aptuveni 100 vai vairāk gaismas gadu attālumā. Ir izgudrotas citas metodes, bet neviena no tām nav tik precīza kā paralakss salīdzinoši tuviem objektiem.
J: Kādu satelītu izmantoja tuvāko zvaigžņu mērījumiem 1989.-1993. gadā?
A: Šajā laika posmā tika izmantots Hipparcos satelīts, kas veica mērījumus vairāk nekā 100 000 tuvāko zvaigžņu.
J: Kāds kosmiskais aparāts veiks līdzīgus mērījumus kā Hipparcos? A: Gaia (kosmiskais aparāts) veiks līdzīgus mērījumus aptuveni miljardam zvaigžņu.
Meklēt