Varbūtību telpa
Varbūtību telpa ir matemātisks modelis, ko izmanto zinātnisko eksperimentu aprakstīšanai Varbūtību telpa sastāv no trim daļām:
- Paraugu telpa, kurā uzskaitīti visi iespējamie rezultāti
- Notikumu kopums. Katrs notikums ir saistīts ar nulli vai vairākiem iznākumiem
- Funkcija, kas katram notikumam piešķir varbūtību.
Iznākums ir vienreizējas modeļa izpildes rezultāts. Tā kā atsevišķi rezultāti var būt maz praktiski izmantojami, rezultātu grupu raksturošanai tiek izmantoti sarežģītāki notikumi. Visu šādu notikumu kopums ir σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}}. 
. Visbeidzot, ir jāprecizē katra notikuma iestāšanās varbūtība. To veic, izmantojot varbūtības mērvienības funkciju P.
Kad varbūtību telpa ir izveidota, tiek pieņemts, ka "daba" veic savu gājienu un izvēlas vienu iznākumu ω no izlases telpas Ω. Par visiem notikumiem F {\displaystyle \scriptstyle {\mathcal {F}}}}, kas satur izvēlēto iznākumu ω (atcerieties, ka katrs notikums ir Ω apakškopa), tiek uzskatīti par "notikušiem". Dabā veiktā atlase notiek tā, ka, ja eksperiments tiktu atkārtots bezgalīgi daudz reižu, katra notikuma relatīvais iestāšanās biežums sakristu ar funkcijas P noteiktajām varbūtībām.
Ievērojamais padomju matemātiķis Andrejs Kolmogorovs pagājušā gadsimta 30. gados kopā ar citām varbūtības aksiomām ieviesa varbūtības telpas jēdzienu.
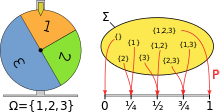
Laimes rata modelēšana, izmantojot varbūtību telpu
Jautājumi un atbildes
J: Kas ir varbūtības telpa?
A: Varbūtību telpa ir matemātisks modelis, ko izmanto, lai aprakstītu zinātniskus eksperimentus. Tā sastāv no trim daļām: izlases telpas, kurā uzskaitīti visi iespējamie iznākumi, notikumu kopuma, kas asociē nulles vai vairākus iznākumus, un funkcijas, kas katram notikumam piešķir varbūtību.
J: No kā sastāv izlases telpa?
A: Izlases telpa sastāv no visiem iespējamiem iznākumiem, ko bieži raksta kā Ω {\displaystyle \Omega }. un iznākums kā ω {\displaystyle \Omega }. .
J: Kas ir iznākums?
A: Iznākums ir modeļa vienas izpildes rezultāts.
J: Kādam nolūkam varbūtību telpās izmanto notikumus?
A: Notikumus izmanto, lai raksturotu iznākumu grupas, jo atsevišķi iznākumi var būt maz praktiski izmantojami. Visu šādu notikumu kopumu sauc par σ-algebru, dažreiz to raksta kā F {\displaystyle {\mathcal {F}}} .
J: Kā katram notikumam tiek piešķirta varbūtība?
A: Katram notikumam piešķir varbūtības, izmantojot varbūtības mērvienības funkciju P.
J: Kas ieviesa jēdzienu "varbūtību telpas"? A: Ievērojamais padomju matemātiķis Andrejs Kolmogorovs pagājušā gadsimta trīsdesmitajos gados kopā ar citām varbūtības aksiomām ieviesa varbūtību telpas jēdzienu.
