Labās rokas noteikums — vektoru krustprodukta virziena noteikšana
Labās puses noteikums ir vektoru matemātikas konvencija. Tas palīdz atcerēties virzienu, kad vektori tiek savstarpēji reizināti.
1. Sāciet, aizverot labo roku un izstiepjot rādītājpirkstu.
2. Ielieciet īkšķi taisni uz augšu, it kā dotu zīmi ierocim.
3. Ja vēršat "pistoli" taisni uz priekšu, izstiepiet vidējo pirkstu tā, lai tas būtu vērsts pa kreisi un visi pirksti atrastos taisnā leņķī viens pret otru.
Ja jums ir divi vektori, kurus vēlaties reizināt krustu šķērsu, jūs varat noteikt iznākošā vektora virzienu, rādot īkšķi pirmā vektora virzienā un rādītāju otrā vektora virzienā. Vidējais pirksts norādīs krusteniskā reizinājuma virzienu.
Atcerieties, ka, mainot secību, kādā vektori tiek savstarpēji reizināti, rezultāts būs pretējā virzienā. Tāpēc ir svarīgi pārliecināties, ka jūs ejat secībā — īkšķis → × rādītājs → = vidējais pirksts. 
Kas jāzina par krustproduktu
Krustprodukta virziens vienmēr ir perpendikulārs abiem sākotnējiem vektoriem — tas ir, vektors a × b ir taisns uz leju vai uz augšu no plaknes, ko veido a un b, atkarībā no to secības.
Magnitūda (lielums) ir |a × b| = |a| |b| sin θ, kur θ ir leņķis starp vektoriem a un b. Tātad krustprodukts ir nulles vektors, ja vektori ir paralēli (θ = 0° vai 180°).
Īpašības, ko jāatceras:
- Antikomutativitāte: a × b = −(b × a). Tas atspoguļo to, ka mainot vektoru secību, virziens apgriežas.
- Linearitāte: (c a) × b = c (a × b) un a × (b + c) = a × b + a × c.
- Nulles gadījums: a × a = 0, jo sin 0 = 0.
Praktiski piemēri un lietojumi
Standarta bāzes vektori trīs dimensijās: i × j = k, j × k = i, k × i = j. Mainot secību, piemēram, j × i = −k.
Fizikas piemēri:
- Grieze (moments): moments τ = r × F; virziens norāda rotācijas asi, kas definēta ar labās rokas noteikumu.
- Magnētiskā spēka formula: F = q v × B (lādētai daļiņai q). Ja q ir negatīvs (piemēram, elektrons), tad virziens būs pretējs parasto labo roku noteikuma rezultātam.
Padomi un brīdinājumi
Secība ir izšķiroša. Vienmēr pārliecinieties, kurš vektors ir pirmais un kurš otrais — kļūda secībā dod pretēju rezultātu.
Labās rokas sistēma pret kreisās rokas sistēmu. Labās rokas noteikums ir saistīts ar labās rokas koordinātu sistēmu, ko lieto fizikas un inženierijas standartos. Dažos kontekstos (piemēram, konkrētās orientācijās vai dažās elektriskajās shēmās) var izmantot kreisās rokas interpretāciju, taču tad tas nozīmē, ka orientācija ir pretēja.
Ja nepieciešams, praktizējiet ar faktiskām rokām un vienkāršiem vektoriem, lai iegūtu intuitīvu izpratni — tas parasti ir ātrākais veids, kā droši noteikt krusteniskā reizinājuma virzienu.
Labās rokas likums kustībai, kas radīta ar skrūvju vītnēm
Kreisās puses orientācija ir attēlota pa kreisi, bet labās puses - pa labi.
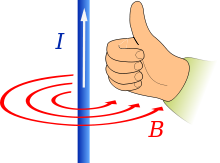
Lauka virziena (B) prognozēšana, ja strāva I plūst īkšķa virzienā
Variācijas
Pastāv vēl viens noteikums, ko sauc par labās rokas satvēriena noteikumu (vai korķa skrūves noteikumu), ko izmanto attiecībā uz magnētiskajiem laukiem un rotējošām lietām.
1. Sāciet, noliekot labo roku plakaniski un novietojiet īkšķi taisni uz āru tā, lai tas būtu taisnā leņķī pret pārējiem pirkstiem.
2. Tagad savelciet pirkstus dūrienā un īkšķi turiet ārā (kā īkšķi uz augšu).
3. Pielāgojiet pirkstu izliekumu tam, kā kaut kas kustas. Virziens, uz kuru norāda īkšķis, ir vektora virziens, ko mēs izmantojam, lai par to runātu.
To var izdarīt arī otrādi, sākot ar īkšķi vektora virzienā un vērojot, kā savelkas pirksti, lai redzētu rotācijas virzienu. Ja īkšķi pavēršat strāvas virzienā vadā, tad magnētiskais lauks, kas rodas ap to, ir jūsu pirkstu izliekšanās virzienā.
Jautājumi un atbildes
J: Kas ir labās rokas likums?
A: Labās puses noteikums ir vektoru matemātikas konvencija, kas palīdz atcerēties virzienu, kad vektori tiek savstarpēji reizināti.
J: Kā izmantot labās rokas noteikumu, lai noskaidrotu krusteniskā reizinājuma virzienu?
A: Lai noskaidrotu krusteniskā reizinājuma virzienu, aizveriet labo roku un pavelciet rādītājpirkstu. Paliec īkšķi taisni uz augšu, it kā tu taisītu zīmi ierocim. Virziet savu "pistoli" taisni uz priekšu, tad izstiepiet vidējo pirkstu tā, lai tas būtu vērsts pa kreisi un visi pirksti būtu viens pret otru taisnā leņķī. Rādi īkšķi pirmā vektora virzienā un rādītāju otrā vektora virzienā. Vidējais pirksts rādīs krusteniskā reizinājuma virzienā.
Jautājums: Kas notiek, ja mainās secība, kad vektori tiek savstarpēji reizināti?
A: Ja mainās secība, kad vektori tiek reizināti krusteniski, rezultāts būs pretējos virzienos. Tāpēc ir svarīgi pārliecināties, ka jūs ejat tādā secībā kā īkšķis x rādītājs = vidējais .
J: Ko nozīmē šis vienādojums? {\displaystyle {\vec {palielāks}}}\times {\vec {rādītājs}}} = {{\vec {vidējais}}} .
A: Šis vienādojums nozīmē, ka, ja divi vektori tiek savstarpēji reizināti (īkšķis x rādītājs), tad rezultātā tiek iegūts trešais vektors (vidus).
