Furjē sērija
Žozefs Furjē teica, ka ir iespējams izmantot sinusoidālos viļņus, lai aproksimētu citu funkciju. Tā ir virkne matemātiskā nozīmē. Šo teoriju var vispārināt uz Furjē transformāciju. Šo funkciju matemātisko analīzi sauc par Furjē analīzi.
Jau 18. gadsimtā tādi matemātiķi kā Ēlers, Lagranžs un Bernuili izmantoja sinusoīdas, lai aproksimētu un modelētu citas funkcijas. Kad Furjē 1822. gadā publicēja darbu par siltumu, viņš teica, ka šādas aproksimācijas pastāv jebkurai šādai funkcijai (kas ir nepārtraukta intervālā). Sākumā cilvēki viņam neticēja, un pagāja gandrīz desmit gadi, līdz parādījās pierādījums (daļai problēmas).
Mūsdienās Furjē sērijas tiek plaši izmantotas ciparu signālu apstrādē.
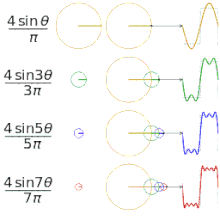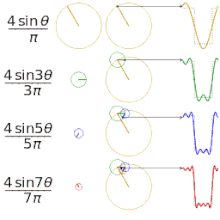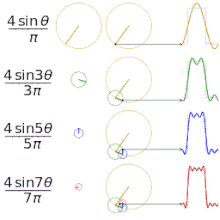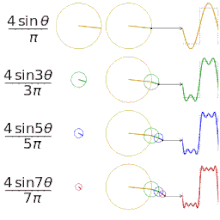
Dažādu "kvadrātveida" funkciju aproksimēšana, izmantojot Furjē virknes
Jautājumi un atbildes
J: Kas bija Žozefs Furjē?
A: Žozefs Furjē bija franču matemātiķis, kurš ierosināja, ka sinusoidālos viļņus var izmantot, lai aproksimētu citu funkciju.
J: Kas ir Furjē rinda?
A: Furjē rinda ir rinda, kurā izmanto sinusoidālos viļņus, lai aproksimētu citu funkciju.
J: Kas ir Furjē transformācija?
A: Furjē transformācija ir teorijas vispārinājums, kurā izmanto sinusoidālos viļņus, lai aproksimētu citu funkciju.
J: Kas ir Furjē analīze?
A: Furjē analīze ir funkciju matemātiska analīze, kas izmanto sinusoidālos viļņus, lai aproksimētu citu funkciju.
J: Kas 18. gadsimtā izmantoja sinusoīdas citu funkciju aproksimācijai un modelēšanai?
A: Tādi matemātiķi kā Eulers, Lagrange un Bernoulli 18. gadsimtā izmantoja sinusoīdes, lai aproksimētu un modelētu citas funkcijas.
J: Ko ierosināja Furjē savā darbā par siltumu 1822. gadā?
A: Savā 1822. gada darbā par siltumu Furjē ierosināja, ka šādas aproksimācijas, izmantojot sinusoīdas, pastāv jebkurai nepārtrauktai funkcijai dotajā intervālā.
J: Kāds ir Furjē rindu pielietojums ciparu signālu apstrādē?
A: Furjē virknes daudz izmanto ciparu signālu apstrādē, lai aproksimētu un analizētu signālus.
