Kas ir Furjē transformācija — definīcija, piemēri un pielietojumi
Uzzini Furjē transformācijas definīciju, skaidrus piemērus un praktiskus pielietojumus signālu apstrādē, fizikā, mašīnmācībā un radioloģijā.
Furjē transformācija ir matemātiska funkcija, ko izmanto, lai noteiktu signāla vai viļņa bāzes frekvences. Piemēram, ja tiek atskaņots akords, šī akorda skaņas vilni var ievadīt Furjē transformācijā, lai atrastu atsevišķās notis, no kurām akords sastāv. Furjē transformācijas izvadi dažkārt sauc par frekvenču spektru vai sadalījumu, jo tā attēlo ievades signāla frekvenču saturu. Šo transformāciju plaši izmanto kriptogrāfijā, okeanogrāfijā, mašīnmācībā, radioloģijā, kvantu fizikā, kā arī skaņas dizainā un vizualizācijā.
Matemātiskā definīcija
Reālā vai kompleksa vērtību funkcijas f ( x ) {\displaystyle f(x)}
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx}
Šeit α {\displaystyle \alpha } 



Inversā Furjē transformācija
Lai atjaunotu sākotnējo funkciju no tās frekvenču spektra, izmanto inverso transformāciju:
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha }d\alpha }
Atcerieties, ka eksistē vairākas normalizācijas konvencijas (piemēram, izmantojot 2π priekšā vai 1/√(2π) faktoros). Nozīmīgākais ir tas, ka Furjē transformācija ir invertējama (pie attiecīgiem nosacījumiem), t.i., no spektra var atgūt laika domēna signālu.
Skaidrojums un vizuāla interpretācija
Furjē transformācija rāda, kā signāls ir uzbūvēts no sinusoidālām komponentēm: katrai frekvencei atbilst amplitūda (un fāze), kas norāda, cik spēcīgi šī frekvence piedalās signālā. Piemēram, aplūkojot skaņas vilni, kurā ir trīs dažādas notis, Furjē spektrā par katru no šīm notīm būs atsevišķs maksimums (pīķis) — tas attēlo frekvences klātbūtni un to intensitāti.
Daudzi signāli īsti sastāv no kosinusiem un sinusiem ar dažādām amplitūdām un frekvencēm. Furjē transformācija parāda šo komponentu amplitūdas un fāzes pret to attiecīgajām frekvencēm.
Prasības, kad transformācija eksistē
Lai kontinuāla Furjē transformācija eksistētu klasiskā formā, funkcijai parasti jābūt integrējamai (piemēram, f ∈ L1) vai kvadrātintegrējamai (f ∈ L2) atbilstoši teorētiskajam kontekstam. Ja šie nosacījumi netiek izpildīti, nepieciešams izmantot vispārīgākas pieejas (piemēram, sadalījumu teoriju — Diraka delta u.c.).
Diskrētā Furjē transformācija un ātrā Furjē transformācija
Reālās pasaules mērījumi parasti ir diskrēti un ierobežoti laika intervālā. Tādēļ izmanto diskrēto Furjē transformāciju (DFT), kas strādā ar virknēm un ir skaitliski aprēķināma. Lai šo DFT aprēķinātu efektīvi, izmanto algoritmu ātrā Furjē transformācija (FFT), kas samazina aprēķinu sarežģītību no O(N²) uz O(N log N). Tāpēc FFT ir plaši izmantots signālu apstrādē un inženierijā.
Būtiskas īpašības
- Linearitāte: transformācija ir lineāra — Furjē no summas ir summu Furjē.
- Pārbīde (shift): laika pārbīde atbilst fāzes modulācijai frekvenču domēnā.
- Skalēšana: laika mērogošana ietekmē frekvenču izvietojumu pretēji (sākotnējā funkcijas paplašināšana sašaurina spektru).
- Parsevala (Plancherel) teorēma: enerģija laika domēnā saglabājas frekvenču domēnā (integrāla/no kvadrāta summa).
- Konvolūcijas teorēma: konvolūcija laika domēnā atbilst reizinājumam frekvenču domēnā, un otrādi — šī īpašība ir pamats filtrēšanai un sistēmu analīzei.
Piemēri un ilustrācijas
Piemēram, signālam, kas svārstās ar 3 Hz, tā Furjē transformācija koncentrēs enerģiju pie 3 Hz. Ja signāls satur vairāk komponentu (piemēram, 3 Hz un 5 Hz), spektrā būs pīķi pie abām frekvencēm.
· 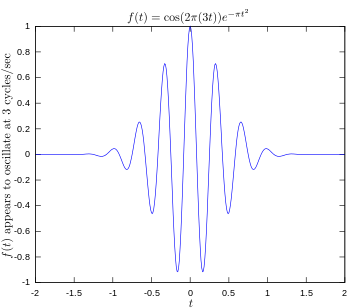
Sākotnējā funkcija, kas attēlo signālu, kurš svārstās ar frekvenci 3 herci.
· 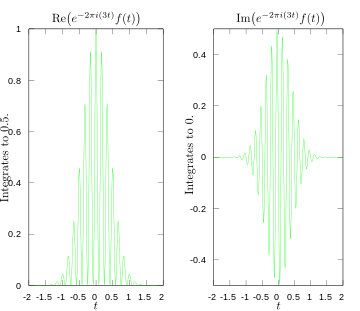
Integranta reālā un iedomātā daļa Furjē transformācijai pie 3 herciem.
· 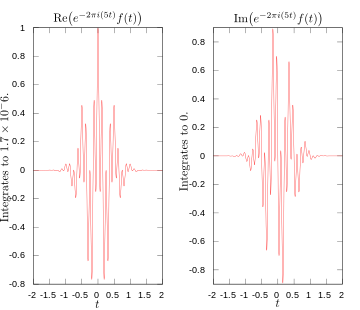
Integranta reālā un iedomātā daļa Furjē transformācijai pie 5 herciem — atšķirīga fāze un amplitūda, salīdzinot ar 3 Hz gadījumu.
· 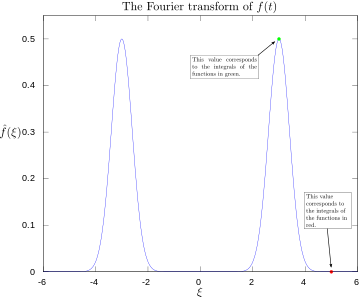
Furjē transformācijas spektrs ar marķējumiem 3 un 5 herci — redzami pīķi atbilstošajām frekvencēm.
Pielietojumi praksē
- Audio apstrāde: notju atpazīšana, trokšņu filtrēšana, skaņas efekti un kompresija.
- Attēlu apstrāde: frekvenču filtrēšana, malas pastiprināšana, attēlu kompresija (piem., JPEG izmanto kosinusu transformācijas variantu).
- Telekomunikācijas: spektrālā analīze, modulācija un signālu demodulācija.
- Fizika un inženierija: viļņu analīze, kvantu mehānikā pārejas starp laika un frekvenču attēlojumu.
- Datu analīze un mašīnmācība: laika sēriju analīze, iezīmju iegūšana frekvenču domēnā.
Kopsavilkums
Furjē transformācija ir pamattīkls signālu analīzē: tā pārveido laika (vai telpas) atkarīgu funkciju uz frekvenču domēnu, atklājot, kādas sinusoīdu komponentes to veido. Teorētiski un praktiski tā ir neaizstājama daudzu inženierijas, fizikas un datu apstrādes jomu rīkkopa. Lai strādātu ar diskretiem datiem un lieliem signāliem, izmanto DFT un ātrās FFT metodes, kas padara Furjē analīzi skaitliski efektīvu.
Jautājumi un atbildes
J: Kas ir Furjē transformācija?
A: Furjē transformācija ir matemātiska funkcija, ko var izmantot, lai atrastu viļņa bāzes frekvences. Ar šo metodi iegūst kompleksu vilni un atrod to veidojošās frekvences, kas ļauj noteikt notis, no kurām sastāv akords.
J: Kādi ir daži Furjē transformācijas izmantošanas veidi?
A: Furjē transformācija tiek plaši izmantota kriptogrāfijā, okeanogrāfijā, mašīnmācībā, radioloģijā, kvantu fizikā, kā arī skaņas dizainā un vizualizācijā.
J: Kā aprēķina Furjē transformāciju?
A: Funkcijas f(x) Furjē transformāciju nosaka F(ב) = ∫-∞+∞f(x)e-2נiבxdx, kur ב ir frekvence. Tas atgriež vērtību, kas parāda, cik izplatīta frekvence ב ir sākotnējā signālā. Atkārtotā Furjē transformācija ir f(x) = ∫-∞+∞F(ב)e+2נixבdב.
J: Kā izskatās Furjē transformācijas izvads?
A: Furjē transformācijas rezultātu var saukt par frekvenču spektru vai sadalījumu, jo tas attēlo ievades iespējamo frekvenču sadalījumu.
J: Kā datori aprēķina ātro Furjē transformāciju?
A: Datori izmanto algoritmu, ko sauc par ātro Furjē transformāciju (FFT), lai ātri aprēķinātu jebkuru, izņemot vienkāršāko signālu transformācijas.
J: Ko mums nerāda signālu aplūkošana attiecībā pret laiku?
A: Skatoties uz signāliem attiecībā pret laiku, nav skaidrs, kādas notis tajos ir; daudziem signāliem ir lielāka jēga, ja to frekvences tiek atdalītas un analizētas atsevišķi.
Meklēt

