Biežuma sadalījums
Biežumu sadalījums statistikā ir saraksts ar mainīgā lieluma vērtībām izlasē. Parasti tas ir saraksts, kas sakārtots pēc daudzuma. Tas parāda, cik reizes parādās katra vērtība. Piemēram, ja 100 cilvēki novērtē savu piekrišanu kādam apgalvojumam piecu punktu Likerta skalā, kur 1 nozīmē stingru piekrišanu un 5 - stingru nepiekrišanu, viņu atbilžu biežuma sadalījums varētu izskatīties šādi:
Šai vienkāršai tabulai ir divi trūkumi. Ja mainīgais lielums var iegūt nepārtrauktas vērtības, nevis diskrētas vērtības, vai ja iespējamo vērtību skaits ir pārāk liels, tabulas izveide ir sarežģīta, ja tā nav neiespējama. Šādos gadījumos izmanto nedaudz atšķirīgu shēmu, kas balstīta uz vērtību diapazonu. Piemēram, ja aplūkojam klases skolēnu augumu, biežumu tabula varētu izskatīties šādi.
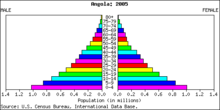
(Absolūtā) biežumu sadalījuma piemērs. Šī ir Angolas iedzīvotāju piramīda 2005. gadam.
Šī ir Ķīnas iedzīvotāju piramīda 2005. gadā.
Pieteikumi
Pārvaldīt un strādāt ar biežumu tabulārajiem datiem ir daudz vienkāršāk nekā strādāt ar neapstrādātiem datiem. Pastāv vienkārši algoritmi, lai no šīm tabulām aprēķinātu mediānu, vidējo vērtību (statistiku), standartnovirzi utt.
Statistikas hipotēžu pārbaude balstās uz frekvenču sadalījumu atšķirību un līdzību novērtēšanu. Šis novērtējums ietver centrālās tendences jeb vidējo lielumu mērījumus, piemēram, vidējo vērtību un mediānu, un mainīguma jeb statistiskās dispersijas mērījumus, piemēram, standartnovirzi vai dispersiju.
Biežumu sadalījumu uzskata par izkropļotu, ja tā vidējā vērtība un mediāna atšķiras. Biežumu sadalījuma kurtoze ir rezultātu koncentrācija pie vidējā rādītāja vai arī tas, cik maksimāli liels ir sadalījums, ja to attēlo grafiski, piemēram, histogrammā. Ja sadalījums ir ar lielāku maksimumu nekā normālais sadalījums, to sauc par leptokurtisku; ja sadalījums ir ar mazāku maksimumu, to sauc par platikurtisku.
Biežumu sadalījumu izmanto arī frekvenču analīzē, lai uzlauztu kodus, un tas attiecas uz burtu relatīvo biežumu dažādās valodās.
Jautājumi un atbildes
J: Kas ir frekvenču sadalījums?
A: Biežumu sadalījums ir saraksts ar mainīgā lieluma vērtībām izlasē, kas sakārtotas pēc daudzuma. Tas parāda, cik reizes parādās katra vērtība.
J: Kā varētu izskatīties piecu punktu Likerta skalas atbilžu biežuma sadalījums?
A: Atbildes biežuma sadalījums piecu punktu Likerta skalai var izskatīties kā vienkārša tabula, kurā norādīts to cilvēku skaits, kas novērtējuši katru skalas punktu.
J: Kādi ir divi trūkumi šāda veida tabulas izmantošanā?
A: Divi šāda veida tabulu izmantošanas trūkumi ir tādi, ka to var būt grūti vai pat neiespējami izmantot, ja runa ir par nepārtrauktām vērtībām vai ja ir pārāk daudz iespējamo vērtību.
J: Ar ko šī shēma atšķiras, ja runa ir par nepārtrauktām vērtībām vai lielu skaitu iespējamo vērtību?
A: Ja runa ir par nepārtrauktām vērtībām vai lielu skaitu iespējamo vērtību, var izmantot nedaudz atšķirīgu shēmu, kas balstīta uz vērtību diapazonu.
J: Kā varētu izskatīties skolēnu augstuma biežumu tabula?
A: Skolēnu augstuma biežumu tabulā varētu parādīt diapazonus un to, cik skolēnu ietilpst katrā diapazonā.
J: Kādu informāciju sniedz biežumu sadalījums?
A: Biežumu sadalījums sniedz informāciju par to, cik bieži izlasēs parādās konkrēti mainīgie lielumi un kā tie ir sadalīti šajās izlasēs.
