Standartnovirze: definīcija, aprēķins un nozīme statistikā
Standartnovirze: skaidra definīcija, praktiski aprēķini un nozīme statistikā — saprotami piemēri, interpretācija un izmantošana datu analīzē.
Standartnovirze ir skaitlis, ko izmanto, lai norādītu, kā grupas mērījumi atšķiras no vidējās) vai paredzamās vērtības. Zema standartnovirze nozīmē, ka lielākā daļa skaitļu ir tuvu vidējai vērtībai, bet liela standartnovirze norāda uz lielāku izkliedi un lielākām atšķirībām starp novērojumiem. Standartnovirze raksturo datus metriskā mērogā — tā norāda tipisko attālumu no vidējās vērtības un tiek plaši izmantota statistikā, pētījumos un finanšu analīzē.
Kā aprēķina standartnovirzi
Standartnovirze ir variances kvadrātsakne. Ir divi biežāk lietotie aprēķini:
- Populācijas standartnovirze (σ) — ja aprēķinam izmanto visus populācijas datus:
σ = sqrt( (1/N) * Σ (xi − μ)² )
kur N ir elementu skaits, xi — atsevišķie novērojumi, μ — populācijas vidējā vērtība. - Izlases (sample) standartnovirze (s) — ja izmanto paraugu, lai novērtētu populāciju, lieto Bessela koriģēto formulu:
s = sqrt( (1/(n−1)) * Σ (xi − x̄)² )
kur n ir parauga lielums un x̄ — parauga vidējā vērtība. Dalīšana ar (n−1) (nevis ar n) kompensē parauga izmantošanas kļūdu un dod neitrālu (nenovirzītu) variances novērtējumu.
Piemērs
Apskatīsim vienkāršu datu kopu: 2, 4, 4, 4, 5, 5, 7, 9.
- Vidējā (μ vai x̄) = (2+4+4+4+5+5+7+9) / 8 = 5.
- Atšķirības no vidējā: −3, −1, −1, −1, 0, 0, 2, 4.
- Kvadrāti: 9, 1, 1, 1, 0, 0, 4, 16; summa = 32.
- Populācijas dispersija = 32 / 8 = 4 → populācijas standartnovirze σ = sqrt(4) = 2.
- Izlases dispersija = 32 / (8−1) ≈ 4.571 → izlases standartnovirze s ≈ 2.138.
Interpretācija un nozīme
Standartnovirze norāda, cik plaši dati ir izkliedēti ap vidējo. Dažas svarīgas atziņas:
- Vienkāršs noteikums normālajai sadalījumam: aptuveni 68% vērtību būs intervālā ±1σ ap vidējo, aptuveni 95% — ±2σ, un ap 99.7% — ±3σ. Tieši no turienes nāk arī izteikums, ka "paziņotā kļūdas robeža parasti ir divreiz lielāka par standartnovirzi". Tomēr jāatceras, ka šī robeža attiecas uz novērojumu izkliedi populācijā;, ja runa ir par vidējās vērtības nenoteiktību, jālieto standarta kļūda (skat. zemāk).
- Zinātnieki bieži ziņo par datu standartnovirzi eksperimentos, jo tā parāda, cik liela ir mainība starp mērījumiem. Tomēr, lai raksturotu vidējā vērtības precizitāti, izmanto standarta kļūdu: SE = s / sqrt(n). 95% uzticamības intervāls vidējam aptuveni = x̄ ± 1.96·SE (pie nosacījuma par tuvu normālam sadalījumam).
- Naudas un finanšu kontekstā standartnovirze parāda atdeves svārstīgumu — lielāka standartnovirze nozīmē augstāku risku (lielāku cenu vai ienesīguma svārstīgumu) attiecībā pret vidējo ienesīgumu.
Izlases vs populācijas standartnovirze — kad kuru lietot
- Ja jums ir pieejami visi dati no visas populācijas (reti praksē), lietojiet populācijas formulu (dalīt ar N).
- Ja dati ir paraugs no lielākas populācijas — lietojiet izlases formulu (dalīt ar n−1), jo tā dod neizkropļotu variances novērtējumu.
- Dažādas programmatūras var pēc noklusējuma izmantot dažādas formulas — pārbaudiet, vai tā ir populācijas vai izlases standartnovirze.
Praktiski padomi un ierobežojumi
- Standartnovirze ir jutīga pret izliektiem novērojumiem (outliers). Dažos gadījumos labāk lietot robustākas mērvienības, piemēram, starpkvartilu atšķirību (IQR).
- Standartnovirze ir tāda pašā mērvienībā kā oriģinālie dati (atšķirībā no dispersijas, kas ir kvadrātā), tāpēc to ir vieglāk interpretēt praktiskās vienībās.
- Ja dati nav tuvu normālajam sadalījumam, procents vērtību intervālos ±1σ, ±2σ var būt ievērojami atšķirīgs no iepriekš minētā "68–95–99.7" likuma.
Kopsavilkums
Standartnovirze ir pamatmērījums, kas raksturo datu izkliedi ap vidējo. Izmantojiet populācijas formulu, ja aprēķinātie dati attiecas uz visu populāciju, un izlases formulu (ar Bessela koriģējumu) paraugiem. Lai raksturotu vidējā vērtības kļūdu, izmantojiet standarta kļūdu; lai novērtētu risku vai svārstīgumu (piem., finanšu lietās), izmantojiet standartnovirzi. Ja nepieciešams, varat papildināt ar robustām mērvienībām, ja dati satur izteiktus izņēmumus.
Daudzkārt var izmērīt tikai paraugu vai grupas daļu. Tad skaitli, kas ir tuvs visas grupas standartnovirzei, var atrast, izmantojot nedaudz atšķirīgu vienādojumu, ko sauc par izlases standartnovirzi, kā paskaidrots tālāk.
.png)
Normālā sadalījuma (jeb zvana līknes) diagramma. Katras krāsainās joslas platums ir viena standartnovirze.
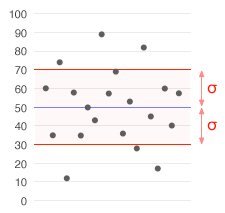
Datu kopa ar vidējo vērtību 50 (attēlots zilā krāsā) un standartnovirzi (σ) 20.
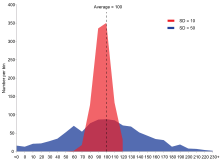
Piemērs divām izlases populācijām ar vienādu vidējo vērtību un dažādām standartnovirzēm. Sarkanajai populācijai ir vidējais 100 un SD 10; zilajai populācijai ir vidējais 100 un SD 50.
Pamata piemērs
Aplūkojiet grupu, kurā ir šādi astoņi skaitļi:
2 , , 44, 4, , 5, , 5, 7{\displaystyle9 2,\ 4,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9}
Šo astoņu skaitļu vidējā vērtība (vidējais) ir 5:
2 + +4 + + 4+ 4+ + 5+ + 5+ 7= 98{\displaystyle5 {\frac {2+4+4+4+4+5+5+7+9}{8}}}=5}
Lai aprēķinātu populācijas standartnovirzi, vispirms nosakiet katra saraksta skaitļa starpību no vidējā. Pēc tam katras starpības rezultātu kvadrātā:
( 2-5 ) =2 ( - 3) =2 ( 95- 5) =2 = = 02( 04-5 ) =2 ( - 1) = (15 - ) =2 ( - 5) =2 = 02( 04-5 ) =2 ( - 1) =2 (17 - 5) = 222( 44-5 ) = ( - ) = 2( -1 ) = 2( 19- 5) = = 2= 42{\displaystyle16 {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
Pēc tam atrodiet šo vērtību vidējo vērtību (summu daliet ar skaitļu skaitu). Visbeidzot, iegūstiet kvadrātsakni:
( +9 +1 + +1 +1 + + 0+ 0+ 4) 16= 8{\displaystyle2 {\sqrt {\frac {(9+1+1+1+1+1+0+0+0+4+16)}{8}}}}=2}
Atbilde ir populācijas standartnovirze. Formula ir pareiza tikai tad, ja astoņi skaitļi, ar kuriem mēs sākām, ir visa grupa. Ja tie ir tikai nejauši izvēlēta grupas daļa, tad priekšpēdējā soļa apakšā (saucējā) jāizmanto 7 (kas ir n - 1), nevis 8 (kas ir n). Tad atbilde ir izlases standartnovirze. To sauc par Besela korekciju.
Vairāk piemēru
Nedaudz sarežģītāks piemērs no reālās dzīves: Vidējais pieaugušu vīriešu augums ASV ir 70 cm, ar 3 cm standartnovirzi. Standartnovirze 3 collas nozīmē, ka lielākajai daļai vīriešu (aptuveni 68 %, pieņemot, ka sadalījums ir normāls) ir 3 collas lielāks līdz 3 collas mazāks augums nekā vidējais (67 - 73 collas) - viena standartnovirze. Gandrīz visu vīriešu (aptuveni 95 %) augums ir no 6" augstāks līdz 6" zemāks par vidējo (64"-76") - divas standartnovirzes. Trīs standartnovirzes ietver visus skaitļus 99,7 % no pētāmās izlases populācijas. Tas ir taisnība, ja sadalījums ir normāls (zvanveida).
Ja standartnovirze būtu nulle, tad visi vīrieši būtu precīzi 70" augumā. Ja standartnovirze būtu 20", tad daži vīrieši būtu daudz augstāki vai daudz zemāki par vidējo rādītāju, un tipiskais diapazons būtu aptuveni 50-90".
Vēl viens piemērs: katrai no trim grupām {0, 0, 14, 14}, {0, 6, 8, 14} un {6, 6, 8, 8} ir vidējais (vidējais) skaitlis 7. Bet to standartnovirzes ir 7, 5 un 1. Trešajai grupai ir daudz mazāka standartnovirze nekā pārējām divām, jo tās skaitļi ir tuvi 7. Pamatideja ir tāda, ka standartnovirze norāda, cik tālu no vidējā rādītāja mēdz būt pārējie skaitļi. Tai būs tādas pašas vienības kā pašiem skaitļiem. Ja, piemēram, grupa {0, 6, 8, 14} ir četru brāļu grupas vecums gados, tad vidējais ir 7 gadi un standartnovirze ir 5 gadi.
Standartnovirze var kalpot kā nenoteiktības mērs. Piemēram, zinātnē atkārtotu mērījumu grupas standartnovirze palīdz zinātniekiem noteikt, cik pārliecināti viņi ir par vidējo skaitli. Lemjot par to, vai eksperimenta mērījumi atbilst prognozēm, šo mērījumu standartnovirze ir ļoti svarīga. Ja eksperimentos iegūtais vidējais skaitlis ir pārāk tālu no prognozētā skaitļa (attālumu mēra standartnovirzēs), tad pārbaudāmā teorija var nebūt pareiza. Sk. prognozes intervālu.
Piemērošanas piemēri
Izpratne par vērtību kopuma standartnovirzi ir noderīga, lai zinātu, cik liela atšķirība no "vidējā" (vidējā) ir sagaidāma.
Laikapstākļi
Kā vienkāršu piemēru aplūkojiet divu pilsētu vidējo diennakts augstāko temperatūru - vienas pilsētas iekšzemē un otras - okeāna tuvumā. Ir lietderīgi saprast, ka pilsētām okeāna tuvumā diennakts augstās temperatūras amplitūda ir mazāka nekā pilsētām iekšzemē. Šajās divās pilsētās var būt vienāda vidējā dienas augstā temperatūra. Tomēr piekrastes pilsētas diennakts augstās temperatūras standartnovirze būs mazāka nekā iekšzemes pilsētā.
Sports
Vēl viens veids, kā to aplūkot, ir aplūkot sporta komandas. Jebkurā sporta veidā būs komandas, kas ir labas dažās jomās, bet citās - ne. Komandas, kas ierindojas augstākajās vietās, neuzrādīs lielas atšķirības spējās. Tām labi veicas lielākajā daļā kategoriju. Jo zemāka ir to spēju standartnovirze katrā kategorijā, jo līdzsvarotākas un saskaņotākas tās ir. Savukārt komandas ar lielāku standartnovirzi būs mazāk paredzamas. Komandai, kas parasti ir slikta lielākajā daļā kategoriju, būs zema standartnovirze. Komandai, kas parasti ir laba lielākajā daļā kategoriju, arī būs zema standartnovirze. Tomēr komanda ar augstu standartnovirzi var būt tāda komanda, kas gūst daudz punktu (spēcīgs uzbrukums), bet arī ļauj otrai komandai gūt daudz punktu (vāja aizsardzība).
Mēģinot iepriekš noskaidrot, kuras komandas uzvarēs, var apskatīt dažādu komandu "statistikas" standartnovirzes. Skaitļi, kas atšķiras no paredzamajiem, var salīdzināt stiprās un vājās puses, lai parādītu, kādi iemesli var būt vissvarīgākie, lai uzzinātu, kura komanda uzvarēs.
Sacīkstēs tiek mērīts laiks, kas braucējam nepieciešams, lai veiktu katru apli trasē. Braucējs ar mazu apļa laika standartnovirzi ir stabilāks nekā braucējs ar lielāku standartnovirzi. Šo informāciju var izmantot, lai saprastu, kā autovadītājs var samazināt laiku, kas vajadzīgs, lai pabeigtu apli.
Nauda
Naudā standartnovirze var nozīmēt risku, ka cena pieaugs vai samazināsies (akcijas, obligācijas, īpašums utt.). Tā var nozīmēt arī risku, ka cenu grupa palielināsies vai samazināsies (aktīvi pārvaldīti kopieguldījumu fondi, indeksu kopieguldījumu fondi vai ETF). Risks ir viens no iemesliem, kāpēc jāpieņem lēmums par to, ko iegādāties. Risks ir skaitlis, ko cilvēki var izmantot, lai uzzinātu, cik daudz naudas viņi var nopelnīt vai zaudēt. Riskam kļūstot lielākam, ieguldījuma ienesīgums var būt lielāks, nekā gaidīts ("plus" standartnovirze). Tomēr ieguldījums var arī zaudēt vairāk naudas, nekā gaidīts ("mīnus" standartnovirze).
Piemēram, personai bija jāizvēlas starp divām akcijām. Pēdējo 20 gadu laikā akcijas A vidējā peļņa bija 10 %, bet standarta novirze - 20 procentu punkti (pp). Akcijas B vidējā peļņa pēdējo 20 gadu laikā bija 12 %, bet standartnovirze bija lielāka - 30 procentu punkti. Pārdomājot risku, persona var izlemt, ka akcija A ir drošāka izvēle. Lai gan viņi, iespējams, neiegūs tik daudz naudas, viņi, visticamāk, arī daudz nezaudēs. Persona var uzskatīt, ka B akcijai par 2 procentpunktiem augstāks vidējais rādītājs nav vērts papildu 10 pp standarta novirzes (lielāks risks vai gaidāmās peļņas nenoteiktība).
Noteikumi par normāli sadalītiem skaitļiem
Lielākajā daļā matemātisko vienādojumu standartnovirzei tiek pieņemts, ka skaitļi ir sadalīti normāli. Tas nozīmē, ka skaitļi ir sadalīti noteiktā veidā abās vidējās vērtības pusēs. Normālo sadalījumu sauc arī par Gausa sadalījumu, jo to atklāja Karls Frīdrihs Gauss. To bieži sauc par zvanu līkni, jo skaitļi sadalās tā, ka grafikā iegūst zvanu formu.
Skaitļi nav normāli sadalīti, ja tie ir sagrupēti vienā vai otrā vidējās vērtības pusē. Skaitļi var būt izkliedēti, un tie joprojām ir normāli sadalīti. Standartnovirze norāda, cik plaši skaitļi ir izkliedēti.

Tumši zilā krāsā ir mazāk nekā viena standartnovirze no vidējā. Normālajam sadalījumam tas ietver 68,27 procentus skaitļu, savukārt divas standartnovirzes no vidējā (vidēja un tumši zila) ietver 95,45 procentus, trīs standartnovirzes (gaiši, vidēji un tumši zila) ietver 99,73 procentus, bet četras standartnovirzes - 99,994 procentus.
Attiecība starp vidējo (vidējo) un standartnovirzi
Datu kopas vidējo (vidējo) vērtību un standartnovirzi parasti raksta kopā. Tad cilvēks var saprast, kāds ir vidējais skaitlis un cik plaši ir izkliedēti citi skaitļi grupā.
To, kā sadalās skaitļu grupa, var noteikt arī ar variācijas koeficientu, kas ir standartnovirze, dalīta ar vidējo. Tas ir bezdimensiju skaitlis. Variāciju koeficientu bieži reizina ar 100 % un izsaka procentos.
Vēsture
Terminu standartnovirze pirmo reizi rakstiski lietoja Karls Pīrsons 1894. gadā pēc tam, kad viņš to lietoja lekcijās. Ar to tika aizstāti agrākie nosaukumi, kas apzīmēja to pašu ideju: piemēram, Gauss lietoja vidējo kļūdu.
Saistītās lapas
- Precizitāte un precizitāte
- Parauga lielums
Jautājumi un atbildes
J: Kas ir standartnovirze?
A: Standartnovirze ir skaitlis, ko izmanto, lai norādītu, cik lielā mērā kādas grupas mērījumi atšķiras no vidējās (vidējās vai paredzamās) vērtības.
J: Ko nozīmē zema standartnovirze?
A: Zema standartnovirze nozīmē, ka lielākā daļa skaitļu ir tuvu vidējai vērtībai.
J: Ko nozīmē liela standartnovirze?
A: Liela standartnovirze nozīmē, ka skaitļi ir vairāk izkliedēti.
J: Kā standartnovirzi izmanto naudā?
A: Naudā nopelnīto procentu standartnovirze parāda, cik atšķirīgi no vidējā rādītāja var būt vienas personas nopelnītie procenti.
J: Kad var izmērīt tikai daļu no grupas?
A: Daudzos gadījumos var izmērīt tikai paraugu vai grupas daļu.
J: Kā tiek attēlota visas grupas standartnovirze?
A: Visas grupas standartnovirzi apzīmē ar grieķu burtu َ {\displaystyle \sigma }. .
J: Kā tiek attēlota parauga standartnovirze?
A: Parauga standarta novirzi apzīmē ar s {\displaystyle s} .
Meklēt



