Varbūtības blīvuma funkcija
Varbūtības blīvuma funkcija ir funkcija, ko var definēt jebkuram nepārtrauktam varbūtības sadalījumam. Varbūtības blīvuma funkcijas integrālis intervālā [ a , b ] {\displaystyle [a,b]} ![{\displaystyle [a,b]}](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
dod varbūtību, ka dotais nejaušais mainīgais ar doto blīvumu atrodas dotajā intervālā.
Varbūtības blīvuma funkcija ir nepieciešama, lai varētu strādāt ar nepārtrauktiem sadalījumiem. Izmetot kauliņu, iegūsim skaitļus no 1 līdz 6 ar varbūtību 1 6 {\displaystyle {\tfrac {1}{6}}}. 
, bet tā nav nepārtraukta funkcija, jo iespējami tikai skaitļi no 1 līdz 6. Turpretī diviem cilvēkiem nebūs vienāds augums vai svars. Izmantojot varbūtības blīvuma funkciju, ir iespējams noteikt varbūtību cilvēkiem, kuru garums ir no 180 centimetriem līdz 181 centimetram vai no 80 kilogramiem līdz 81 kilogramam, lai gan starp šīm divām robežām ir bezgalīgi daudz vērtību.
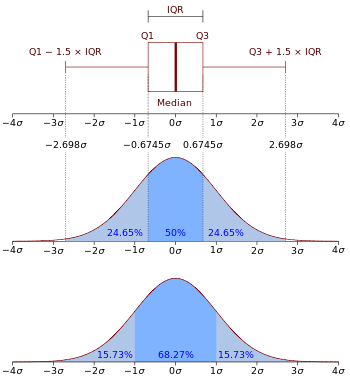
Normālā sadalījuma N(0, σ2) boksplots un varbūtības blīvuma funkcija.
Jautājumi un atbildes
J: Kas ir varbūtības blīvuma funkcija?
A: Varbūtības blīvuma funkcija ir funkcija, kas raksturo jebkuru nepārtrauktu varbūtības sadalījumu.
J: Kā raksta nejaušā lieluma X varbūtības blīvuma funkciju?
A: X varbūtības blīvuma funkciju dažreiz raksta kā f_X(x).
J: Ko attēlo varbūtības blīvuma funkcijas integrāls?
A: Varbūtības blīvuma funkcijas integrālis parāda varbūtību, ka dotais nejaušais lielums ar doto blīvumu atrodas dotajā intervālā.
Vai varbūtības blīvuma funkcija vienmēr ir nenegatīva visā tās apgabalā?
A: Jā, pēc definīcijas varbūtības blīvuma funkcija ir nenegatīva visā tās apgabalā.
Vai integrēšana intervālā summējas līdz 1?
A: Jā, integrēšana intervālā summējas līdz 1.
J: Kāda veida sadalījumu raksturo varbūtības blīvuma funkcija?
A: Varbūtības blīvuma funkcija raksturo jebkuru nepārtrauktu varbūtības sadalījumu.
