Varbūtība — definīcija, pamatprincipi un saprotami piemēri
Uzzini varbūtības definīciju, pamatprincipus un saprotamus piemērus — no monētām un kauliņiem līdz reāliem aprēķiniem, skaidri paskaidrojumi un praktiski piemēri ikdienai.
Varbūtība ir lietišķās matemātikas daļa. Tā nodarbojas ar nejaušību un pētījumiem par notikumiem, kas var vai var arī nenotikt — tīri teorētiski vai praksē, balstoties uz novērojumiem un eksperimentiem.
Piemēram, izmantojot varbūtības metodes, var parādīt, ka, ja met taisnīgu monētu daudzkārt, aptuveni puse no reizēm tai piezemēsies ar vienu pusi uz augšu, bet otra puse — ar otru. Uz daudzām monētām vienā pusē ir attēls ar kādas personas seju (to parasti sauc par "galvu"), bet otrā pusē — kāds zīmējums vai cipars ("astes"). Šis "puse laika" rezultāts ir teorētiska varbūtība gadījumā, ja monēta ir godīga; ilgtermiņa novērojumu tuvums teorētiskajai vērtībai saistīts ar lielo skaitu atkārtojumu (likums par lieliem skaitļiem).
Notikuma varbūtība (p) vienmēr ir no 0 (neiespējams) līdz 1 (droši). Piemēram: p=0 nozīmē, ka notikums nekad nenotiks; p=1 nozīmē, ka notikums vienmēr notiks.
Ja mēs metam kauliņu (daudzskaitlī: kauliņš), tad iespēja, ka uz tā būs 1, ir 1/6 (jo uz kauliņa ir 6 vienādi iespējami iznākumi). Tādējādi var teikt: iespēja uzmest jebkuru konkrētu skaitli no 1 līdz 6 ir 1/6, un iespēja uzmest kādu no skaitļiem 1–6 kopā ir 1 (jo viens no šiem iznākumiem noteikti notiks).
Pamatprincipi un biežāk lietotās formulas
- Klasiskā (vienādi iespējamo iznākumu) varbūtība: ja ir N vienādi iespējami iznākumi un tieši k no tiem atbilst notikumam A, tad P(A) = k / N.
- Komplementa likums: P(not A) = 1 − P(A). Tas izmanto to, ka vai nu notiek A, vai nenotiek A.
- Savienojuma (vai) likums diviem notikumiem: P(A vai B) = P(A) + P(B) − P(A un B). Ja notikumi ir izslēdzoši (mutuāli neatkarīgi gadījumā bez kopīgiem iznākumiem), tad P(A vai B) = P(A) + P(B).
- Reizināšanas likums (par kopīgu notikumu): ja notikumi A un B ir neatkarīgi, tad P(A un B) = P(A) × P(B). Ja nav neatkarīgi, izmanto nosacīto varbūtību (skat. zemāk).
- Nosacītā varbūtība: P(A | B) = P(A un B) / P(B), ja P(B) > 0. Šī formula apraksta varbūtību, ka notiek A, zinot, ka ir noticis B.
Praktiski piemēri
Divi metami kauliņi — konkrēta kombinācija. Iespēja uzmest 3 ar pirmo kauliņu ir 1/6, un iespēja uzmest 5 ar otro ir arī 1/6. Ja iznākumi ir neatkarīgi (katrs kauliņš neatkarīgs no otra), tad iespēja iegūt tieši 3 pēc tam 5 ir 1/6 × 1/6 = 1/36 ≈ 0,02778.
Trīs kauliņi — trīs konkrēti skaitļi. Iespēja iegūt, piemēram, 3, pēc tam 5, pēc tam 2 ir (1/6)^3 = 1/216 ≈ 0,00463.
Vismaz viens sešnieks divos kauliņos. Vieglākais veids aprēķinam: vispārējā varbūtība = 1 − P(neviens sešnieks). Iespēja, ka vienā kauliņā nav sešnieka, ir 5/6, abos kauliņos — (5/6)^2 = 25/36. Tātad iespēja vismaz vienam sešniekam = 1 − 25/36 = 11/36 ≈ 0,3056.
Kādēļ svarīgi saprast atšķirības
Ir dažas svarīgas atšķirības, ko vērts zināt:
- Teorētiskā varbūtība (piem., taisnīgas monētas vai godīga kauliņa gadījumā) balstās uz pieņēmumu par vienādi iespējamiem iznākumiem.
- Empīriskā (eksperimentālā) varbūtība tiek iegūta no novērojumiem: P(A) ≈ skaits reizes, kad notika A / kopējais novērojumu skaits. Ar lielu skaitu atkārtojumu empīriskās frekvences tuvinās teorētiskajām vērtībām (likums par lieliem skaitļiem).
- Neatkarība nozīmē, ka viena notikuma iznākums nekādi neietekmē otra varbūtību; ja tā nav, jārēķina nosacītās varbūtības.
Kā skaitīt iespējamās iznākumu skaitliskos uzdevumos
Lai pareizi aprēķinātu varbūtības, bieži jāzina, cik ir elementu iznākumu kopā (sample space) un cik no tiem atbilst interesējošajam notikumam. To dara, izmantojot kombinatorikas rīkus — permutations un kombinācijas — kad iznākumi nav vienkārši "vienā no N". Piemēram, izlozējot 2 kartes no 52, nevar vienkārši reizināt individuālās varbūtības, jo izvēles nav neatkarīgas; jālieto kombinatorikas skaitīšana vai nosacītā varbūtība.
Noslēgumā — svarīgākie punkti
- Varbūtība: skaitlis no 0 līdz 1, kas apraksta, cik reāli ir kāda notikuma iznākums.
- Galvenās formulas: P(A) = |A| / |Ω| (klasiskais gadījums), P(not A) = 1 − P(A), P(A un B) = P(A)·P(B) (ja neatkarīgi), P(A | B) = P(A un B)/P(B).
- Prakse un piemēri (metot monētu vai kauliņu) palīdz saprast teorētiskās formulas un to pielietojumu reālās situācijās.
Ja vēlaties, varu pievienot vairāk piemēru ar kartēm, kombinācijām vai reālās dzīves piemēriem (piem., medicīniskie testi, laika prognozes), vai arī sagatavot īsu uzdevumu komplektu ar risinājumiem, lai praktizētu šos principus.
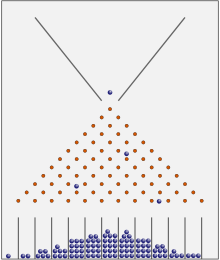
Pupiņu mašīnā vai Galtona kastē lielākā daļa bumbiņu nonāk tuvu centram. Ilgtermiņā tām būs normāls sadalījums.
Idejas par varbūtību
Tādi cilvēki kā Jakobs Bernuili, Pjērs Simons Laplašs vai Krišjāns Hīgenss lietoja vārdu "varbūtība", kā aprakstīts iepriekš. Citi cilvēki domāja par biežumiem; tur varbūtības jēdzienu parasti sauc par biežuma varbūtību.
Saistītās lapas
- Matemātikas tematu saraksts
- Varbūtību teorija
Jautājumi un atbildes
J: Kas ir varbūtība?
A: Varbūtība ir lietišķās matemātikas daļa, kas nodarbojas ar pētījumiem par lietām, kas var notikt vai var nenotikt.
J: Kā var izteikt varbūtību?
A: Varbūtību var izteikt kā skaitli no nulles (neiespējami) līdz vienai (droši).
J: Kāds ir varbūtības izmantošanas piemērs?
A: Piemēram, varbūtības izmantošanas piemērs ir parādīt, ka, metot monētu gaisā un ļaujot tai piezemēties, pusi no laika tā piezemēsies ar vienu pusi uz augšu, bet pusi no laika - ar otru pusi uz augšu.
J: Kā aprēķināt varbūtību, ka, metot divus metamos kauliņus, var iegūt noteiktu kombināciju?
A: Lai aprēķinātu divu kauliņu mešanas un noteiktas kombinācijas iegūšanas varbūtību, reiziniet abas to varbūtības kopā. Piemēram, ja vēlaties noskaidrot, cik liela ir iespēja, ka jums izdosies iegūt 3 un pēc tam 5, tas būtu 1/6 x 1/6 = 1/36.
J: Ko nozīmē "astes", runājot par monētām?
A: Runājot par monētām, "astes" apzīmē to pusi, uz kuras nav attēla.
Jautājums: Cik liela ir varbūtība, ka, metot sešus metamos kauliņus, var iegūt skaitli, kas lielāks par desmit? A: Iespējamību, ka, metot sešus metamos kauliņus, var iegūt skaitli, kas lielāks par desmit, var noteikt, izmantojot matemātiku un zinātni, taču tā nav acīmredzama.
J: Kas notiek, ja reizina divas varbūtības kopā?
A: Ja reizina divas varbūtības kopā, jūs aprēķināt iespēju, ka abas lietas notiks vienlaikus.
Meklēt