Kanoniski konjugētie mainīgie (Q, P): definīcija un nozīme kvantu mehānikā
Kanoniski konjugētie mainīgie Q un P: skaidrojums, Heizenberga–Borna komutators, vienādojumi un to nozīme kvantu mehānikā — jēdzieni, piemēri un pielietojumi.
Kanoniski konjugētie mainīgie kvantu mehānikā ir pāri operatoru (vai matricu) veidā, kuriem produktu kārtība ir nozīmīga — t.i., A•B parasti nav vienāds ar B•A. Šo īpašību sauc par nekomutatīvitāti. Praktiskā nozīmē tas nozīmē, ka, mērot vienu novērojamo lielumu un pēc tam otru, rezultāts var atšķirties, ja mērierīces secība tiek mainīta.
Heizenbergs un Borns: matricas mehānikas aizsākumi
Fiziķis Verners Heizenbergs izstrādāja kvantu mehānikas matricas formu, kurā novērojamās lielumi tiek attēloti kā matricas vai operatori. Heizenbergs atzina, ka impulss (parasti apzīmēts ar P) un pozīcija (apzīmēta ar Q) ir īpaša veida konjugētie lielumi — P un Q kā operatori nekonmutē: PQ ≠ QP. Šis atklājums ļāva aprakstīt kvantu sistēmas bez klasiskajiem trajektoriju jēdzieniem.
Heizenberga un viņa kolēģu formulējuma matricu elementu reizināšana tiek aprakstīta caur summām pār starpstāvokļu indeksiem. Piemēram, produktu elementu aprēķinā var uzrakstīt šādi:
Pirmo vienādojumu var izmantot, lai noskaidrotu momenta un pozīcijas reizinājumu:
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n-b)=\sum _{a}^{}\,p(n,n-a)q(n-a,n-b)}
Otro vienādojumu var izmantot, lai aprēķinātu pozīcijas un impulsa reizinājumu (šķirojot operatorus otrādākā secībā):
Z ( n , n - b ) = ∑ a q ( n , n - a ) p ( n - a , n - b ) {\displaystyle Z(n,n-b)=\sum _{a}^{}\,q(n,n-a)p(n-a,n-b)}
Šie vienādojumi parāda, ka produktu elementi atšķiras atkarībā no operatoru kārtības; tas ir pamats tam, kā matricu mehānika aprēķina pārejas starp enerģijas līmeņiem.
Borna formulējums: komutators un Planka konstante
Kā atklāja Makss Borns, šī kārtības atšķirība var tikt izteikta caur komutatoru. Komutators starp diviem operatoriem Q un P tiek definēts kā
[Q,P] = QP − PQ.
Borns parādīja, ka pozīcijas un impulsa komutators nav nulle, bet vienāds ar konstanti, kas saistīta ar Planka konstantu. To raksta arī kā
QP − PQ = iħ,
kur ħ (lasās kā "h svītra" jeb "reducētā Planka konstante") ir h / (2π), h ir Planka konstante, un i ir kompleksais vienības elements. Ekvivalenti var rakstīt arī precīzāk ar h:
Q*P-P*Q={\frac {ih}{2\pi }}
Šeit jāatzīmē, ka zīme "mīnuss" komutatorā ir parasts operatoru atņemšanas simbols — tas nav kā cits īpašs operators; komutators ir vienkārša operatoru atšķirība, [Q,P] = QP − PQ.
Fizikālā nozīme — nenoteiktības princips un kanoniskā kvantizācija
Kanonisko konjugēto mainīgo (piem., pozīcija un impulss) nekomutatīvitāte noved tieši pie Heizenberga nenoteiktības principa. Formāli tas izsakāms kā
ΔQ · ΔP ≥ ħ/2,
kas nozīmē: ja viena novērojamā lieluma mērījuma precizitāte pieaug (ΔQ kļūst maza), tad otrās precizitāte (ΔP) pamazām samazinās tā, lai šo lielumu precizitāšu reizinājs nevarētu būt mazāks par ħ/2. Tas nav tikai mērīšanas kļūda — tas ir fundamentāls kvantu sistēmas īpašums.
Kanoniskā kvantizācija parasti nozīmē klasiska pāra (q,p) Poasona komutatora {q,p}=1 aizstāšanu ar kvantu komutatoru [Q,P]=iħ. Šī procedūra ir pamats daudzām kvantu teorijas konstrukcijām (piem., kvantu lauka teorijā, harmoniskā oscilatora problēmā u.c.).
Piemērs: ūdeņraža atoms un spektru rindas
Konceptuāli Heizenberga matricu mehānika tika izmantota, lai aprakstītu, kā elektrons pāriet starp diskretiem enerģijas līmeņiem atomā un kā rodas fotonu emisija vai absorbcija. Attēlā redzams elektrona krišana no augstāka uz zemāku orbītu, emisijas rezultātā izdalot fotonu:
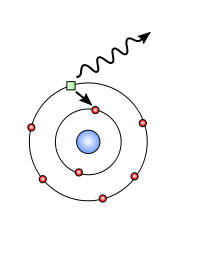
Kvantu mehānikā diskretie enerģijas līmeņi un pāreju iespējamības izriet no operatoru spektriem un to matricas elementiem — tieši no Heisenberga un Borna izveidotajām metodēm var iegūt ūdeņraža atomu spektru līnijas, kuras eksperimentāli novēro Emisijas/Absorbcijas spektroskopijā.
Nozīme plašākā kontekstā
- Konjugētie mainīgie un to komutatoru vienādojumi ir kvantu teorijas pamats — tie nosaka, kā klasiskās fizikas lielumi tiek "kvantizēti".
- Šī ideja ietekmē ne tikai fundamentālo fiziku, bet arī fizikas, ķīmijas un citu zinātņu jomu metodes (piem., molekulārā spektroskopija, kvantu ķīmija, kvantu informācija).
- Operatoru formāla rīcība ar matricām ļauj izmantot lineāro algebru un spektra teoriju, lai izpētītu kvantu sistēmu dinamiku un stabilus stāvokļus.
Kopsavilkumā: kanoniski konjugētie mainīgie, piemēram, pozīcija Q un impulss P, ir operatoru pāri ar īpašu komutatora attiecību [Q,P] = iħ. Šī nekomutatīvitāte ir pamatcēlonis kvantu daudzām atšķirībām no klasiskās fizikas — sākot ar nenoteiktības principu un beidzot ar kvantu enerģiju diskretizāciju un kvantu dinamiku aprakstu.
Dažas saistītas tēmas
Jautājumi un atbildes
J: Kas ir konjugētie mainīgie?
A: Konjugētie mainīgie ir īpaši mainīgo pāri (piemēram, x, y, z), kas, veicot ar tiem noteiktu matemātisku darbību, nedod vienādu rezultātu. Tas nozīmē, ka x*y nav vienāds ar y*x.
J: Kas atklāja konjugētos mainīgos?
A: Fiziķis Verners Heizenbergs un viņa kolēģi izmantoja klasiskajā fizikā pētītos vienādojumus, lai aprakstītu un prognozētu notikumus kvantu fizikā. Viņš atklāja, ka impulss (masa reizināta ar ātrumu, ko apzīmē ar P) un pozīcija (ko apzīmē ar Q) ir konjugēti lielumi.
Kādu vienādojumu var izmantot, lai aprēķinātu impulsa un pozīcijas reizinājumu?
A: Pirmo vienādojumu var izmantot, lai noskaidrotu impulsa un pozīcijas reizinājumu: Y(n,n-b)=∑a p(n,n-a)q(n-a,n-b).
J: Kādu vienādojumu var izmantot, lai aprēķinātu pozīcijas un impulsa reizinājumu?
A: Lai aprēķinātu pozīcijas un impulsa reizinājumu, var izmantot otro vienādojumu: Z(n,n-b)=∑a q(n,n-a)p(n-a, n-b).
J: Ko Makss Borns atklāja par konjugētajiem mainīgajiem?
A: Makss Born atklāja, ka, tā kā P*Q nav vienāds ar Q*P, rezultāts Q*P mīnus P*Q nav nulle. Viņš arī atklāja, ka Q-P - P-Q = ih/2π.
J: Kā Plankas konstante parādās kvantu mehānikā?
A: Plankas konstante daudz parādās kvantu mehānikā, jo tā parādās Maksa Borna vienādojumā konjugēto mainīgo reizinājumu aprēķināšanai; konkrēti kā h/2π vienā pusē no vienādības zīmes.
J: Kādās jomās konjugētie mainīgie ir pielietojami?
A: Konjugētie mainīgie ir pielietojami visā fizikā, ķīmijā un citās zinātnes jomās.
Meklēt


