Heizenberga nenoteiktības princips

Apjukums ar novērotāja efektu

Vēsturiski nenoteiktības princips ir sajaukts ar nedaudz līdzīgu efektu fizikā, ko sauc par novērotāja efektu. Tas saka, ka dažu sistēmu mērījumus nevar veikt, neietekmējot sistēmas. Heizenbergs piedāvāja šādu novērotāja efektu kvantu līmenī kā kvantu nenoteiktības fizikālu "skaidrojumu".

Tomēr tagad ir skaidrs, ka nenoteiktības princips ir visu viļņveida sistēmu īpašība. Tas rodas kvantu mehānikā vienkārši tāpēc, ka visiem kvantu objektiem piemīt matērijas viļņu raksturs. Tādējādi nenoteiktības princips patiesībā nosaka kvantu sistēmu fundamentālu īpašību, nevis apgalvojumu par pašreizējās tehnoloģijas novērojumiem. "Mērījums" nenozīmē tikai procesu, kurā piedalās fiziķis-novērotājs, bet gan jebkuru mijiedarbību starp klasiskajiem un kvantu objektiem neatkarīgi no kāda novērotāja.

Ideja par nenoteiktību

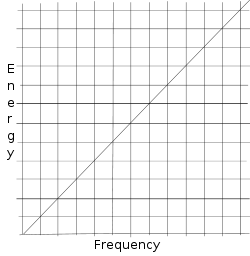
Nenoteiktības princips radās Vernera Heizenberga matricu mehānikā. Makss Planks jau zināja, ka gaismas vienības enerģija ir proporcionāla šīs gaismas vienības frekvencei ( E ∝ ν {\displaystyle E\propto \nu } ) un ka tās enerģijas daudzumu var izteikt pazīstamos terminos, piemēram, džoulā, izmantojot proporcionalitātes konstanti. Konstanti, ko viņš deva pasaulei, tagad sauc par Planka konstanti, un to apzīmē ar burtu h. Kad kvantu mehānikas izteikšanai izmanto matricas, bieži vien ir jāreizina divas matricas, lai iegūtu trešo matricu, kas dod atbildi, kuru fiziķis mēģina atrast. Bet, reizinot matricu, piemēram, P (impulsa momentam), ar matricu, piemēram, X (pozīcijai), iegūst citu atbildes matricu nekā tad, ja reizina X ar P. Rezultātā, reizinot P ar X un X ar P un pēc tam salīdzinot tos, vienmēr kā faktors ir Planka konstante. Plankas konstantes rakstīšanai izmantotais skaitlis vienmēr būs atkarīgs no izmantotās mērīšanas sistēmas. (Ar noteiktu mērīšanas sistēmu tās skaitliskā vērtība ir viens.) No izvēlētās mērīšanas sistēmas būs atkarīgs arī diagrammā pa labi redzamās līnijas slīpums, kas parāda frekvences un enerģijas attiecību.

Nākamajās diagrammās parādīts, kas notiek, ja mēs mēģinām izmērīt gan atrašanās vietu, gan impulsu.

Šī matemātiskā atklājuma praktiskais rezultāts ir tāds, ka tad, kad fiziķis precizē pozīciju, tad impulss kļūst mazāk skaidrs, un tad, kad fiziķis precizē impulsu, tad pozīcija kļūst mazāk skaidra. Heizenbergs teica, ka lietas ir "nenoteiktas", un citi cilvēki mīlēja teikt, ka tās ir "nenoteiktas". Taču matemātika rāda, ka tieši lietas pasaulē ir nenoteiktas jeb "neskaidras", nevis tikai cilvēki ir neskaidri par notiekošo.

Plašs atvērums, ass fokuss


Samazinot atstarpi, palielinās pārliecība par to, kur fotons atrodas vidū, bet tad tā virziens no turienes uz atklāšanas ekrānu labajā pusē kļūst attiecīgi nenoteiktāks.


Šaurs caurums, izkliedēts fokuss


Centra spraugas piekāršana ar atsperēm ļauj izmērīt impulsu, bet neparedzami pārvieto spraugu, tāpēc informācija par fotona atrašanās vietu vidū tiek zaudēta.


Uz atsperes uzstādīts caurums mēra impulsu

Nenoteiktības izteikšana matemātiskā formā

Šeit mēs parādīsim pirmo vienādojumu, kas sniedza pamatideju, kas vēlāk tika parādīta Heizenberga nenoteiktības principā.

Heizenberga 1925. gada revolucionārajā darbā nav izmantotas un pat nav minētas matricas. Heizenberga lielais panākums bija "shēma, kas principā spēja viennozīmīgi noteikt attiecīgās ūdeņraža starojuma fizikālās īpašības (pārejas frekvences un amplitūdas)".

Pēc tam, kad Heizenbergs bija uzrakstījis savu izšķirošo darbu, viņš to atdeva vienam no saviem skolotājiem, lai to sakārto, un devās atvaļinājumā. Makss Borns bija neizpratnē par vienādojumiem un nekomutējošiem vienādojumiem, kas pat Heizenbergam šķita problemātiski. Pēc vairākām dienām Borns saprata, ka šie vienādojumi ir norādījumi matricu izrakstīšanai. Matricas bija jaunas un dīvainas pat tā laika matemātiķiem, taču to, kā ar tām rēķināt, jau bija skaidri zināms. Pirms Heizenbergs atgriezās no atvaļinājuma, viņš kopā ar dažiem citiem visu izstrādāja matricas formā, un dažu mēnešu laikā jaunā kvantu mehānika matricas formā deva pamatu vēl vienam darbam.

Makss Borns redzēja, ka, aprēķinot pq un qp raksturojošās matricas, tās nebūs vienādas. Heizenbergs jau bija saskatījis to pašu, ņemot vērā viņa sākotnējo lietu pieraksta veidu, un Heizenbergs, iespējams, nojauta to, kas Bornam bija gandrīz uzreiz acīmredzams - ka starpība starp atbilžu matricām pq un qp vienmēr būs saistīta ar diviem koeficientiem, kas izrietēja no Heizenberga sākotnējās matemātikas: Plankas konstante h un i, kas ir kvadrātsakne no negatīvā vienāda. Tātad pati ideja par to, ko Heizenbergs labprātāk sauca par "nenoteiktības principu" (parasti pazīstams kā nenoteiktības princips), slēpās Heizenberga sākotnējos vienādojumos.

Heizenbergs pētīja izmaiņas, kas notiek atomos, kad elektrons maina enerģijas līmeni un tādējādi pietuvojas atoma centram vai attālinās no tā, un īpaši situācijas, kad elektrons divos soļos nokrīt uz zemāku enerģijas stāvokli. Makss Borns paskaidroja, kā viņš izmantoja Heizenberga dīvaino "recepti", lai atrastu kādas izmaiņas atomā no enerģijas līmeņa n uz enerģijas līmeni n-b reizinājumu C, kas ietvēra summu, ko iegūst, reizinot vienu pārmaiņu, ko sauc par A (kas varētu būt, piemēram, kāda fotona frekvence), ko izraisa elektronu enerģijas maiņa atomā no enerģijas stāvokļa n uz enerģijas stāvokli n-a), ar nākamo pārmaiņu, ko sauc par B (kas varētu būt, piemēram, pārmaiņu amplitūda), ko izraisa cita enerģijas stāvokļa maiņa no n-a uz n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

un atklāja kaut ko revolucionāru:

Aplūkojot ...piemērus... [Heizenbergs] atrada šo noteikumu..... Tas bija 1925. gada vasarā. Heizenbergs... paņēma atvaļinājumu... un nodeva savu darbu man publicēšanai....

Heizenberga reizināšanas likums man nedeva miera, un pēc nedēļas intensīvu pārdomu un izmēģinājumu, es pēkšņi atcerējos algebras teoriju....Tādus kvadrātveida masīvus matemātiķi diezgan labi pazīst un sauc par matricām, kopā ar noteiktu reizināšanas noteikumu. Es piemēroju šo noteikumu Heizenberga kvantu nosacījumam un atklāju, ka tas atbilst diagonāles elementiem. Bija viegli uzminēt, kādiem jābūt pārējiem elementiem, proti, nulles elementiem, un uzreiz manā priekšā bija dīvainā formula

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
[Simbols Q ir pārvietojuma matrica, P ir impulsa matrica, i apzīmē kvadrātsakni no negatīvā, bet h ir Planka konstante.]

Vēlāk Heizenbergs savu atklājumu noformulēja citā matemātiskā formā:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}}

(Īpašais simbols ℏ {\displaystyle {\hbar }} tiek saukts par "h-bar" jeb "reducēto Planka konstanti" un ir vienāds ar h 2 π {\displaystyle {\frac {h}{2\pi }}} .)

Matemātika ir veids, kā aprakstīt lietas, kas notiek reālajā pasaulē. Varētu iedomāties, ka būtu viegli vienlaikus iegūt gan precīzu kaut kā atrašanās vietu, gan precīzu masu, ceļu un ātrumu. Tomēr realitātē, lai iegūtu atbildi, ir jāveic divas lietas. Ja jūs mērojat lodes, kas iestrēgusi kāda liela kalna klintī, atrašanās vietu un kustības momentu, tas ir vienkāršs uzdevums. Kalns nešķiet, ka kaut kur virzās, un nešķiet, ka arī lode virzās. Tātad tās atrašanās vieta ir zināma, un tās ātrums ir 0, tātad arī impulss ir 0. Bet, ja lode atrodas kaut kur starp šauteni un mērķi, būs grūti noteikt tās atrašanās vietu jebkurā brīdī. Labākais, ko mēs varam izdarīt, ir nofotografēt lodi, izmantojot kameru ar ļoti ātru slēdžu. Taču, vienreiz nospiežot slēdžu, var iegūt tikai vienu informāciju - lodes pozīciju laikā t. Lai iegūtu impulsu, mēs varētu ielikt lodes ceļā parafīna bloku un izmērīt, kā parafīna bloks pārvietojas, kad tas aptur lodi. Vai arī, ja mēs zinātu lodes masu, mēs varētu uzņemt divu attēlu secību, aprēķināt ātrumu, zinot starpību starp divām lodes pozīcijām un laiku starp abām tās parādīšanās reizēm. Lai kā mēs to darītu, mums ir jāmēra masa, pozīcija un laiks starp parādīšanās reizēm. Beigu beigās mēs veiksim vismaz divus mērījumus, lai iegūtu x un p. Tādā gadījumā mums jāizvēlas, kuru mērījumu veikt vispirms un kuru vēlāk. Šķiet, ka nav nozīmes, kādā secībā tiek veikti mērījumi. Vai nu izmērīt lodes masu un pēc tam divreiz izmērīt tās pozīcijas, vai divreiz izmērīt lodes pozīcijas un pēc tam atgūt lodi un izmērīt tās masu, tas neko nemainītu, vai ne? Galu galā, svēršanas vai fotografēšanas laikā mēs ar lodi neko neesam darījuši.

Tomēr ļoti mazā mērogā, kad mēs mēra kaut ko tādu kā elektronu, katrs mērījums kaut ko ar to dara. Ja mēs vispirms izmērām pozīciju, tad šajā procesā mēs izmainām tā momemtumu. Ja mēs vispirms izmērām elektrona impulsu, tad šajā procesā mēs mainām tā pozīciju. Mūsu cerība būtu izmērīt vienu no tiem un pēc tam izmērīt otru, pirms kaut kas mainās, bet mūsu mērīšana pati par sevi rada izmaiņas, un labākais, uz ko mēs varam cerēt, ir līdz minimumam samazināt enerģiju, ko mēs dodam elektronam, to mērot. Šim minimālajam enerģijas daudzumam viens no faktoriem ir Planka konstante.

Nenoteiktība sniedzas tālāk par matricas matricu

Heizenberga nenoteiktības princips bija atrodams "jaunās" kvantu fizikas pirmajos vienādojumos, un teorija tika dota, izmantojot matricu matemātiku. Tomēr nenoteiktības princips ir fakts par dabu, un tas parādās arī citos kvantu fizikas veidos, piemēram, Ervina Šrēdingera vienādojumos.

Dabas nenoteiktība, nevis cilvēku nenoteiktība

Heizenberga atklājumi ir aplūkoti divos ļoti atšķirīgos veidos: Daži cilvēki uzskata, ka dabā notiekošais ir "determinēts", proti, viss notiek pēc noteikta likumsakarības, un, ja mēs varētu zināt visu, kas mums jāzina, mēs vienmēr varētu pateikt, kas notiks tālāk. Citi cilvēki domā, ka dabā notiekošās lietas nosaka tikai varbūtība, un mēs varam zināt tikai to, kā lietas uzvedīsies vidēji - bet mēs to zinām ļoti precīzi.

Fiziķis Džons Stjuarts Bells atklāja veidu, kā pierādīt, ka pirmais veids nevar būt pareizs. Viņa darbu sauc par Bella teorēmu jeb Bella nevienādību.

Populārā kultūra

Ar izteicienu "kvantu lēciens" vai "kvantu lēciens" tiek saprastas lielas un pārveidojošas pārmaiņas, un politiķi un plašsaziņas līdzekļu pārdošanas kampaņas to bieži izmanto hiperboliskos izteicienos. Kvantu mehānikā to lieto, lai aprakstītu elektrona pāreju no vienas orbītas ap atoma kodolu uz jebkuru citu orbītu, augstāku vai zemāku.

Dažkārt vārds "quantum" tiek lietots komerciālu produktu un uzņēmumu nosaukumos. Piemēram, Briggs and Stratton ražo daudzus mazo benzīna dzinēju veidus zāles pļaujmašīnām, rotējošiem kultivatoriem un citām mazām mašīnām. Viens no to modeļu nosaukumiem ir "Quantum".

Tā kā nenoteiktības princips nosaka, ka noteiktus mērījumus atomu līmenī nevar veikt, netraucējot citus mērījumus, daži cilvēki izmanto šo ideju, lai aprakstītu gadījumus cilvēku pasaulē, kad novērotāja darbība maina novērojamo lietu. Antropologs var doties uz kādu tālu vietu, lai uzzinātu, kā tur dzīvo cilvēki, bet fakts, ka viņus vēro svešs cilvēks no ārpasaules, var mainīt šo cilvēku rīcību.

Tas, ko cilvēki dara, vērojot lietas, kas maina novērojamo, ir novērotāja efekta gadījumi. Dažas lietas, ko cilvēki dara, izraisa izmaiņas ļoti mazā atomu līmenī, un tās ir nenoteiktības jeb nenoteiktības gadījumi, kā pirmais aprakstīja Heizenbergs. Nenoteiktības princips rāda, ka vienmēr pastāv robeža, cik mazus mērījumu pārus, piemēram, pozīcijas un ātruma vai trajektorijas un impulsa, mēs varam veikt. Novērotāja efekts saka, ka dažkārt tas, ko cilvēki dara, novērojot lietas, piemēram, uzzinot par skudru koloniju, izrakņājot to ar dārza rīkiem, var radīt lielu ietekmi, kas maina to, ko viņi mēģināja uzzināt.