Planka konstante

Fons

Šajā rakstā izmantotie simboli.
Simbols Nozīme E Enerģija h Planka konstante k Bolcmaņa konstante c gaismas ātrums λ starojuma viļņa garums ν starojuma frekvence T absolūtā temperatūra

No 1670. līdz 1900. gadam zinātnieki diskutēja par gaismas dabu. Daži zinātnieki uzskatīja, ka gaisma sastāv no daudziem miljoniem sīku daļiņu. Citi zinātnieki uzskatīja, ka gaisma ir vilnis.

Gaisma: viļņi vai daļiņas?

1678. gadā Kristjans Hīgenss sarakstīja grāmatu "Traktāts par gaismu" ("Traité de la lumiere"). Viņš uzskatīja, ka gaisma sastāv no viļņiem. Viņš apgalvoja, ka gaisma nevar sastāvēt no daļiņām, jo gaisma no diviem stariem viens no otra neatraujas. 1672. gadā Īzaks Ņūtons uzrakstīja grāmatu "Optika. Viņš uzskatīja, ka gaisma sastāv no sarkanām, dzeltenām un zilām daļiņām, kuras viņš sauca par korpuskulām. Ņūtons to izskaidroja ar savu "divu prizmu eksperimentu". Pirmā prizma sadalīja gaismu dažādās krāsās. Otrā prizma šīs krāsas atkal apvienoja baltā gaismā.

18. gadsimtā vislielākā uzmanība tika pievērsta Ņūtona teorijai. 1803. gadā Tomass Jangs (Thomas Young) aprakstīja "dubultšķautnes eksperimentu". Šajā eksperimentā gaisma, kas iet caur divām šaurām spraugām, interferē pati ar sevi. Tas rada zīmējumu, kas parāda, ka gaisma sastāv no viļņiem. Līdz 19. gadsimta beigām vislielākā uzmanība tika pievērsta gaismas viļņu teorijai. 1860. gados Džeimss Klerks Maksvels izstrādāja vienādojumus, kas aprakstīja elektromagnētisko starojumu kā viļņus.

Elektromagnētiskā starojuma teorijā gaisma, radioviļņi, mikroviļņi un daudzi citi viļņu veidi tiek uzskatīti par vienu un to pašu, tikai ar atšķirīgu viļņu garumu. Gaismas viļņa garums, ko mēs redzam ar savām acīm, ir aptuveni no 400 līdz 600 nm. Radioviļņu viļņa garums ir no 10 m līdz 1500 m, bet mikroviļņu viļņa garums ir aptuveni 2 cm. Vakuumā visi elektromagnētiskie viļņi pārvietojas ar gaismas ātrumu. Elektromagnētiskā viļņa frekvenci nosaka:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}}.

Šeit ir definēti simboli.

Melni korpusa radiatori

Visas siltas lietas izstaro siltuma starojumu, kas ir elektromagnētiskais starojums. Lielākajai daļai lietu uz Zemes šis starojums ir infrasarkanajā diapazonā, bet kaut kas ļoti karsts (1000 °C vai vairāk) izstaro redzamo starojumu, t. i., gaismu. XIX gadsimta beigās daudzi zinātnieki pētīja elektromagnētiskā starojuma viļņu garumus, ko rada melnā ķermeņa radiatori dažādās temperatūrās.

Rayleigh-Jeans likums

Lords Reilijs pirmo reizi publicēja Reilija-Džeinsa likuma pamatus 1900. gadā. Šīs teorijas pamatā bija gāzu kinētiskā teorija. Sers Džeinss Džeinss 1905. gadā publicēja pilnīgāku teoriju. Likums nosaka elektromagnētiskās enerģijas daudzumu un viļņa garumu, ko dažādās temperatūrās izstaro melna ķermeņa radiators. To raksturo šāds vienādojums:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}}.

Attiecībā uz liela viļņa garuma starojumu ar šo vienādojumu paredzētie rezultāti labi atbilda laboratorijā iegūtajiem praktiskajiem rezultātiem. Tomēr īsiem viļņu garumiem (ultravioletā gaisma) atšķirība starp teoriju un praksi bija tik liela, ka tā izpelnījās iesauku "ultravioletā katastrofa".

Planka likums

1895. gadā Vīns publicēja savu pētījumu rezultātus par melnā ķermeņa starojumu. Viņa formula bija šāda:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Šī formula labi darbojās īsviļņu elektromagnētiskā starojuma gadījumā, bet nedarbojās labi garu viļņu gadījumā.

1900. gadā Makss Planks publicēja savu pētījumu rezultātus. Viņš mēģināja izstrādāt melnā ķermeņa starojuma izteiksmi, kas izteikta ar viļņa garumu, pieņemot, ka starojums sastāv no maziem kvantiem, un pēc tam noskaidrot, kas notiek, ja kvantus padara bezgalīgi mazus. (Tā ir standarta matemātiska pieeja). Izteiciens bija šāds:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={{\frac {2hc^{2}}{\lambda ^{5}}}}~~{\frac {1}{e^{\frac {hc}{\lambda kT}}}-1}}}}.

Ja gaismas viļņa garums var kļūt ļoti liels, tad var pierādīt, ka Reilija-Džeinsa un Planka sakarības ir gandrīz identiskas.

Viņš aprēķināja h un k un konstatēja, ka

h = 6,55 × 10⁻²⁷erg-sek.

k = 1,34 × 10⁻¹⁶erg-deg ^-1.

Šīs vērtības ir tuvas mūsdienās pieņemtajām vērtībām, kas ir ⁻¹⁶attiecīgi 6,62606×10⁻³⁴ un 1,38065×10. Planka likums labi saskan ar eksperimentālajiem datiem, taču tā nozīme pilnībā tika novērtēta tikai pēc vairākiem gadiem.

Gaismas kvantu teorija

Izrādās, ka elektroni tiek izkliedēti ar fotoelektriskā efekta palīdzību, ja gaisma sasniedz robežfrekvenci. Zem šīs frekvences no metāla nevar izdalīties elektroni. Alberts Einšteins 1905. gadā publicēja darbu, kurā izskaidroja šo efektu. Einšteins ierosināja, ka gaismas stars nav vilnis, kas izplatās telpā, bet gan diskrētu viļņu pakešu (fotonu) kopums, no kuriem katram ir enerģija. Einšteins apgalvoja, ka efekts radies fotona trieciena rezultātā ar elektronu. Tas pierādīja gaismas daļiņu dabu.

Einšteins arī atklāja, ka elektromagnētiskais starojums ar lielu viļņa garumu nav iedarbīgs. Einšteins apgalvoja, ka tas ir tāpēc, ka "daļiņām" nav pietiekami daudz enerģijas, lai traucētu elektronus.

Planks ierosināja, ka katra fotona enerģija ir saistīta ar fotona frekvenci, izmantojot Planka konstanti. Matemātiski to varētu izteikt matemātiski šādi:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}}.

Planks 1918. gadā saņēma Nobela prēmiju par nopelniem fizikas attīstībā, atklājot enerģijas kvantus. Einšteins 1921. gadā saņēma Nobela prēmiju par Plankas konstantes saistīšanu ar fotoelektrisko efektu.

Ilustrācija ņemta no Ņūtona oriģinālās vēstules Karaliskajai biedrībai (1671. gada 1. janvāris [Jūlija kalendārs]). S attēlo saules gaismu. Gaisma starp plaknēm BC un DE ir krāsaina. Šīs krāsas tiek rekombinētas, veidojot saules gaismu plaknē GH.


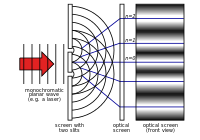
Janga dubultās spraugas eksperiments


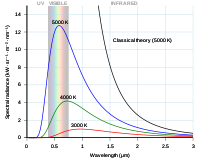
Reilija-Džeinsa līkne un Plankas līkne, kas attēlota atkarībā no fotona viļņa garuma.


Solveja konference 1911. gadā. Planks, Einšteins un Džeinss stāv. Planks ir otrais no kreisās. Einšteins ir otrais no labās puses. Džinss ir piektais no labās puses. Vīns sēž, trešais no labās puses.

Pieteikums

Planka konstantei ir liela nozīme daudzos lietojumos. Dažas no tām ir uzskaitītas turpmāk.

Bora atoma modelis

1913. gadā Nilss Bors publicēja Bora atoma struktūras modeli. Bors apgalvoja, ka elektronu leņķiskais moments, kas riņķo ap kodolu, var būt tikai noteiktas vērtības. Šīs vērtības nosaka vienādojums

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

kur

L = leņķiskais moments, kas saistīts ar līmeni.

n = pozitīvs vesels skaitlis.

h = Planka konstante.

Lai aprēķinātu elektronu enerģiju katrā līmenī, var izmantot Bora atoma modeli. Parasti elektroni aizpilda atoma zemākos līmeņus. Ja atoms saņem enerģiju, piemēram, no elektriskās strāvas, elektroni tiek ierosināti uz augstāku stāvokli. Pēc tam elektroni nokritīs atpakaļ uz zemāku stāvokli un zaudēs savu papildu enerģiju, izdalot fotonu. Tā kā enerģijas līmeņiem ir noteiktas vērtības, arī fotoniem būs noteikti enerģijas līmeņi. Šādi izstarotu gaismu var sadalīt dažādās krāsās, izmantojot prizmu. Katram elementam ir savs modelis. Neona modelis ir parādīts blakus.

Heizenberga nenoteiktības princips

1927. gadā Verners Heizenbergs publicēja nenoteiktības principu. Šis princips nosaka, ka nav iespējams veikt mērījumu, netraucējot mērāmo objektu. Tas arī nosaka robežu minimālajam traucējumam, ko izraisa mērījuma veikšana.

Makroskopiskajā pasaulē šiem traucējumiem ir ļoti maza ietekme. Piemēram, ja tiek mērīta temperatūra kolbā ar šķidrumu, termometrs uzkarstot absorbē nelielu enerģijas daudzumu. Tas radīs nelielu kļūdu galīgajā rādījumā, taču šī kļūda ir neliela un nav svarīga.

Kvantu mehānikā ir citādi. Daži mērījumi tiek veikti, aplūkojot izkliedēto fotonu modeli. Viens no šādiem piemēriem ir Komptona izkliedēšana. Ja mēra gan daļiņas pozīciju, gan impulsu, nenoteiktības princips nosaka, ka pastāv kompromiss starp precizitāti, ar kādu tiek mērīts impulss, un precizitāti, ar kādu tiek mērīta pozīcija. Vienādojums, kas apraksta šo kompromisu, ir šāds:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad }

kur

Δp = impulsa nenoteiktība.

Δx = pozīcijas nenoteiktība.

h = Planka konstante.

Gaismu izstarojošo diodžu krāsa

Labajā attēlā redzamajā elektriskajā ķēdē sprieguma kritums gaismas diodē (LED) ir atkarīgs no LED materiāla. Silīcija diodēm šis kritums ir 0,6 V, bet gaismas diodēm tas ir no 1,8 V līdz 2,7 V. Šī informācija ļauj lietotājam aprēķināt Planka konstanti.

Enerģija, kas nepieciešama, lai viens elektrons pārlēktu potenciālo barjeru LED materiālā, ir atkarīga no lieluma

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

kur

Q_e ir viena elektrona lādiņš.

V_L ir sprieguma kritums gaismas diodē.

Kad elektrons atkal sadalās, tas izstaro vienu gaismas fotonu. Fotona enerģiju nosaka tas pats vienādojums, ko izmanto fotoelektriskajā efektā. Ja šos vienādojumus apvieno, gaismas viļņa garums un spriegums ir saistīti ar šādu formulu

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}},}

No šīs sakarības var aprēķināt tālāk redzamo tabulu.

Krāsa	Viļņa garums (nm)	Spriegums
sarkanā gaisma	650	1.89
zaļā gaisma	550	2.25
zilā gaisma	470	2.62

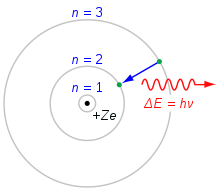
Bora atoma modelis. Elektrons, kas no n=3 čaulas nokrīt uz n=2 čaulu, zaudē enerģiju. Šī enerģija tiek pārnesta kā viens fotons.


Neona redzamais spektrs. Katra līnija attēlo atšķirīgu enerģijas līmeņu pāri.


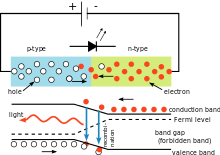
Vienkārša LED shēma, kas ilustrē Planka konstantes izmantošanu. Izstarotās gaismas krāsa ir atkarīga no sprieguma krituma pāri diodei. Gaismas viļņa garumu var aprēķināt, izmantojot Planka konstanti.

Plankas konstantes vērtība un kilograma pārdefinīcija

Kopš tā atklāšanas h mērījumi ir kļuvuši daudz labāki. Planks pirmais noteica, ka h vērtība ir 6,55 × 10 ⁻²⁷erg-sek. Šī vērtība ir 5 % robežās no pašreizējās vērtības.

Uz 2014. gada 3. martu labākais h mērījums SI vienībās ir 6,62606957×10 ⁻³⁴J-s. Ekvivalents skaitlis Cgs vienībās ir 6,62606957×10 ⁻²⁷erg-sec. Relatīvā h nenoteiktība ir 4,4 × 10 ⁻⁸.

Samazinātā Planka konstante (ħ) ir vērtība, ko dažkārt izmanto kvantu mehānikā. To definē šādi

ℏ = h 2 π { {displaystyle \hbar ={\frac {h}{2\pi }}}.

Kvantu mehānikā SI vienību vietā dažkārt izmanto Planka vienības. Šajā sistēmā reducētajai Planka konstantai ir vērtība 1, tātad Planka konstantes vērtība ir 2π.

Tagad Planksa konstantu var izmērīt ar ļoti augstu precizitāti. Tas ir licis BIPM apsvērt jaunu kilograma definīciju. Kilograma definīcijai vairs netiek izmantots starptautiskais prototips kilograms. Tā vietā BIPM definē Plankas konstantes precīzu vērtību. Zinātnieki izmanto šo vērtību, kā arī metra un sekundes definīcijas, lai noteiktu kilogramu.

 

Teorētiskās Planka konstantes vērtība

Planka konstanti var iegūt arī matemātiski:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6,63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{{[{q_{0}}}{[0,9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6,63\reiz 10^{-34}J\cdot s}

Šeit μ 0 {\displaystyle \mu _{0}} ir brīvās telpas caurlaidība, c {\displaystyle c} ir gaismas ātrums, q 0 {\displaystyle q_{0}} ir elektronu elektriskais lādiņš, a 0 {\displaystyle a_{0}} ir Bora rādiuss un f 1 r {\displaystyle f_{1r}} ir elektronu griešanās frekvence ūdeņraža atomā ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3,29\reiz 10^{15}rev/s)} . Ja šīs konstantu vērtības aizstāj ar teorētisko Planka konstantu, teorētiskā Planka konstantas vērtība ir precīzi vienāda ar eksperimentālo vērtību.

Saistītās lapas

• Viļņu un daļiņu dualitāte