Heizenberga nenoteiktības princips

Diagrammas

6. Šī animācija parāda vienu no svarīgākajām Visuma nenoteiktības sekām - elektronu kvantu tuneļošanu. Aplūkojiet uzmanīgi. Katru reizi, kad mazs gabaliņš izkļūst cauri barjerai.


5. Centrā esošās spraugas piekāršana ar atsperes svariem ļauj izmērīt impulsu, taču, to darot, sprauga neprognozējami pārvietojas, tāpēc informācija par katra fotona atrašanās vietu pa vidu tiek zaudēta.


4. Atspera, kas piestiprināta pie barjeras ar mazu caurumu, liek daļiņai izspiesties caur caurumu, kas izstumj barjeru, izstiepj atsperes un tādējādi mēra impulsu. Taču, tā kā atsperes piestiprinātā barjera kustas, mēs neesam tik droši par to, kur daļiņa atradās, kad tā izlidoja caur caurumu, un difrakcija arī ietekmēs tās atrašanās vietu uz detektēšanas ekrāna.


3. Sašaurinot caurumu, palielinās pārliecība par to, kur fotons atrodas vidū, bet tad tā virziens no turienes uz atklāšanas ekrānu labajā pusē kļūst attiecīgi nenoteiktāks. Fokuss kļūst neskaidrs. Paplašinot caurumu, visi fotoni nonāk detektēšanas ekrāna centrā, bet tad mums ir mazāk pārliecības par to, kur tie atradās, kad šķērsoja centrālo barjeru.


1. Fotoni, elektroni un citas subatomārās daļiņas, izšautas caur lielu caurumu, nonāk asā fokusā, bet mēs nezinām, kur tieši tās atradās ceļa vidū.


2. Sašaurinot caurumu, daļiņu ceļi ap cauruma malām tiek izliekti (difrakcija), tāpēc iegūtais staru kūlis kļūst lielāks un maigāks.

Kā cilvēki uzzināja par nenoteiktību?

Ļoti drīz pēc tam, kad Verners Heizenbergs radīja jauno kvantu fiziku, no viņa matemātikas izrietēja kaut kas negaidīts - izteiciens:

Δ x Δ p ≳ h 4 π { {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

Pozīcijas (x) kļūdas diapazons, reizināts ar impulsa (p) kļūdas diapazonu, ir aptuveni vienāds vai lielāks par Planka konstanti, kas dalīta ar 4π.

Šie simboli matemātiskā formā izsaka to, ko jūs jau esat redzējuši attēlos iepriekš. Šie simboli skaidri norāda, ka nevar būt pilnīgi pārliecināts par to, kur kaut kas atrodas un kur tas iet. Ja jums kļūst skaidrāks, kur tas atrodas jebkurā brīdī, tad jums ir mazāk pārliecības par to, kur tas iet un cik ātri. Ja jums kļūst skaidrāks priekšstats par to, kur tas iet un cik ātri, tad jums ir mazāk skaidrs, kur tas atrodas tieši tagad.

Zinātnieki jau bija uzzinājuši, kāpēc dažas vielas, kad tās tiek uzkarsētas vai citādi ierosinātas, izdala raksturīgas gaismas krāsas. Heizenbergs mēģināja izskaidrot, kāpēc katrai no šīm krāsām ir raksturīgs spilgtums. Tas nebūtu bijis pietiekami labi, ja viņš un citi zinātnieki būtu vienkārši teikuši: "Nu, tā tas vienkārši ir." Tas būtu bijis pietiekami. Viņi bija pārliecināti, ka šīm atšķirībām un faktam, ka spilgtās līnijas stipruma attiecībām katrā elementa paraugā vienmēr ir vienāds spēks, ir jābūt pamatotam iemeslam.

Viņam nebija ne jausmas, ka viņš uzdrošināsies saskarties ar apslēptu dabas noslēpumu, kad devās atklāt katram elementam raksturīgo krāsaino līniju intensitātes izskaidrojumu. Kvantu mehānikas pētījumi jau bija parādījuši, kāpēc ūdeņradim ir četras spilgtas līnijas tajā spektra daļā, ko var saskatīt cilvēks. Jādomā, ka nākamais, ko vajadzēja iemācīties, bija vienkārši aprēķināt to spilgtumu. Ūdeņradis šķita acīmredzams sākums, jo ūdeņradim ir tikai viens elektrons un tikai četras līnijas redzamajā spektra daļā. Protams, ir jābūt pamatotam iemeslam, kāpēc tās nav vienlīdz spilgtas. Neona un pārējo elementu dažādu krāsu līniju spilgtuma skaidrojums varēja pagaidīt.

 

Heizenbergs sāka strādāt pie kvantu fizikas, pielāgojot klasiskos elektrības vienādojumus, kas sākumā ir ļoti sarežģīti, tāpēc viņa 1925. gada darba matemātikai bija ļoti grūti sekot.

Viņš mēģināja atrast pareizo veidu, kā aprēķināt spilgto līniju intensitāti ūdeņraža lampas spektrā. Viņam vajadzēja atrast saistīto lielumu, ko sauca par "amplitūdu", un reizināt amplitūdu ar amplitūdu (citiem vārdiem sakot, viņam vajadzēja kvadrātēt amplitūdu), lai iegūtu vēlamo intensitāti. Viņam bija jāizdomā, kā izteikt amplitūdu tā, lai ņemtu vērā to, ka ūdeņraža lampas neizstaro visās frekvencēs un neizstaro nepārtrauktā frekvenču diapazonā tajā spektra daļā, ko cilvēki var redzēt. Heizenbergs atrada ievērojamu jaunu amplitūdas aprēķināšanas veidu.

Dīvainais vienādojums|vienādojums, ko Heizenbergs atklāja un izmantoja, lai vienu kvantu lielumu (piemēram, pozīciju) reizinātu ar citu (piemēram, impulsu), tika publicēts tā dēvētajā "Heizenberga "maģiskajā" 1925. gada jūlija rakstā".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Iepriekšminētā matemātika izskatās ļoti sarežģīta, taču matemātika, kas to veic, ir daudz sarežģītāka un ir ārkārtīgi grūti saprotama. Šeit tā ir dota tikai tāpēc, lai parādītu, kā tā izskatījās. Heizenberga darbs ir vēsturisks pagrieziena punkts. Daudzi fiziķi, kas lasīja viņa darbu, teica, ka viņi nevar nepiekrist viņa secinājumiem, bet viņi nevar saprast viņa skaidrojumu, kā viņš nonāca pie šiem secinājumiem. Sākuma vienādojumi, ko izmantoja Heizenbergs, ietvēra Furjē virknes un ietvēra daudzus koeficientus. Mēs atgriezīsimies pie iepriekš minētā vienādojuma, jo tas ir sava veida recepte matricu izrakstīšanai un reizināšanai.

Jaunajiem vienādojumiem bija jābūt tik dīvainiem un neparastiem, jo Heizenbergs aprakstīja dīvainu pasauli, kurā dažas lietas, piemēram, elektronu orbītas, lēnām ne palielinās vai samazinās. Jaunā veida izmaiņas ietver lēcienus un lielus starplaikus starp lēcieniem. Elektroni var lēkt tikai starp noteiktām orbītēm, un, mainoties orbītēm, iegūtā vai zaudētā enerģija rodas, kad tiek absorbēts pareizās enerģijas fotons vai radīts jauns pareizās enerģijas fotons. Ja ūdeņraža atomos elektroni visbiežāk lec uz leju (krīt) starp divām konkrētām orbītēm, tad šajā enerģijas līmenī tiks izstarots vairāk fotonu, un tādējādi šajā līmenī radītā gaisma būs visintensīvākā.

Bija grūti panākt, lai vienādojumi, kas veidoti nepārtrauktiem spektriem (ko redzat, kad saules gaismu izlaižat caur prizmu), atbilstu spektriem, kuros ir tikai dažas maksimālās frekvences, starp kurām nav nekā. Gandrīz viss, kas jau bija apgūts par gaismu un enerģiju, bija saistīts ar lieliem objektiem, piemēram, degošām svecēm vai saulēm, un visi šie lielie objekti rada nepārtrauktus spektrus. Lai gan ar šīm parastā izmēra lietām bija viegli veikt eksperimentus, tomēr bija nepieciešams ilgs laiks, lai noskaidrotu likumsakarības, kas tās regulē. Tagad fiziķi nodarbojās ar lietām, kas bija pārāk mazas, lai tās varētu saskatīt, lietām, kas neradīja nepārtrauktus spektrus, un centās atrast veidu, kā no jau zināmā iegūt vismaz norādes, kas palīdzētu atrast likumus šiem mazajiem un izplūdušajiem gaismas avotiem.

Sākotnējie vienādojumi attiecās uz sava veida vibrējošu ķermeni, kas radītu vilni, līdzīgi kā ērģeļu niedres rada skaņas vilni ar raksturīgu frekvenci. Tātad bija kustība uz priekšu un atpakaļ (līdzīgi kā vibrējot niedrei), un tika emitēts vilnis, ko varēja attēlot kā sinusoidālu vilni. Liela daļa no tā, kas jau agrāk tika noskaidrots par fiziku atomu līmenī, bija saistīta ar elektronu kustību ap kodoliem. Kad masa pārvietojas pa orbītu, kad tā rotē ap kādu centru, tai ir tā saucamais "leņķiskais moments". Leņķiskais moments ir veids, kā kaut kas tāds kā karuselis turpina griezties pēc tam, kad cilvēki ir pārtraukuši to stumt. Matemātika, ko izmanto fāžu aprēķinos un leņķiskā momenta aprēķinos, ir sarežģīta. Turklāt Haizenbergs savā 1925. gada rakstā nav parādījis visus savus aprēķinus, tāpēc pat labiem matemātiķiem var rasties grūtības aizpildīt to, ko viņš nav pateicis.

Lai gan daudzi fiziķi apgalvoja, ka viņi nespēja izprast dažādus matemātikas soļus Heizenberga izšķirošajā darbā, vienā nesen publicētā rakstā, kurā mēģināts izskaidrot, kā Heizenbergs ieguva savu rezultātu, ir divdesmit matemātikas pilnas lappuses. Pat šis raksts nav viegli saprotams. Matemātika sākās ar patiešām sarežģītām lietām, un galu galā radās kaut kas salīdzinoši vienkāršs, kas parādīts šī raksta augšpusē. Vienkāršāka rezultāta iegūšana nebija viegla, un mēs nemēģināsim parādīt procesu, kā no novecojušas Visuma ainas nonākt līdz jaunajai kvantu fizikai. Mums ir nepieciešams tikai pietiekami daudz detaļu, lai parādītu, ka gandrīz tiklīdz Heizenbergs veica savu izrāvienu, atklājās tāda Visuma darbības daļa, kādu neviens iepriekš nebija redzējis.

Heizenbergs droši vien bija ļoti satraukts, bet arī ļoti noguris, kad vēlu vakarā viņš beidzot izdarīja savu atklājumu un sāka pierādīt sev, ka tas darbosies. Gandrīz uzreiz viņš pamanīja kaut ko dīvainu, kaut ko, ko viņš uzskatīja par kaitinošu mazu problēmu, ko viņš varētu kaut kā novērst. Taču izrādījās, ka šī nelielā neērtība bija liels atklājums.

Heizenbergs bija strādājis pie amplitūdas reizināšanas ar amplitūdām, un tagad Heizenbergam bija labs veids, kā izteikt amplitūdu, izmantojot savu jauno vienādojumu. Protams, viņš domāja par reizināšanu un par to, kā viņš reizinātu lietas, kas bija dotas ar sarežģītiem vienādojumiem.

Heizenbergs saprata, ka līdztekus amplitūdas reizināšanai ar kvadrātu viņš galu galā vēlēsies reizināt pozīciju ar impulsu vai enerģiju ar laiku, un šķita, ka būs kāda atšķirība, ja viņš šajos jaunajos gadījumos apgriezīs kārtību. Heizenbergs nedomāja, ka būtu svarīgi, vai reizināt pozīciju ar impulsu vai reizināt impulsu ar pozīciju. Ja tie būtu tikai vienkārši skaitļi, problēmu nebūtu. Taču tie abi bija sarežģīti vienādojumi, un izrādījās, ka tas, kā iegūt skaitļus, ko ievietot vienādojumos, ir atšķirīgi atkarībā no tā, no kuras puses sākāt. Dabā vajadzēja izmērīt pozīciju un tad izmērīt impulsu, vai arī vajadzēja izmērīt impulsu un tad izmērīt pozīciju, un matemātikā valdīja tā pati vispārējā situācija. (Ja vēlaties uzzināt sīkāk, skatiet angļu Vikipēdijas rakstu Heizenberga ievads matricas mehānikā!). Nelielās, bet kaitinošās atšķirības starp rezultātiem saglabāsies, lai arī cik ļoti Heizenbergs vēlējās, lai tās izzustu.

Tolaik Heizenbergs nespēja atbrīvoties no šīs mazās problēmas, bet viņš bija noguris, tāpēc nodeva savu darbu tiešajam priekšniekam Maksam Bornam un devās atvaļinājumā.

Makss Borns bija izcils matemātiķis, kurš drīz vien saprata, ka Heizenberga dotais vienādojums ir sava veida recepte matricas rakstīšanai. Dr. Borns bija viens no nedaudzajiem cilvēkiem, kas tajā laikā interesējās par šo dīvaino matemātikas veidu, par kuru lielākā daļa cilvēku uzskatīja, ka tas nav īpaši noderīgs. Viņš zināja, ka matricas var reizināt, tāpēc visu aprēķinu veikšanu vienas fizikas problēmas uzskaitei varēja veikt, reizinot vienu matricu ar citu. Vienkārši spēja sarežģītu procedūru ietērpt standarta un pieņemamā formā atvieglotu darbu. Tas varētu arī atvieglot tās pieņemšanu citiem cilvēkiem.

Borns bija tik labs matemātiķis, ka viņš gandrīz uzreiz saprata, ka, mainot abu matricu reizināšanas kārtību, tiks iegūts atšķirīgs rezultāts, un rezultāti atšķirsies par nelielu summu. Šī summa būtu h/2πi. Ikdienā šī atšķirība būtu tik maza, ka mēs to pat nevarētu pamanīt.

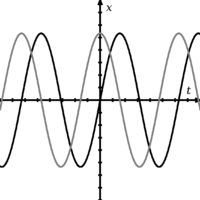
Divi viļņi, kas nav savstarpēji fāzēti.


Neona spektrs


Pilns saules vizuālais spektrs. Nav nekādu nepilnību. Šajā diagrammā parādīta intensitāte dažādās frekvencēs.


Kad noteiktas molekulas tiek uzbudinātas, tās izdala raksturīgu krāsu.


Ūdeņraža spektrs

Par formālu nenoteiktības teoriju

Pagāja vairāki gadi, bet Heizenbergam izdevās pierādīt nenoteiktības principu, kas nosaka, ka Δx × Δp = h/2, kas ir skaitlis, kurš izriet no sākotnējiem vienādojumiem, bet neietver π un i, kas ir saistīti ar fāžu izmaiņām. Heizenbergs paskaidroja, ka savu nenoteiktības principu viņš atvasināja no šī agrākā rezultāta, kad 1927. gadā uzrakstīja darbu, kurā iepazīstināja ar šo teoriju.

Konstante h, ko sauc par Planka konstanti, ir noslēpumains skaitlis, kas bieži sastopams, tāpēc mums ir jāsaprot, kas ir šis niecīgais skaitlis. Skaitliski tas parasti ir 6,62607×10^-34 J s (džoulsekundes). Tātad tas ir lielums, kas ietver enerģiju un laiku.

To atklāja, kad Planks saprata, ka perfekta radiatora (tā saucamā melnā ķermeņa radiatora) enerģija tiek izstarota noteikta lieluma vienībās, ko sauc par "kvantiem" (šī vārda vienskaitlis ir "kvants"). Izstarotā enerģija tiek izstarota fotonu veidā, un fotona frekvence ir proporcionāla tā "triecienam". Dažādas redzamās gaismas frekvences mēs izjūtam kā dažādas krāsas. Violetajā spektra galā katram fotonam ir relatīvi liels enerģijas daudzums; sarkanajā spektra galā katram fotonam ir relatīvi mazs enerģijas daudzums. Fotona enerģijas daudzumu var aprēķināt pēc vienādojuma E = hν (enerģija ir vienāda ar Planka konstantes reizinājumu ar "nu" jeb frekvenci).

Heizenberga nenoteiktības princips Δx × Δp ≥ h saka mums, ka ikreiz, kad mēs mēģinām precīzi noteikt dažus skaitļu pārus, mēs varam tikai tik tuvu, un ka, ja mēs mēģinām precizēt vienu no tiem, t. i., ja mēs mēģinām padarīt Δx mazāku, lai mums būtu labāks priekšstats par kaut kā pozīciju, tad mums būs jāsaņem atpakaļ lielāks skaitlis par otru pāra skaitli, un ka abu skaitļu novirze ir cieši saistīta ar h.

Cits fizikālo lielumu pāris atbilst nenoteiktības sakarībai: ΔE × Δt ≥ h, un šis pāris cita starpā norāda, ka, ja mēs skatāmies starpzvaigžņu telpā, kādā vietā, kur mēs vispār neko negaidītu atrast, un mēs samazinām Δt arvien tuvāk un tuvāk 0, tad, lai saglabātu vienādojumā norādīto līdzsvaru, ΔE ir jākļūst arvien lielākam - un pēkšņi kaut kas ar impulsu var parādīties tikai uz šo īso laika periodu.

Kā izskaidrot šo nenoteiktību (nenoteiktības trūkumu)? Kas notiek Visumā? Bieži tiek teikts, ka jauna teorija, kas ir veiksmīga, var sniegt jaunu informāciju par pētāmajām parādībām. Heizenbergs izveidoja matemātisku modeli, kas paredzēja pareizu intensitāti ūdeņraža spilgtās līnijas spektram, taču, negatavojoties to darīt, viņš atklāja, ka daži fizikālo lielumu pāri atklāj negaidītu nenoteiktību. Līdz tam brīdim nevienam nebija ne jausmas, ka mērījumus nevar mūžīgi padarīt arvien precīzākus un precīzākus. Fakts, ka tos nevar padarīt noteiktākus, precīzākus, bija satriecošs atklājums. Daudzi cilvēki nebija gatavi to pieņemt.

Bors un viņa kolēģi apgalvoja, ka fotoniem, elektroniem u.c. nav ne pozīcijas, ne impulsa, kamēr tie netiek izmērīti. Šī teorētiskā nostāja izauga no nenoteiktības atklājuma, un tā nebija tikai kāda personiska izvēle, kam ticēt. Bors teica, ka mēs neko nezinām par kaut ko tādu kā fotons vai elektrons, kamēr mēs to nepamanām. Lai novērotu tik mazu lietu, mums ar to ir kaut kā jāsadarbojas. Ikdienā ir iespējams darīt kaut ko tādu, piemēram, staigāt līdzās automobilim, atzīmējot laikus, kad tas šķērso punktus uz ietves uzzīmētā režģī. Iespējams, automobiļa svars pats nospiedīs mazas sviras bruģī, kas ieslēgs pie katras no tām piestiprinātus pulksteņus un reģistrēs automobiļa svaru. Galu galā mums būtu skaidrs ieraksts par to, kur automašīna atradās dažādos laikos, kā arī mēs varētu aprēķināt tās kustības virzienu un svaru. Tad mēs varētu zināt, jebkurā laikā uz pulksteņa, gan tā atrašanās vietu, gan tā kustības momentu (ātrums reizināts ar masu). Mēs pat iedomāties nevarētu, ka spēks, kas vajadzīgs, lai pārvietotu mazās sviras, kaut kā ietekmētu automašīnas kustību. Mēs arī neiedomātos, ka automobilim nav atrašanās vietas vai trajektorijas starp punktiem uz bruģa, kur ir sviras, vai ka automobilis šajos laikos eksistē sava veida trīsdimensiju miglā un nostājas tikai tad, kad tas nospiež kādu sviru. Mums pazīstamā pasaule neatklāj šos dīvainos mijiedarbības veidus.

Lai noteiktu kuģa atrašanās vietu jūrā tumšākajā naktī, mēs varētu izmantot prožektoru, un šī gaisma netraucētu kuģa atrašanās vietu vai kustības virzienu, bet, lai noteiktu elektrona atrašanās vietu ar gaismu, būtu nepieciešams to notriekt ar vienu vai vairākiem fotoniem, no kuriem katram ir pietiekams impulss, lai traucētu elektrona atrašanās vietu un trajektoriju. Lai elektronu atrastu ar citiem līdzekļiem, tas būtu jātur kādā fiziskā ierobežojumā, kas arī pārtrauktu tā kustību uz priekšu.

Lai noteiktu fotona atrašanās vietu, labākais, ko var izdarīt, nepārtraucot tā kustību uz priekšu, ir likt tam iziet cauri apļveida caurumam barjerā. Ja ir zināms laiks, kad fotons tika izstarots (piemēram, ar lāzeru), un laiks, kad fotons nonāk uz detektēšanas ekrāna, piemēram, digitālās kameras, tad ir iespējams aprēķināt laiku, kas nepieciešams, lai veiktu šo attālumu, un laiku, kad fotons izgāja caur caurumu. Tomēr, lai caur to varētu izlaist fotonu, apļveida cauruma diametram jābūt lielākam par fotona izmēru. Jo mazāks ir apļveida caurums, jo tuvāk mēs zinām precīzu fotona atrašanās vietu, kad tas caur to iet. Tomēr mēs nekad nevaram zināt, vai fotons tajā brīdī ir novirzīts no centra. Ja caurums ir tieši tāda paša izmēra kā fotons, tas cauri neizies. Samazinoties cauruma diametram, fotona impulss jeb virziens, tam izejot no cauruma, arvien vairāk un vairāk mainās.

Nilss Bors un viņa kolēģi apgalvoja, ka mēs nonākam lielās nepatikšanās, ja pieņemam par patiesām lietas, kas ir pārāk mazas, lai tās redzētu pat ar mikroskopu, jebko, par ko mums ir pierādījumi tikai ikdienas dzīves mērogā. Ikdienas dzīvē lietām vienmēr ir noteikta atrašanās vieta. Atomu mērogā mums nav pierādījumu, kas pamatotu šādu secinājumu. Ikdienas dzīvē lietām ir noteikts laiks, kurā tās notiek. Atomu mērogā mums nav pierādījumu, kas pamatotu šādu secinājumu. Ikdienā, ja kāds novēro rūpnīcu no pirmās dienas nakts maiņas līdz otrās dienas maiņai un redz, kā gatavs automobilis tiek izvests uz nosūtīšanas piestātni, nebūtu jēgas apgalvot, ka nav iespējams noteikt, vai tas piegādāts nakts vai dienas maiņas laikā. Bet atomu mērogā mēs varam parādīt gadījumus, kad mums ir jāuzskata, ka viens fotons ir radies divos laikos. (Ja tas nav pietiekami slikti, mēs varam parādīt arī gadījumus, kad viens fotons ir radīts no diviem blakus esošiem lāzeriem.)

Daļa no grūtībām noskaidrot, kas notiek atomu mērogā, ir saistītas ar to, ka mēs vēlamies zināt gan to, kur kaut kas atrodas, gan to, kāda ir tā trajektorija, un zināt abas šīs lietas vienlaicīgi, bet mēs nevaram izmērīt gan pozīciju, gan trajektoriju vienlaicīgi. Mēs vai nu vienā reizē izmērām fotona vai elektrona impulsu un pēc tam bez liekas kavēšanās izmērām tā pozīciju, vai arī mēs apmaināmies un vispirms izmērām pozīciju, bet pēc tam impulsu. Problēma ir tā, ka, liekot pirmajam mērījumam iegūt diezgan noteiktu formu (kaut kādā veidā to saspiežot), mēs palielinām nenoteiktību, kas saistīta ar nākamo mērījumu. Ja mūsu sākotnējie mērījumi būtu tik neapstrādāti, ka katrā no tiem būtu ieviesta liela kļūda, tad mēs varētu uzlabot situāciju, izmantojot vieglāku pieskārienu, lai veiktu katru no tiem, bet mēs nekad nevarētu pārsniegt noteiktu precizitātes robežu.

No ikdienas dzīves mēs zinām, ka, mēģinot kaut ko nosvērt uz vannas istabas svariem, kas novietoti uz veļas mazgājamās mašīnas griešanās ciklā, rezultāti būs neprecīzi, jo svaru adata stipri svārstīsies. Mēs varam izslēgt veļas mašīnu. Bet, lai veiktu ļoti precīzus mērījumus, mēs redzam, ka kaimiņos braucošās kravas automašīnas liek adatai trīcēt, tāpēc mēs varam novietot svarus uz kaut kā, lai tos izolētu no ārējiem traucējumiem. Mēs uzskatām, ka varam pietiekami novērst vibrācijas, lai iegūtu tik precīzus rezultātus, cik vēlamies. Mēs nekad neņemam vērā, ka skala pati vibrē vai ka tai piemīt nenoteikts impulss.

Argumentējot atpakaļ no nenoteiktības principa, šķiet, ka patiesībā nevienai atoma mēroga lietai nav noteiktas pozīcijas un noteikta impulsa un ka eksperimentētāji var tikai piespiest lietas noteikt noteiktību nenoteiktības principa noteiktajās robežās. Bors un viņa kolēģi tikai apgalvoja, ka mēs neko nevaram uzzināt, neveicot mērījumus, un, veicot mērījumus, mēs varam virzīt lietas noteiktākas pozīcijas vai noteiktāka impulsa virzienā, bet mēs nevaram iegūt absolūtu noteiktību vai noteiktību, kādu mēs vēlētos. Taču citi uztvēra šo iespēju nopietni un apgalvoja, ka, ja matemātikai ir taisnība, tad ultra mazo pasaulē nevar būt noteiktības vai noteiktības. Zinātnes būtība ir tāda, ka matemātika ir tikai realitātes modelis, un nav garantijas, ka tas ir pareizs modelis.

Matemātika un matemātikā prognozēto lietu praktiskās sekas ir tik uzticamas, ka tām ir ļoti grūti nepiekrist, taču tas, ko matemātika saka par reālo pasauli, ir radījis vairākas atšķirīgas idejas. Starp zinātniekiem, kas strādāja kopā ar Nils Boru Kopenhāgenā, nenoteiktības princips tika uzskatīts par to, ka elementārā līmenī fiziskais visums nepastāv deterministiskā formā. Drīzāk tas ir varbūtību vai potenciālu kopums.

Pretstatā Kopenhāgenas grupas ap matemātiku savītajam stāstam ir arī citi stāsti, piemēram, "vairāku visumu interpretācija", kas saka, ka katru reizi, kad saskaņā ar kvantu teoriju ir vairāki iespējamie iznākumi, katrs iznākums notiek savā jaunā visumā. Einšteins apgalvoja, ka nav vairāku iespējamo iznākumu, tāpēc ir tikai viens visums, un tas ir determinēts, jeb, kā viņš teica, "Dievs nespēlē kauliņus".

Ja h būtu mazākais iespējamais enerģijas daudzums, tad pamatvienādojums, kas parāda dažādu frekvenču fotonu enerģiju, nebūtu līdzsvarots. Tas būtu nepareizs.

Iebildumi pret nenoteiktības principu

Alberts Einšteins saskatīja, ka jaunā kvantu mehānika nozīmē to, ka laikā pirms mērījumu veikšanas nav pozīcijas un impulsa, un viņš stingri iebilda pret to. Viņš bija stingri pārliecināts, ka lietām pirms mērījumu veikšanas bija noteiktas pozīcijas un noteikti momenti un ka fakts, ka, izmērot vienu no pāra lietām un traucējot iespēju precīzi izmērīt otru, neapgalvo, ka pirms mērījumu veikšanas kāda no tām nav bijusi. Viņš un divi viņa kolēģi uzrakstīja darbu, kas kļuvis pazīstams kā "EPR dokuments". Šajā rakstā tika apgalvots, ka ir jābūt īpašībām, kas nosaka pozīciju un impulsu, un, ja mēs tās varētu redzēt vai ja mēs varētu iegūt informāciju par tām, tad mēs varētu matemātiski zināt un prognozēt pozīciju un impulsu. Ilgu laiku cilvēki uzskatīja, ka nav iespējams pierādīt vai atspēkot to, kas Einšteinam bija ticības princips. Šis strīds bija ļoti produktīvs, jo tas noveda pie visiem mūsdienu sasniegumiem iepinējumā.

Matemātiski ir pierādīts, ka Einšteins ir kļūdījies. 1964. gadā Džons Stjuarts Bells (John Stewart Bell) izstrādāja matemātisku metodi, lai nošķirtu divu daļiņu uzvedību, kurām ir determinēti stāvokļi, kas ir tikai nezināmi diviem indivīdiem, kuri tos pēta, un divu daļiņu, kurām ir savijušies stāvokļi, kas ir nenoteikti vai neskaidri, līdz tie tiek izmērīti. Viņa metode rāda, ka varbūtības iegūt noteiktus rezultātus ir atšķirīgas, ja tiek ievēroti divi dažādi pieņēmumi. Viņa darbu sauc par Bella teorēmu vai Bella nevienādību. Eksperimenti ir pierādījuši, ka daba uzvedas tā, kā to apraksta Bells.

Vēl viens ceļš uz nenoteiktību

Sākotnējās diskusijas par Heizenberga nenoteiktības principu bija atkarīgas no modeļa, kurā netika ņemts vērā, ka tādām matērijas daļiņām kā elektroniem, protoniem utt. ir viļņa garums. 1926. gadā Luijs de Brolijs pierādīja, ka visām lietām, ne tikai fotoniem, ir sava frekvence. Tāpat kā fotoniem, arī lietām piemīt viļņu un daļiņu daba. Ja mēs mēģinātu padarīt tādas lietas kā protonu vilni šaurāku un garāku, tas padarītu tās stāvokli skaidrāku, bet tad impulss kļūtu mazāk noteikts. Ja mēs mēģinātu viļņa apraksta impulsa daļu padarīt skaidrāku, t. i., liktu tam palikt šaurākā vērtību diapazonā, tad viļņa maksimums izplestos un tā pozīcija kļūtu mazāk noteikta.

Kvantu mehānikā vilnis, kas ir daļa no fotona apraksta, nav tas pats, kas vilnis okeāna virspusē vai saspiesta gaisa un retināta gaisa apgabali, kas veido skaņas viļņus. Tā vietā šiem viļņiem ir maksimumi jeb augstas amplitūdas apgabali, kas ir saistīti ar varbūtību kaut ko atrast šajā telpas un laika punktā. Precīzāk, tieši amplitūdas kvadrāts ir tas, kas nosaka kādas parādības parādīšanās varbūtību.

Fotonam piemērojamais vilnis varētu būt tīrs sinusoidāls vilnis. Tādā gadījumā katra maksimuma vērtības kvadrāts dotu fotona novērošanas varbūtību šajā punktā. Tā kā sinusoidālo viļņu amplitūdas visur ir vienādas, varbūtība atrast fotonu katrā no tiem būtu vienāda. Tātad, praktiski runājot, zinot viļņu kādam no šiem fotoniem, nebūtu iespējams noteikt, kur to meklēt. No otras puses, fotona impulss ir matemātiski saistīts ar tā viļņa amplitūdu. Tā kā šajā gadījumā mums ir tīrs sinusoidāls vilnis, katra viļņa cikla amplitūda ir vienāda, un tāpēc ar šo vilni ir saistīta tikai viena impulsa vērtība. Mēs nezinātu, kur fotons trāpīs, bet mēs precīzi zinātu, cik spēcīgi tas trāpīs.

Gaismas staru kūļos, kas fokusējas uz kādu punktu uz detektēšanas ekrāna, ar fotoniem saistītie viļņi nav tīri sinusoidāli viļņi. Tā vietā tie ir viļņi ar augstu amplitūdu vienā punktā un daudz zemāku amplitūdu abpus šim augstākajam maksimumam. Matemātiski šādu vilni ir iespējams analizēt vairākos dažādos sinusoidālos viļņos ar dažādu viļņu garumu. Nedaudz vieglāk ir iztēloties šī procesa pretējo versiju, aplūkojot sākotnējo vienas frekvences sinusoidālo vilni, kuram pievieno otru sinusoidālo vilni ar citu viļņa garumu, tad trešo, ceturto utt. Rezultātā veidojas sarežģīts vilnis ar vienu augstu maksimumu, kas satur lielu skaitu viļņu ar dažādiem viļņu garumiem un līdz ar to ar dažādiem momentiem. Tādā gadījumā varbūtība, ka fotons parādīsies noteiktā punktā, ir ārkārtīgi liela, bet tā sniegtais impulss var izrādīties saistīts ar jebkura no viļņa komponentiem viļņa garumu. Citiem vārdiem sakot, p = ħ/λ vērtība vairs nav vienreizēja vērtība, jo jāņem vērā visu salikto "viļņu ar dažādu viļņu garumu" garumi.

Simulācijā parādīts, kā matemātiski modelēt daļiņas atrašanās vietas saasināšanos: Uz sākotnējā sinusoidālā viļņa uzliek daudzas dažādas viļņu formas. Centrā veidosies arvien augstāks un augstāks maksimums, bet pārējo maksimumu skaits palielināsies, bet augstums samazināsies, jo tie savstarpēji interferēs. Tādējādi superpozīcijā galu galā ir daudz dažādu viļņu, katrs ar atšķirīgu viļņa garumu un (pēc p = ħ/λ) atšķirīgu impulsu, bet tikai viens ļoti augsts maksimums, kas kļūst arvien augstāks un šaurāks un dod mums kaut ko arvien tuvāku un tuvāku noteiktai pozīcijai.

Lai impulsu padarītu arvien noteiktāku, mums būtu jāatņem arvien vairāk un vairāk uzlikto sinusoidālo viļņu, līdz mums paliktu tikai vienkāršs sinusoidālais vilnis. Šādi rīkojoties, mēs pakāpeniski samazinātu centrālā maksimuma augstumu un pakāpeniski palielinātu to konkurējošo vietu augstumu, kurās varētu atrast daļiņu.

Tāpēc, kad mēs sākam ar subatomāro daļiņu viļņu attēlu, mēs parasti vienmēr saskaramies ar gadījumiem ar relatīvi augstiem centrālajiem maksimumiem un relatīvi daudziem komponentu viļņu garumiem. Šādos apstākļos nekad netiks prognozēta precīza pozīcija vai precīzs impulss. Ja matemātiskais modelis precīzi ataino reālo pasauli, tad nevienam fotonam vai citai subatomārajai daļiņai nav ne precīzas pozīcijas, ne noteikta impulsa. Mērot šādu daļiņu, mēs varam izvēlēties metodi, kas vēl vairāk saspiež maksimumu un padara to šaurāku, vai arī varam izvēlēties metodi, kas pazemina maksimumu un izlīdzina viļņu garumu sastāvdaļas. Atkarībā no tā, ko un kā mēs mēra, mēs varam padarīt mūsu atrašanās vietu precīzāku vai sašaurināt momenta diapazonu. Mēs varam rūpēties, plānojot eksperimentu, lai izvairītos no dažādiem aparāta izjokošanas veidiem, bet mēs nevaram atbrīvoties no tā, ka sākumā nebija nekā pilnīgi noteikta.

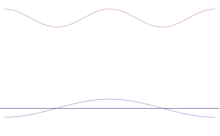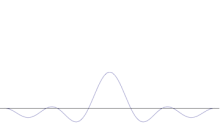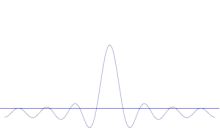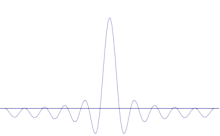
Vairāku plakano viļņu superpozīcija. Viļņu pakete kļūst aizvien lokalizētāka, pievienojot daudzus viļņus. Furjē transformācija ir matemātiska operācija, kas viļņu paketi sadala atsevišķos plakanos viļņos. Ņemiet vērā, ka šeit attēlotie viļņi ir reāli tikai ilustrācijas nolūkos, bet kvantu mehānikā viļņu funkcija parasti ir kompleksa.

Kultūras ietekme

Haizenberga nenoteiktības principa nozīmīgākā ietekme ir bijusi uz argumentiem par gribas brīvību. Saskaņā ar klasiskās fizikas teorijām ir iespējams apgalvot, ka cēloņu un seku likumi ir neizbēgami un ka, ja reiz Visums ir sācies noteiktā veidā, tad no šī sākotnējā stāvokļa var aprēķināt visu vielu un enerģijas mijiedarbību, kas notiks nākotnē. Tā kā viss ir absolūts rezultāts tam, kas bija pirms tam, viņi apgalvoja, ka ikviens cilvēka lēmums un katra situācija, kurā viņš nonāk, ir iepriekš noteikta jau kopš laika sākuma. Tādējādi mums nav izvēles, ko darīt.

Cilvēki, kas tic gribas brīvībai, apgalvo, ka kvantu mehānikas likumi neparedz, kas notiks, bet tikai to, kas ir vairāk un kas mazāk ticams. Tāpēc katra rīcība ir nejaušas "monētas mešanas" rezultāts, un nevienu lēmumu nevar izsekot kādam nepieciešamu priekšnosacījumu kopumam.

Izteicieni "kvantu lēciens" un "kvantu lēciens" ir kļuvuši par ierastu veidu, kā runāt par lietām. Parasti cilvēki vēlas kaut ko aprakstīt kā tādu, kas saistīts ar milzīgām pārmaiņām, kuras notiek īsā laika posmā. Patiesībā šis termins attiecas uz to, kā elektrons uzvedas atomā, kad tas absorbē no ārpuses ienākošu fotonu un tādējādi pārlec no vienas orbītas ap atoma kodolu uz augstāku orbītu, vai arī kad tas izstaro fotonu un tādējādi nokrīt no augstākas orbītas uz zemāku orbītu. Neils Bors un viņa kolēģi uzskatīja, ka elektrons nepārvietojas starp orbitām, bet gan pazūd no vienas orbītas un uzreiz parādās citā orbītā. Tātad kvantu lēciens patiesībā nav nekādas satricinošas pārmaiņas, bet gan pēkšņa neliela pāreja no vienas jomas uz citu.

Ja cilvēks mēra kādu procesu subatomārā mērogā un izpaužas nenoteiktības princips, tad var teikt, ka cilvēka darbība ir ietekmējusi mērāmo lietu. Veicot mērījumu, kura mērķis ir iegūt precīzu norādi par daļiņas atrašanās vietu, neizbēgami tiks ietekmēts tās impulss, un neatkarīgi no tā, kas tiek darīts, lai pēc iespējas ātrāk pēc daļiņas atrašanās vietas mērīšanas izmērītu šo impulsu, nevar nemainīties varbūtība, kāds impulss tiks atklāts. Tādējādi nenoteiktības princips var izskaidrot dažus pētnieku radīto traucējumu veidus, kas ietekmē eksperimenta vai novērojuma rezultātus. Tomēr ne visi novērotāja efekti ir saistīti ar kvantu efektiem vai nenoteiktības principu. Pārējie ir "novērotāja efekti", bet ne kvantu nenoteiktības efekti.

Novērotāja efekts ietver visdažādākās lietas, kas darbojas mūsu parastajā cilvēcisko notikumu mērogā. Ja antropologs cenšas gūt skaidru priekšstatu par dzīvi primitīvā sabiedrībā, bet viņa klātbūtne satrauc kopienu, kuru viņš apmeklē, tad novērojumi var būt ļoti maldinoši. Tomēr neviena no attiecīgajām mijiedarbībām nenotiek tādā līmenī, ko apraksta kvantu mehānika vai nenoteiktības princips.

Dažkārt vārds "kvantu" tiek izmantots reklāmas nolūkos, lai norādītu uz kaut ko jaunu un jaudīgu. Piemēram, mazo benzīna dzinēju ražotājs Briggs and Stratton piedāvā četru cilindru mazas jaudas dzinēju līniju benzīna pļaujmašīnām un līdzīgiem dārza darbarīkiem, ko sauc par "Quantum".

Vairāk lasīšanas

• Ievads kvantu teorijā, 115. lpp. un 158. lpp.

J.P. McEvoy un Oscar Zarate