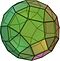
Arhimēda cietvielas: definīcija, īpašības un piemēri
Arhimēda cietvielas: skaidra definīcija, īpašības un ilustrēti piemēri — uzzini vēsturi, 13/15 figūru variācijas un to ģeometrijas pielietojumus.
Arhimēda cietviela ģeometrijā ir konveksa, izliekta daudzstūra forma, kas sastāv no regulāriem daudzstūriem un kurai visos virsotņu punktos seju izkārtojums ir vienāds. Precīzāk, arhimēda cietvielām ir šādas pazīmes:
- Katra seja ir veidota no regulāra daudzstūra (piemēram, regulāras trijstūra, četrstūra, piecstūra utt.).
- Virsotņu translatīvums (vienādība): ap katru virsotni seju izkārtojums (rinda un secība) ir tāds pats — visi virsotņi "izskatās vienādi".
- Forma ir konveksa (nav iekšējo ieliekumu) un tā nav ne platoniska cieta viela, ne parasta prizma, ne antiprisma.
- Lai konstrukcijā būtu patiesa arhimēda cietviela, parasti nepieciešami vismaz divi dažādi daudzstūru tipi (piem., trijstūri un sešstūri).
Atkarībā no tā, vai divas ķīmiski (geometriski) spoguļattēla versijas tiek uzskatītas par vienādām, tiek minēts 13 vai 15 šādu figūru kopums. Standarta klasifikācijā parasti ir 13 konveksi Arhimēda cietvielas; papildus tam divas no tām — snub-veida figūras — pastāv divos nemetālos (labās un kreisās) enantiomorfos variantos, kuri nav savstarpēji kongruenti, ja pieļauj tikai rotācijas.
Arhimēda cietvielas ir nosauktas pēc sengrieķu matemātiķa Arhimēda, kurš, iespējams, 3. gadsimtā pirms mūsu ēras aprakstījis šādas formas. Sākotnējie viņa raksti ir saglabājušies netieši; 4. gadsimtā tos daļēji apkopoja Papps no Aleksandrijas. Renesanses laikā mākslinieki un matemātiķi atjaunoja interesi par tīrām ģeometriskajām formām, un ap 17. gadsimtu — piemēram, Johannes Keplers darbos — meklējumi un klasifikācija tika papildināta.
Arhimēda cietvielas bieži veido pēc vienkāršām operācijām, piemēram, nogriešanas (truncation), rektifikācijas (rectification), paplašināšanas (cantellation) un snub-operācijas no Platoniskajām figūrām vai to kombinācijām. Katrā no šīm operācijām saglabājas seju regularitāte un virsotņu vienādība.
Katram Arhimēda cietvielas ir savs duālais daudzstūris, kas pieder pie tā saucamajām Catalan cietvielām (dualās figūras, kurās ir vienādas sejas, bet atšķirīga virsotņu simetrija). Praktiskā pielietojumā arhimēda formas parādās arhitektūrā, mēbeļu dizainā, ķīmijā (piem., fulerēni, kur struktūra atgādina nogrieztu iksosaedru) un viroloģijā (vīrusu kapsīdu simetrija).
Tipiski piemēri un labi pazīstamas Arhimēda cietvielas (angļu nosaukumi iekavās) ir:
- nogrieztais tetrahēdrs (truncated tetrahedron)
- kuboctaedrs (cuboctahedron)
- nogrieztais kubs (truncated cube)
- nogrieztais oktaedrs (truncated octahedron)
- rombikuboctaedrs (rhombicuboctahedron)
- nogrieztais kuboktaedrs / lielais rhombicuboctahedron (truncated cuboctahedron)
- snub kubs (snub cube) — chirāla, divas enantiomorfās versijas
- iksododekaedrs (icosidodecahedron)
- nogrieztais dodekaedrs (truncated dodecahedron)
- nogrieztais iksosaedrs (truncated icosahedron) — labi pazīstams kā "futbola bumba" / C60 fulerēna forma
- rombikosi dodekaedrs (rhombicosidodecahedron)
- nogrieztais iksododekaedrs (truncated icosidodecahedron)
- snub dodekaedrs (snub dodecahedron) — chirāla, divas enantiomorfās versijas
Matemātiskās īpašības: visām konveksām arhimēda cietvielām der Ūlera formula V − E + F = 2 (kur V ir virsotņu skaits, E malas, F sejas), un katrai figūrai var aprēķināt malu garumus, seju formas un iekšējos leņķus, ja zināms malas garums un seju tipu kombinācija.
Kopsavilkumā: Arhimēda cietviela ir simetriska, konveksa daudzstūra forma, kuras sejas ir regulāri daudzstūri, virsotnes ir savstarpēji līdzīgas, un kuru veidošanai nepieciešami vismaz divu veidu daudzstūri. Klasiskā kopā ir 13 šādu formu; ja iekļauj abās enantiomorfās versijas atsevišķi, tad to ir 15.
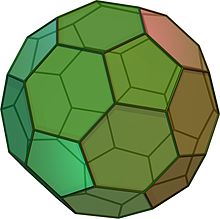
Saīsinātais ikosaedrs izskatās kā futbola bumba. Tas sastāv no 12 vienādmalu piecstūriem un 20 regulāriem sešstūriem. Tam ir 60 virsotnes un 90 malas. Tas ir Arhimēda cietviela.
Īpašības
- Arhimēda ķermeņi ir veidoti no regulāriem daudzstūriem, tāpēc visām malām ir vienāds garums.
- Visus Arhimēda cietos ķermeņus var izveidot no Platona cietajiem ķermeņiem, "sagriežot malas" Platona cietajam ķermeņam.
- Daudzstūru veids, kas satiekas stūrī ("virsotne"), raksturo gan arhimēda, gan platona cietvielu.
Saistība ar Platona cietvielām
Platona cietos ķermeņus var pārvērst par Arhimēda cietajiem ķermeņiem, ievērojot virkni to uzbūves noteikumu.
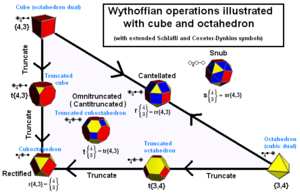
Arhimēdu cietvielas var konstruēt kā ģeneratora pozīcijas kaleidoskopā.
Arhimēda cieto ķermeņu saraksts
Turpmāk ir uzskaitītas visas Arhimēda cietvielas.
| Attēls | Nosaukums | Sejas | Tips | Malas | Virsotnes |
|
| Saīsināts tetraedrs | 8 | 4 trīsstūri 4 sešstūri | 18 | 12 |
|
| 14 | 8 trīsstūri 6 laukumi | 24 | 12 | |
|
| Saīsināts kubs | 14 | 8 trīsstūri 6 astoņstūri | 36 | 24 |
|
| Saīsināts astoņstūris | 14 | 6 laukumi 8 sešstūri | 36 | 24 |
|
| Rombikuboktaedrs | 26 | 8 trīsstūri 18 laukumi | 48 | 24 |
|
| Saīsināts kuboktaedrs | 26 | 12 laukumi 8 sešstūri 6 astoņstūri | 72 | 48 |
|
| Snub cube (2 spoguļattēlu versijas) | 38 | 32 trīsstūri 6 laukumi | 60 | 24 |
|
| Ikozidodekaedrs | 32 | 20 trīsstūri 12 piecstūri | 60 | 30 |
|
| Saīsināts dodekaedrs | 32 | 20 trīsstūri 12 dekagoni | 90 | 60 |
|
| Saīsināts ikozaedrs | 32 | 12 piecstūri 20 sešstūri | 90 | 60 |
|
| Rombikozidodekaedrs | 62 | 20 trīsstūri30 kvadrātiņi12 | 120 | 60 |
|
| Saīsināts ikozidodekaedrs | 62 | 30 laukumi 20 sešstūri 12 dekagoni | 180 | 120 |
|
| Snubveida dodekaedrs (2 spoguļattēlu versijas) | 92 | 80 trīsstūri 12 piecstūri | 150 | 60 |
Jautājumi un atbildes
J: Kas ir Arhimēda cietviela?
A: Arhimēda cietviela ir no daudzstūriem veidota izliekta figūra, kurai piemīt tādas īpašības: katra virsma ir regulārs daudzstūris, visi stūri izskatās vienādi, un tā nav platona cietviela, prizma vai antiprisma.
J: Cik ir Arhimēda cietvielu?
Atbilde: Atkarībā no tā, kā tās saskaita, ir trīspadsmit vai piecpadsmit Arhimēda cietvielas.
J: Kas atklāja Arhimēda cietvielas?
A: Arhimēda cietvielu nosaukums ir sengrieķu matemātiķa Arhimēda vārdā, kurš tās, iespējams, atklāja 3. gadsimtā pirms mūsu ēras.
J: Ko Paps no Aleksandrijas darīja ar Arhimēda rakstiem?
A: Papps no Aleksandrijas 4. gadsimtā apkopoja Arhimēda rakstīto par Arhimēda cietajām vielām.
J: Kāpēc mākslinieki un matemātiķi no jauna atklāja Arhimēda cietvielas renesanses laikā?
A: Renesanses laikā mākslinieki un matemātiķi augstu vērtēja tīras formas, un Arhimēda cietvielas tika uzskatītas par tīrām formām.
J: Kad Johannes Keplers pabeidza visu Arhimēda ķermeņu meklējumus?
A: Johannes Keplers, iespējams, pabeidza visu Arhimēda cietvielu meklējumus ap 1620. gadu.
J: Kas nepieciešams, lai izveidotu Arhimēda cietvielu?
A: Lai uzbūvētu Arhimēda cietvielu, ir vajadzīgi vismaz divi dažādi daudzstūri.
Meklēt