Gaismas pulkstenis: relativitātes princips un laika dilatācija

Gaismas pulkstenis: vienkārša relativitātes skaidrošana un laika dilatācijas izskaidrojums ar piemēriem un viegli saprotamiem aprēķiniem.

Gaismas pulkstenis ir vienkāršs un ilustratīvs veids, kā parādīt speciālās relativitātes pamatiezīmi. Šāda pulksteņa darbības princips ir vienkāršs: no staba apakšas tiek nosūtīts gaismas mirklis uz staba galā ievietotu spoguli, tas atstarojas un atgriežas pie detektora apakšā. Katrs šāds atspulgs tiek uzskatīts par vienu "tikšķi". Ja gaismas pulkstenis pārvietojas attiecībā pret novērotāju, novērotājam šķiet, ka pulksteņa "tikšķi" notiek lēnāk — šo parādību sauc par laikadilatāciju.

Lai labāk saprastu ideju, apskatīsim analoģiju. Iedomājieties basketbolistu, kurš driblē bumbu lielas kravas lidmašīnas kravas nodalījumā. Basketbolists un bumba kustas kopā ar lidmašīnu, tāpēc lidmašīnā esošie redz, ka bumba atlēkusi uz augšu un atpakaļ par metru vai diviem, un tas notiek aptuveni ik pēc vienas sekundes. Tomēr attiecībā pret Zemi bumbas horizontālā novietojuma maiņa var būt simtiem metru starp diviem atlēcieniem — tas parāda, ka relatīva kustība maina to, kā atsevišķus notikumus (šeit: divus atlēcienus) uztver dažādi novērotāji.

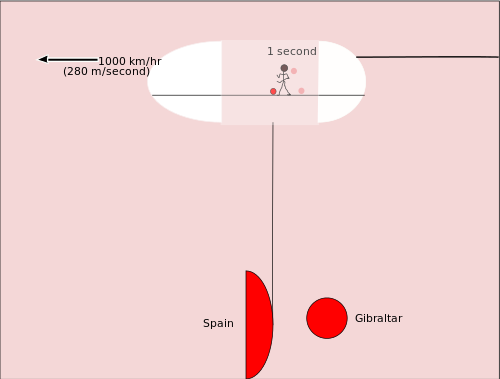
Tagad apskatīsim tieši gaismas pulksteņa gadījumu: zemes novērotāji (piemēram, no Ziemeļpola) vēro kosmosa kuģi, kurš pārvietojas horizontāli lielā ātrumā, un kuģī ir identisks gaismas pulkstenis. Lai aprēķinātu, cik daudz laika aizņem viens "tikšķis" novērotājiem uz Zemes, izmantojam vienkāršu attāluma–ātruma–laika sakarību:

d = r t

Šeit r apzīmē kosmosa kuģa ātrumu attiecībā pret Zemi (agrāk tekstā atzīmēts kā r), bet vēlāk izmantosim c gaismas ātrumam. Gaismas ātrums c ir konstants visos inerciālajos režģos — tas ir viens no speciālās relativitātes pamatprincipiem.

Stacionārā gaismas pulksteņa "tikšķis"

Ja pulkstenis stāv uz vietas (tas pats pulkstenis, ko pēc tam ieliek kosmosa kuģī), gaisma ceļo taisni uz augšu līdz spogulim un atpakaļ. Ja staba garums ir a, tad kopējais ceļš, ko gaisma veic vienā "tikšķī", ir d = 2a. Laiks starp diviem atgriezieniem (viena "tikšķa" ilgums) stacionārajā gadījumā ir

t = d / c = 2a / c.

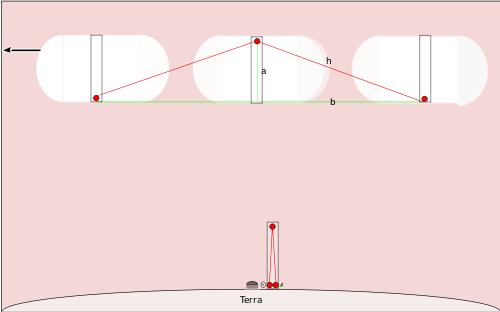
Gaismas pulkstenis, kas pārvietojas (diagrammas konstruēšana)

Ja pulkstenis atrodas kosmosa kuģī, kas pārvietojas ar ātrumu r paralēli Zemes virsmai, gaismas ceļš novērotājam uz Zemes izskatīsies diagonāls: kamēr gaismas mirklis ceļo uz spoguli un atpakaļ, pulkstenis horizontāli pārvietojas. Diagrammā puse no gaismas ceļa (no apakšas līdz spogulim) veido taisnstūra trijstūri ar vertikālo malu a un horizontālo malu (r t' / 2), ja t' apzīmē laiku starp "tikšķiem", mērītu novērotājiem uz Zemes.

Puse no gaismas ceļa (sauksim to par h) ir:

h = √( a² + ( (r t')/2 )² )

Tātad kopējais gaismas ceļš vienā "tikšķī", kā to redz zemes novērotājs, ir d = 2 h. Tāpat gaismas ātrums ir c, tāpēc šo ceļu var saistīt ar laiku t' šādi:

c t' = 2 √( a² + ( (r t')/2 )² )

Vienādojuma atrisināšana (īsa, skaidra algebra)

Sākam ar

c t' / 2 = √( a² + ( (r t')/2 )² )

Kvadrējot abas puses:

(c t' / 2)² = a² + (r t' / 2)²

Izvēršot:

c² t'² / 4 = a² + r² t'² / 4

Pārvietojot locekļus ar t'² vienā pusē:

(c² - r²) t'² / 4 = a²

No turienes:

t'² = 4 a² / (c² - r²)

Tātad

t' = 2 a / √(c² - r²) = (2 a / c) · 1 / √(1 - r²/c²)

Atceroties, ka stacionārā pulksteņa "tikšķa" ilgums ir t = 2 a / c, varam to ierakstīt vienkāršākā formā, izmantojot Lorenca faktoru:

t' = t / √(1 - r² / c²) = γ t

Šeit γ = 1 / √(1 - r² / c²) ir Lorenca faktors. Novērotājs uz Zemes redz, ka gaismas pulkstenis uz pārvietojošā kuģa "tikšķ" ilgst ilgāk nekā tas pats pulkstenis stāvot uz vietas — tukšuma laiks ir dilatēts.

Skaitlisks piemērs

Ja t = 1 sekunde (tas ir, ja stāvēšana pie Ziemeļpola radītu vienas sekundes starpību starp "tikšķiem"), un kuģa ātrums ir r = 0,5 c, tad

γ = 1 / √(1 - 0,5²) = 1 / √(1 - 0,25) = 1 / √0,75 ≈ 1,1547

Tātad novērotājam uz Zemes šāds pulkstenis būs redzams kā "tikšķinām" ar ilgumu

t' ≈ 1,1547 s.

Ko tas nozīmē un kāpēc tas ir svarīgi

• Laikadilatācija nozīmē, ka kustībā esošs pulkstenis šķiet, ka tas rit lēnāk salīdzinājumā ar novērotāja pulksteni. Šis rezultāts ir eksperimentāli apstiprināts (piemēram, ar ātri lidojošu daļiņu dzīves ilgumu novērošanu, atomu pulksteņu salīdzināšanu līdzenā kustībā u.c.).
• Gaismas ātruma invariance (c konstante visos inerciālajos režģos) ir pamatnosacījums, no kura izriet laika dilatācija — gaisma vienmēr iziet ar ātrumu c neatkarīgi no novērotāja kustības.
• Speciālās relativitātes sekas praktiski jāņem vērā, piemēram, GPS sistēmās, kur gan relativitātes efekti, gan gravitācijas laika nobīde ietekmē precizitāti.

Ja vēlaties eksperimentēt ar dažādiem ātrumiem un uzskatāmi redzēt laikadilatāciju, varat izmantot interaktīvos rīkus, piemēram: http://www.1728.org/reltivty.htm.

Saīsinot: gaismas pulkstenis ir skaidra ilustrācija tam, kā un kāpēc kustībā esoša laika intervāla mērījums kļūst garāks — precīzs izrietošais formulas rezultāts ir t' = t / √(1 - r²/c²), kur t ir laiks pulkstenim tā paša pulksteņa atpūtā un t' — laiks, ko to novēro kustībā attiecībā uz novērotāju.

Jautājumi un atbildes

J: Kas ir gaismas zvans?

J: Kas ir laika dilatācija?

J: Kā mēs varam aprēķināt, cik ļoti palēninās laiks kosmosa kuģī?

J: Kā darbojas gaismas pulkstenis?

J: Kāds vienādojums mums ir nepieciešams šim aprēķinam?

J. Kā Pitagora teorēma ir saistīta ar šo aprēķinu?

Meklēt pēc burta