Gravitācijas paātrinājums (g) — definīcija, Zemes vērtība un pielietojums

Uzzini gravitācijas paātrinājuma (g) definīciju, Zemes standartvērtību 9,80665 m/s² un praktiskos pielietojumus fizikā, inženierijā un ikdienā.

Autors: Leandro Alegsa

Paātrinājumu, ko objekts iegūst gravitācijas spēka dēļ, sauc par gravitācijas radīto paātrinājumu. Tā SI mērvienība ir m/s2. Gravitācijas spēka radītais paātrinājums ir vektors, kas nozīmē, ka tam ir gan lielums, gan virziens — vietēji tas norāda uz leju, proti, uz Zemes centru vai citām masas koncentrācijām. Gravitācijas spēka izraisīto paātrinājumu Zemes virsmā parasti apzīmē ar burtu g. Tā standartvērtība (starptautiskais konvencionālais vidējais rādītājs) ir 9,80665 m/s2 (32,1740 ft/s2), taču faktiskais paātrinājums brīvā kritienā mainās atkarībā no atrašanās vietas, augstuma un Zemes rotācijas.

Kas nosaka g vērtību

Galvenie faktori, kas nosaka g lielumu uz Zemes, ir:

  • Attālums līdz Zemes centram: gravitācijas paātrinājums aptuveni samazinās kā 1/r2, t.i., g ≈ G·M/r2, kur G ir gravitācijas konstante, M — Zemes masa un r — attālums no masas centra.
  • Zemes forma un blīvuma sadalījums: Zeme nav ideāls sfērisks ķermenis — tā ir sadrūzījusi (malskats), un blīvuma variācijas ietekmē lokālo g vērtību.
  • Zemes rotācija: centrifugālā paātrinājuma komponents samazina gravitācijas paātrinājumu, īpaši pie ekvatora. Tāpēc g ir mazāks pie ekvatora un lielāks pie poliem.

Tipiskas vērtības un to variācijas

Pie jūras līmeņa g vērtība svārstās aptuveni no 9,780 m/s2 (ekvatoriālā zona) līdz apmēram 9,832 m/s2 (polārajās teritorijās). Precīzāka izteiksme ņem vērā gan Zemes nogludināto formu, gan rotācijas ietekmi; piemēram, tipiskās vērtības ir:

  • ekvators: aptuveni 9,7803 m/s2,
  • vidusplatumi: apmēram 9,806 m/s2,
  • polu tuvums: aptuveni 9,8322 m/s2.

Augstumā g samazinās; aptuvena lineāra pieeja mazam augstumam h ir g(h) ≈ g0·(1 − 2h/R), kur R ir Zemes rādiuss (≈ 6,371 km). Precīzāk: g(h) = G·M/(R+h)2.

Formulas un vienkārši piemēri

  • Newtona gravitācijas likums: g = G·M/r2.
  • Svara saistība: objekta svars W = m·g — svaru izsaka spēkā (Ņūtonos), kur m ir objekta masa. Masa nemainās, bet svars atkarīgs no lokālās g vērtības.
  • Brīvā krišanas laiks: no attāluma h bez gaisa pretestības t = √(2h/g). Piemēram, no 100 m kritiena laiks aptuveni t ≈ √(200/9,81) ≈ 4,5 s.

Mērīšana un pielietojums

Gravitācijas paātrinājumu mēra ar gravimetriem — absolūtajiem (izmanto interferometriju vai svārstību periodu) un relatīvajiem (jutīgi svārstību mērierīces). Vēsturiski g noteica ar svārstbumbu perioda mērījumiem (tiešas gravitācijas novērtēšanas metodes).

Pielietojumi:

  • metrologija un kalibrēšana (standarta g izmanto atskaites punktos);
  • inženiertehniskie aprēķini (būvniecība, transports, drošība);
  • balistikas un lidojumu dinamika;
  • ģeofizika un prospekcionēšana — lokālas g izmaiņas norāda uz blīvuma anomālijām zemes garozā;
  • inertās navigācijas sistēmas un akselerometriem, kas mēra paātrinājumu attiecībā pret brīvi nokritušu rāmjiem;
  • astronautikā — izpratne par “apjoma smagumu” un mikrogravitāti Zemes orbītā (orbitālā bezsvara stāvoklī objekti ir brīvi krītoši).

Piezīmes un papildinformācija

  • Simbols: burtiskais apzīmējums ir g.
  • Standarta gravitācija: 9,80665 m/s2 ir definēta konvencijā un tiek lietota, piemēram, lai noteiktu masa/vara attiecības uz Zemes un kalibrētu mērierīces.
  • Vektora virziens: lokāli tas ir pretējs «vertikālei uz augšu»; inženierijā izmanto arī jēdzienu lokālais vertikāls vai «plumb line» (smaguma smilga), lai aprakstītu g virzienu.

Kāpēc smagāki objekti nekrīt ātrāk par vieglākiem objektiem

Īzaks Ņūtons noskaidroja, ka rezultantais spēks ir vienāds ar masas reizinājumu ar paātrinājumu jeb simbolos F = m a {\displaystyle F=ma}{\displaystyle F=ma} . To var pārkārtot, lai iegūtu a = F m {\displaystyle a={{\frac {F}{m}}}}} } {\displaystyle a={\frac {F}{m}}\ }. Jo lielāka ir krītošā objekta masa, jo lielāks ir gravitācijas pievilkšanas spēks, kas to velk uz Zemi. Iepriekš minētajā vienādojumā tas ir F {\displaystyle F}F . Tomēr tas, cik reižu spēks kļūst lielāks vai mazāks, ir vienāds ar to, cik reižu masa kļūst lielāka vai mazāka, attiecībai paliekot nemainīgai. Jebkurā situācijā F m {\displaystyle {\frac {F}{m}}}{\displaystyle {\frac {F}{m}}\ } anulē līdz vienādam paātrinājumam, kas ir aptuveni 9,8 m/s2 . Tas nozīmē, ka neatkarīgi no to masas visi brīvi krītošie objekti paātrinās ar vienādu ātrumu.

Aplūkojiet šādus piemērus:

a = 49 N 5 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}} =9,8\,\mathrm {N/kg} =9,8\,\mathrm {m/s^{2}}. } {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} }

a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}} =9,8\,\mathrm {N/kg} =9,8\,\mathrm {m/s^{2}}. } {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} }

Virsmas paātrinājums

Atkarībā no atrašanās vietas objekts uz Zemes virsmas krīt ar paātrinājumu no 9,76 līdz 9,83 m/s2 (32,0 līdz 32,3 ft/s2 ).

Zeme nav gluži sfēriska. Tā ir līdzīga "saspiestai" lodei, kuras rādiuss pie ekvatora ir nedaudz lielāks nekā rādiuss pie poliem. Tas nedaudz palielina gravitācijas paātrinājumu pie poliem (jo mēs atrodamies tuvu Zemes centram un gravitācijas spēks ir atkarīgs no attāluma) un nedaudz samazina to pie ekvatora. Turklāt, pateicoties centripetālajam paātrinājumam, gravitācijas spēka radītais paātrinājums ir nedaudz mazāks pie ekvatora nekā pie poliem. Zem zemes slāņu blīvuma izmaiņas vai kalnu klātbūtne tuvumā var nedaudz ietekmēt gravitācijas paātrinājumu.

Augstums

Objekta paātrinājums mainās atkarībā no augstuma. Gravitācijas paātrinājuma izmaiņas, mainoties attālumam no Zemes centra, atbilst apgriezto kvadrātu likumam. Tas nozīmē, ka gravitācijas paātrinājums ir apgriezti proporcionāls attāluma no Zemes centra kvadrātam. Attālumam dubultojoties, gravitācijas paātrinājums samazinās 4 reizes, attālumam trīskāršojoties, gravitācijas paātrinājums samazinās 9 reizes utt.

gravitācijas paātrinājums ∝ 1 attālums 2 {\displaystyle {\mbox{gravitācijas paātrinājums}}\ \\propto \ {\frac {1}{{{{\mbox{attālums}}}^{2}}}}\ } {\displaystyle {\mbox{gravitational acceleration}}\ \propto \ {\frac {1}{{\mbox{distance}}^{2}}}\ }

gravitācijas paātrinājums × attālums 2 = k {\displaystyle {\mbox{gravitācijas paātrinājums}}\ \\ reizes {{\mbox{attālums}}}^{2}}\ ={k}} {\displaystyle {\mbox{gravitational acceleration}}\ \times {{\mbox{distance}}^{2}}\ ={k}}

Zemes virspusē gravitācijas spēka radītais paātrinājums ir aptuveni 9,8 m/s2 (32 ft/s2 ). Vidējais attālums līdz Zemes centram ir 6371 km (3959 jūdzes).

k = 9,8 × 6371 2 {\displaystyle {k}={\mbox{9,8}}\ reizes {{\mbox{6371}}^{2}}}} {\displaystyle {k}={\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}

Izmantojot konstantu k {\displaystyle k} kvaram aprēķināt gravitācijas paātrinājumu noteiktā augstumā.

gravitācijas paātrinājums = k attālums 2 {\displaystyle {\mbox{gravitācijas paātrinājums}}} ={\frac {k}{{{\mbox{attālums}}}^{2}}}}}}\ } {\displaystyle {\mbox{gravitational acceleration}}\ ={\frac {k}{{\mbox{distance}}^{2}}}\ }

Piemērs: Atrodiet gravitācijas paātrinājumu 1000 km (620 jūdžu) augstumā virs Zemes virsmas.

6371 + 1000 = 7371 {\displaystyle 6371+1000=7371} {\displaystyle 6371+1000=7371}

∴ Attālums no Zemes centra ir 7 371 km.

gravitācijas paātrinājums = 9,8 × 6371 2 7371 2 ≈ 7,3 {\displaystyle {\\mbox{gravitācijas paātrinājums}}} = {{\frac {{\mbox{9,8}}} \\reiz {{\mbox{6371}}}^{2}}}}{{{\mbox{7371}}^{2}}}}\\\aprox 7,3} {\displaystyle {\mbox{gravitational acceleration}}\ ={\frac {{\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}{{\mbox{7371}}^{2}}}\ \approx 7.3}

∴ Gravitācijas spēka radītais paātrinājums 1000 km (620 jūdžu) augstumā virs Zemes virsmas ir 7,3 m/s2 (24 ft/s2 ).

Gravitācijas paātrinājums Karmana līnijā, kas ir robeža starp Zemes atmosfēru un kosmosu un atrodas 100 km (62 jūdžu) augstumā, ir tikai par aptuveni 3 % mazāks nekā jūras līmenī.

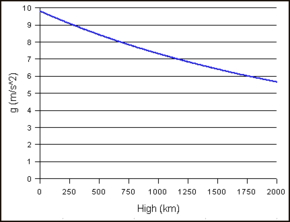
Gravitācijas paātrinājuma izmaiņas atkarībā no objekta augstumaZoom
Gravitācijas paātrinājuma izmaiņas atkarībā no objekta augstuma

Jautājumi un atbildes

J: Kas ir gravitācijas radītais paātrinājums?


A: Gravitācijas radītais paātrinājums ir paātrinājums, ko objekts iegūst gravitācijas spēka iedarbības dēļ.

J: Kāda ir gravitācijas spēka radītā paātrinājuma SI mērvienība?


A: Smaguma spēka radītā paātrinājuma SI vienība ir m/s2.

J: Vai gravitācijas paātrinājums ir skalārs vai vektors?


A: Gravitācijas izraisītais paātrinājums ir vektors, jo tam ir gan lielums, gan virziens.

J: Ar kādu simbolu apzīmē gravitācijas paātrinājumu uz Zemes virsmas?


A: Simbols, ar ko apzīmē gravitācijas radīto paātrinājumu Zemes virspusē, ir g.

J: Kāda ir Zemes virsmas gravitācijas paātrinājuma standartvērtība?


A: Zemes virsmas gravitācijas paātrinājuma standarta vērtība ir 9,80665 m/s2 (32,1740 ft/s2).

J: Vai brīvi krītoša ķermeņa faktiskais paātrinājums mainās atkarībā no atrašanās vietas?


A: Jā, brīvā kritienā esoša ķermeņa faktiskais paātrinājums mainās atkarībā no atrašanās vietas.

J: Kāda ir smaguma spēka radītā paātrinājuma definīcija?


A: Gravitācijas spēka izraisītais paātrinājums ir paātrinājums, ko objekts iegūst gravitācijas spēka iedarbības dēļ, un to apzīmē ar burtu g ar standarta vērtību 9,80665 m/s2 uz Zemes virsmas, bet faktiskais paātrinājums var mainīties atkarībā no atrašanās vietas.


Meklēt
AlegsaOnline.com - 2020 / 2025 - License CC3