Paralēlais postulāts — Eiklīda piektais postulāts ģeometrijā
Iepazīsties ar Paralēlo postulātu — Eiklīda piekto postulātu ģeometrijā: skaidrojums, piemēri, nozīme un neeiklīdiskās alternatīvas saprotamā valodā.
Ģeometrijā paralēles postulāts ir viena no Eiklīda ģeometrijas aksiomām. Dažkārt to dēvē arī par piekto Eiklīda postulātu, jo tas ir piektais postulāts Eiklīda "Elementos".
Postulāts saka, ka:
Ja nogriežat taisni ar divām līnijām un divi iekšējie leņķi, ko veido šīs līnijas, ir mazāki par 180°, tad abas līnijas galu galā satiksies, ja tās pagarināsiet pietiekami ilgi.
Ģeometrijas jomu, kurā ievērotas visas Eiklīda aksiomas, sauc par Eiklīda ģeometriju. Ģeometriju, kurā netiek ievērotas visas Eiklīda aksiomas, sauc par neeiklīda ģeometriju.
Vēsture un nozīme
Vēsturiski piektais postulāts Eiklīdam šķita mazāk pašsaprotams nekā pārējie postulāti, tāpēc daudzi matemātiķi mēģināja to pierādīt, izmantojot pārējos postulātus. Šīs mēģinājumu pēdas ved cauri gadsimtiem — no antīkajiem un viduslaiku ģeometriķiem līdz 18.—19. gadsimtam. 19. gadsimtā matemātiķi kā Niels Henrik Abel, Jānis Boljajs (János Bolyai), Kārls Frīdrihs Gause un Lobačevskis (Nikolajs Lobačevskis) neatkarīgi parādīja, ka piektais postulāts ir neatkarīgs no pārējiem Eiklīda aksiomām: no pārējām aksiomām nevar izrēķināt vai pierādīt piekto. Tas atklāja jaunas ģeometrijas — neeiklīda ģeometrijas, kurās piektais postulāts nav spēkā.
Mūsdienu formulējumi
Mūsdienās bieži lieto ekvivalentu un vienkāršāku formulējumu, kas saucas Playfair aksioma:
- Dotai taisnei un punktam ārpus tās eksistē vienīgi viena taisne, kas iet caur šo punktu un nav vardarbīgi pret šo taisni (tj., ir paralēla tai).
Playfair formulējums ir ekvivalents Eiklīda piektajam postulātam, ja pārējās Eiklīda aksiomas tiek pieņemtas.
Ekvivalenti apgalvojumi un sekojošie īpašumi
Daudzi naturāli ģeometrijas apgalvojumi izrādās ekvivalenti piektajam postulātam (atkal pieņemot pārējās Eiklīda aksiomas). Starp tiem ir:
- Trijstūra iekšējo leņķu summa vienmēr ir 180°.
- Eksistē taisnstūri (līdz ar to arī paralēlu taisnju pāris, kas uztur taisnus leņķus).
- Ja divas taisnes ir paralēlas trešajai, tad tās savā starpā ir paralēlas.
- Veidojas standarta līdzības attiecības — var pastāvēt līdzīgi (bet nekonkrīgu) trijstūri.
Visi šie apgalvojumi parādās vai pazūd atkarībā no tā, vai pieņem piekto postulātu.
Neeiklīda ģeometrijas piemēri
- Hiperboliskā ģeometrija (Lobačevska ģeometrija): caur dotu punktu ārpus dotas taisnes var vilkt vairākas taisnes, kas nekrustojas ar doto taisni — tātad paralēlu ir vairāk nekā viena. Trijstūru iekšējo leņķu summa ir mazāka par 180°.
- Eliptiskā ģeometrija (piemēram, sfēras ģeometrija ar lielajām lokiem): nekādas divas "taisnes" (lielie loki) nesaglabā paralelitāti — jebkuras divas vietām krustojas, tātad nav paralēļu. Trijstūru iekšējo leņķu summa ir lielāka par 180°.
Modeļi un konsistence
19. gadsimta atklājumi parādīja, ka, ja Eiklīda aksiomu kopa bez piektā postulāta ir konsekventa, tad arī papildinājums ar piekto postulātu un papildinājums ar tā noliegumu būs konsekventi. To apliecināja konkrēti modeļi:
- Poincaré disks un Beltrami–Klein modelis — modeļi hiperboliskajai ģeometrijai, kas demonstrē hiperboliskās aksiomas konsistenci (attiecībā pret eiklīdisko metamatemātiku).
- Sfēra ar lielajiem lokiem kā "taisnēm" ir piemērs eliptiskajai ģeometrijai.
Sekas praksē
Piektais postulāts ietekmē daudz praktisku un teorētisku jomu: no klasiskās ģeometrijas konstruēšanas un trijstūru teorijas līdz ģeometrijas pamatidejām modernās fizikā (piem., telpas curving in vispārējā relativitātē ļauj citus attēlojumus). Sapratne, ka piektais postulāts nav pašsaprotams, lika matemātiķiem attīstīt plašāku ģeometriju spektru un skaidri nošķirt aksiomas no pēctecībām un secinājumiem.
Kur lasīt vairāk
Cilvēkiem, kuri vēlas padziļināt izpratni, ieteicams meklēt literatūru par Eiklīda Elementiem, par Lobačevska un Boljaja darbu hiperboliskajā ģeometrijā, kā arī par moderniem modeļiem (Poincaré disks, Beltrami modelis). Šie avoti palīdz saprast gan idejas, gan formālo pierādīšanas gājienu, kādēļ piektais postulāts ir tik īpašs matemātikā.
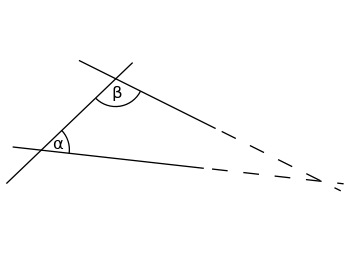
Ja iekšējo leņķu α (alfa) un β (beta) summa ir mazāka par 180°, abas taisnes kaut kur krustojas, ja abas ir pagarinātas līdz bezgalībai.
Vēsture
Daži matemātiķi uzskatīja, ka Eiklīda piektais postulāts ir daudz garāks un sarežģītāks nekā pārējie četri postulāti. Daudzi no viņiem uzskatīja, ka to var pierādīt, pamatojoties uz citām vienkāršākām aksiomām. Daži matemātiķi paziņoja, ka ir pierādījuši šo postulātu no vienkāršākiem postulātiem, taču izrādījās, ka viņi visi ir kļūdījušies.
Playfēra aksioma
Vēl viens jaunāks apgalvojums, pazīstams kā Playfēra aksioma, ir līdzīgs Eiklīda piektajam postulātam. Tajā teikts, ka:
Ja ir dota taisna līnija un punkts, kas neatrodas uz šīs līnijas, caur šo punktu var novilkt tikai vienu taisnu līniju, kas nesaskan ar otru taisnu līniju.
Patiesībā matemātiķi atklāja, ka šī aksioma ir ne tikai līdzīga Eiklīda piektajam postulātam, bet tai ir tieši tāda pati nozīme. Matemātiski šos divus apgalvojumus sauc par "ekvivalentiem" apgalvojumiem. Mūsdienās matemātiķi biežāk izmanto Playfēra aksiomu nekā sākotnējo Eiklīda paralēlo postulātu.
Neeiklīda ģeometrija
Galu galā daži matemātiķi mēģināja izveidot jaunas ģeometrijas, neizmantojot aksiomu. Vienu no neeiklīda ģeometrijas veidiem sauc par eliptisko ģeometriju. Eliptiskajā ģeometrijā paralēles postulāts ir aizstāts ar aksiomu, kas nosaka, ka:
Ja ir dota taisna līnija un punkts, kas neatrodas uz šīs līnijas, caur šo punktu nevar novilkt taisnu līniju, kas galu galā nešķērsotu otru taisni.
Matemātiķi atklāja, ka, aizvietojot Eiklīda piekto postulātu ar šo aksiomu, viņi joprojām varēja pierādīt daudzas citas Eiklīda teorēmas. Viens no veidiem, kā iztēloties eliptisko ģeometriju, ir domāt par zemeslodes virsmu. Uz zemeslodes garuma līnijas šķiet paralēlas pie ekvatora, bet visas tās satiekas pie poliem. 19. gadsimta beigās tika pierādīts, ka eliptiskā ģeometrija ir konsekventa. Tas pierādīja, ka Eiklīda piektais postulāts nav neatkarīgs no pārējiem postulātiem. Pēc tam matemātiķi lielākoties pārstāja mēģināt pierādīt piekto postulātu no pārējiem četriem postulātiem. Tā vietā daudzi matemātiķi sāka pētīt citas ģeometrijas, kas neatbilst Eiklīda piektajam postulātam.
Cita aksioma, ar kuru matemātiķi dažkārt aizstāj Eiklīda piekto aksiomu, ir šāda:
Ja ir dota taisna līnija un punkts, kas neatrodas uz šīs līnijas, var uzzīmēt vismaz divas taisnas līnijas caur šo punktu, kas galu galā nešķērsos otru taisni.
To sauc par hiperbolisko ģeometriju.
Cita ģeometrija vienkārši atceļ Eiklīda piekto postulātu un ne ar ko to neaizstāj. To sauc par neitrālo ģeometriju jeb absolūto ģeometriju.
Meklēt