Cilindrs — definīcija, veidi, laukums un tilpums
Cilindrs — skaidra definīcija, cilindru veidi, formulas virsmas laukuma un tilpuma aprēķināšanai, piemēri un vizualizācijas gan ikdienai, gan matemātikai.
Cilindrs ir viena no visvienkāršākajām izliektajām ģeometriskām figūrām, kuras virsmu veido punkti, kas atrodas noteiktā attālumā no dotās taisnes, ko sauc par cilindra asi. Šo figūru var uzskatīt par apaļu prizmu. Par cilindru var saukt gan virsmu, gan iekšpusē izveidoto cieto figūru. Cilindra virsmas laukums un tilpums ir zināms jau kopš seniem laikiem.
Diferenciālajā ģeometrijā cilindrs ir plašāk definēts kā jebkura regulēta virsma, ko šķērso viena parametra paralēlo līniju saime. Cilindru, kura šķērsgriezums ir elipse, parabola vai hiperbola, sauc attiecīgi par eliptisko cilindru, parabolisko cilindru vai hiperbolisko cilindru.
Cilindra daļas un termini
- Asi — taisne, attiecībā uz kuru cilindrā visi ģeneratori (paralēlās rindas) ir vienā attālumā.
- Bāzes (pamatnes) — divas paralēlas līnijas vai līknes (parasti riņķi vai elipses), kas savienotas ar ģeneratoriem; cietā cilindrā tās ir divas plaknes daļas.
- Ģenerators (ģeneratīvlīnija) — taisne, kas iet paralēli asij un veido cilindru, šo taisni bieži sauc par sānu līniju.
- Augstums (h) — attālums starp pamatnēm mērāms pa perpendikulāru; pareizā cilindrā tas sakrīt ar asu garumu.
- Rādiuss (r) — attālums no centra līdz pamatnes malai (apļu gadījumā).
Veidi
- Pareizais (perpendikulārais) cilindrs — ģeneratori ir perpendikulāri pamatnēm; bāzes ir paralēlas un tieši viena virs otras. Biežāk sastopamais gadījums ir pareizais apaļais cilindrs, kur pamatnes ir apļi.
- Slīpais (nekoreizais) cilindrs — ģeneratori nav perpendikulāri pamatnēm; pamatnes ir paralēlas, bet viens bāzes centrs ir nobīdīts attiecībā pret otru.
- Eliptiskais, paraboliskais un hiperboliskais cilindrs — nosaka pēc šķērsgriezuma formas (elipse, parabola, hiperbola). Šie cilindri parādās gan tīrajā matemātikā, gan inženiertehnikā.
Laukums un tilpums — galvenās formulas
Visvienkāršākajā — pareizā apaļā cilindrā ar pamatnes rādiusu r un augstumu h — formas un tilpuma formulas ir:
- Pamatnes laukums: A_p = π r²
- Sānu (manteles) laukums: A_m = 2 π r h (tas ir apļa apkārtmērs reiz augstums)
- Kopējais virsmas laukums: A_tot = 2 A_p + A_m = 2 π r (r + h)
- Tilpums: V = A_p · h = π r² h
Svarīgi: šīs formulas der pareizajam cylinderam. Slīpa cilindrā tilpums joprojām ir V = (pamatnes laukums) · (perpendikulārais augstums) — tātad tilpums no pamatnes laukuma reizināts ar perpendikulāro attālumu starp pamatnēm. Tas izriet no Cavalieri principa.
Eliptiskā cilindra formulas
Ja pamatne ir elipse ar pusass a un b, tad pamatnes laukums ir A_p = π a b, un tilpums ir V = π a b h. Manteles laukumu var izteikt kā elipses apkārtmēra P_e reiz augstums: A_m = P_e · h, taču elipses apkārtmēram nav vienkāršas eksaktas elementāras formulas — bieži izmanto aptuvenas formulas (piem., Ramanujan aproksimācija).
Aprēķinu piemērs
Ja pareizam apaļam cilindram r = 3 cm un h = 10 cm, tad:
- A_p = π · 3² = 9π cm² ≈ 28.27 cm²
- A_m = 2π · 3 · 10 = 60π cm² ≈ 188.50 cm²
- A_tot = 2·9π + 60π = 78π cm² ≈ 245.77 cm²
- V = π · 3² · 10 = 90π cm³ ≈ 282.74 cm³
Neto (cilindra aploksne)
Cilindra aploksne (virskārta) ir taisnstūris ar izmēriem augstums h un platums 2πr, kuram abās malās pievienotas divas pamatnes (apļi vai citādas līknes). Šo neto viegli uzskatīt par elementāru līmējamā materiāla aprēķinu piemēru.
Pielietojumi un novērojumi
- Cilindriskas formas sastopamas ikdienā (skārdenes, tējas kannas, caurules), inženierijā un arhitektūrā.
- Cilindra tilpuma formula ļauj vienkārši aprēķināt šķidrumu daudzumu, ko var saturēt konteiners.
- Diferenciālajā ģeometrijā cilindrs kalpo kā vienkāršs piemērs izliektai virsmai ar nulles ģeometrisko izliekumu vienā virzienā.
Ja nepieciešams, varam pievienot attēlu (neto vai 3D skatu), detalizētu izvērtējumu slīpa cilindra īpašībām vai matemātisku atvasinājumu no integrāļiem un Cavalieri principa.
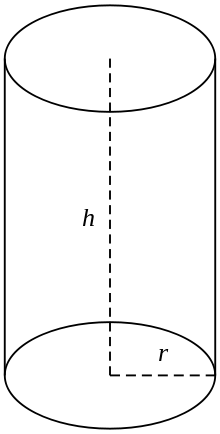
Taisnais apaļais cilindrs
Bieži lietots
Parasti ar cilindru apzīmē taisna apļa cilindra galīgo šķērsgriezumu, t. i., cilindru, kura ģenerējošās līnijas ir perpendikulāras pamatnēm, un kura gali ir noslēgti, veidojot divas apļveida virsmas, kā attēlā (pa labi). Ja cilindram ir r r rādiuss un garums (augstums) h, tad tā tilpums ir dots ar:
V = πrh2
un tā virsmas laukums ir:
- augšdaļas laukums (πr2) +
- dibena laukums (πr2) +
- sānu laukums (2πrh).
Tāpēc bez augšējās vai apakšējās daļas (sānu laukums) virsmas laukums ir:
A = 2πrh.
Ar augšējo un apakšējo daļu virsmas laukums ir:
A = 2πr2 + 2πrh = 2πr(r + h).
Dotajam tilpumam cilindram ar vismazāko virsmas laukumu ir h = 2r. Dotajam virsmas laukumam cilindram ar lielāko tilpumu ir h = 2r, t. i., cilindrs ietilpst kubā (augstums = diametrs).
Tilpums
Ir taisns apaļš cilindrs ar augstumu h vienību un pamatni ar r vienību rādiusu, kura koordinātu asis izvēlētas tā, ka sākumpunkts ir vienas pamatnes centrā un augstums tiek mērīts pa pozitīvo x asi. Plaknes šķērsgriezumam x vienību attālumā no sākuma ir laukums A(x) kvadrātvienību, kur
A ( x ) = π r {\displaystyle2 A(x)=\pi r^{2}}
vai
A ( y ) = π r {\displaystyle2 A(y)=\pi r^{2}}
Tilpuma elements ir taisnais cilindrs ar pamatnes laukumu Awi kvadrātvienības un biezumu Δxi vienības. Tātad, ja V kubikvienības ir labā apļveida cilindra tilpums, tad, izmantojot Rīmana summas,
C i l i n d e r v o l u m e = lim | | Δ → |0 | ∑ i = n 1A ( w i ) Δ i x {\displaystyle \mathrm {Tilpums\;no\;cilindrs} =\lim _{{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x}
= ∫0 h A ( y ) d2 y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy}
= ∫ 0h π r d 2y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Izmantojot cilindriskās koordinātas, tilpumu var aprēķināt, integrējot caur
= ∫ 0h0 ∫ 2π ∫ 0r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s,\,ds\,d\phi \,dz}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Cilindriskais šķērsgriezums
Cilindriskie griezumi ir cilindru krustpunkti ar plaknēm. Pareizajam apaļajam cilindram ir četras iespējas. plakne, kas ir cilindram pieskaras, krustojas ar cilindru vienā taisnā līnijā. Kad plakne ir paralēla pati sev, tā vai nu nešķērso cilindru, vai arī šķērso to divās paralēlās līnijās. Visas pārējās plaknes krustojas ar cilindru elipsei vai, ja tās ir perpendikulāras cilindra asij, - aplim.
Cita veida baloni
Elipsveida cilindrs jeb cilindroīds ir kvadriska virsma ar šādu vienādojumu Dekarta koordinātēs:
( x a ) +2 ( y b ) =21 . {\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=1.}
Šis vienādojums attiecas uz eliptisku cilindru, kas ir parastā apaļā cilindra (a = b) vispārinājums. Vēl vispārīgāks ir vispārinātais cilindrs: šķērsgriezums var būt jebkura līkne.
Cilindrs ir deģenerēts kvadriks, jo vismaz viena no koordinātēm (šajā gadījumā z) vienādojumā neparādās.
Slīpā cilindra augšējā un apakšējā virsma ir novietotas viena no otras.
Ir arī citi neparastāki balonu veidi. Tie ir iedomāti eliptiskie cilindri:
( x a ) +2 ( y b ) =2 - 1{\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=-1}}
hiperboliskais cilindrs:
( x a )2 - ( y b ) = 2{\displaystyle1 \left({\frac {x}{a}}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1}}
un paraboliskais cilindrs:
x +2 a 2y =0 . {\displaystyle x^{2}+2ay=0.\,}

Elipsveida cilindrs

Projektīvajā ģeometrijā cilindrs ir vienkārši konuss, kura virsotne ir bezgalībā, kas vizuāli atbilst cilindram perspektīvā, kas izskatās kā konuss pret debesīm.
Projektīvā ģeometrija
Projektīvajā ģeometrijā cilindrs ir vienkārši konuss, kura virsotne atrodas bezgalībā.
Tas ir noderīgi, definējot deģenerētos konususus, kas prasa ņemt vērā cilindriskos konususus.
Meklēt










