Zelta griezums
Izmantojot vienu skaitli a un citu mazāku skaitli b, abu skaitļu attiecību iegūst, tos dalot. To attiecība ir a/b. Citu attiecību atrod, saskaitot abus skaitļus a+b un dalot ar lielāko skaitli a. Jaunā attiecība ir (a+b)/a. Ja šīs divas attiecības ir vienādas ar vienu un to pašu skaitli, tad šo skaitli sauc par zelta attiecību. Grieķu burts φ {\displaystyle \varphi } 
(phi) parasti lieto kā zelta attiecības nosaukumu.
Piemēram, ja b = 1 un a/b = φ {\displaystyle \varphi } , tad a = φ {\displaystyle \varphi } . Otrā attiecība (a+b)/a tad ir ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi }. 
. Tā kā šie divi koeficienti ir vienādi, tas ir taisnība:
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}
Viens no veidiem, kā šo skaitli pierakstīt, ir šāds.
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\qrt {5}}}{2}}}}
5 {\displaystyle {\sqrt {5}}}
ir kā jebkurš skaitlis, ko reizinot ar sevi, iegūst 5 (vai arī kāds skaitlis tiek reizināts): 5 × 5 = 5 {\displaystyle {\sqrt {5}} reizes {\sqrt {5}}=5}}
.
Zelta griezums ir iracionāls skaitlis. Ja cilvēks mēģinās to uzrakstīt, tas nekad neapstāsies un nekad neveidos zīmējumu, bet sāksies šādi: 1,6180339887... Svarīga lieta par šo skaitli ir tā, ka cilvēks no tā var atņemt 1 vai dalīt 1 ar to. Jebkurā gadījumā skaitlis joprojām turpinās kustēties un nekad neapstāsies.
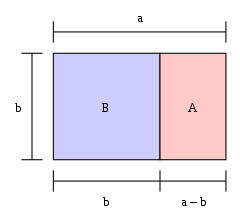
Zelta taisnstūris
Ja taisnstūra garums, dalīts ar tā platumu, ir vienāds ar zelta attiecību, tad taisnstūris ir "zelta taisnstūris". Ja no zelta taisnstūra viena gala nogriež kvadrātu, tad otrs gals ir jauns zelta taisnstūris. Attēlā lielais taisnstūris (zilais un rozā kopā) ir zelta taisnstūris, jo a / b = φ {\displaystyle a/b=\varphi }. 
. Zilā daļa (B) ir kvadrāts. Rozā daļa pati par sevi (A) ir vēl viens zelta taisnstūris, jo b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi }. 
. Lielajam taisnstūrim un rozā taisnstūrim ir vienāda forma, bet rozā taisnstūris ir mazāks un ir pagriezts.
Lielais taisnstūris BA ir zelta taisnstūris, tas ir, proporcija b:a ir 1: φ {\displaystyle \varphi } . Jebkuram šādam taisnstūrim, un tikai taisnstūriem ar šādu konkrētu proporciju, ja mēs noņemam kvadrātu B, tad tas, kas paliek A, ir vēl viens zelta taisnstūris, tas ir, ar tādām pašām proporcijām kā sākotnējam taisnstūrim.
Fibonači skaitļi
Fibonači skaitļi ir skaitļu saraksts. Cilvēks var atrast nākamo skaitli sarakstā, saskaitot divus pēdējos skaitļus kopā. Ja cilvēks dalīs skaitli sarakstā ar skaitli, kas bija pirms tā, šī attiecība arvien vairāk tuvosies zelta griezumam.
| Fibonači skaitlis | dalīts ar iepriekšējo | attiecība |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\displaystyle \varphi } | = 1.6180... |
Zelta attiecība dabā
Dabā zelta vidusdaļu bieži izmanto lapu vai ziedu sakārtojumā. Tajos izmanto zelta leņķi, kas ir aptuveni 137,5 grādi. Šādā leņķī sakārtotas lapas vai ziedi vislabāk izmanto saules gaismu.
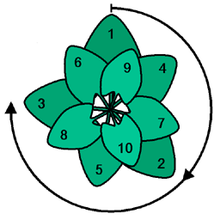
Izmantojot zelta leņķi, optimāli izmantosiet saules gaismu. Šis ir skats no augšas.
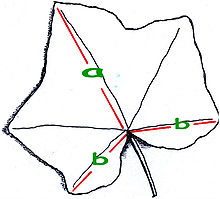
Parastā efejas lapa, uz kuras redzams zelta griezums
Jautājumi un atbildes
J: Kāda ir divu skaitļu attiecība?
A: Divu skaitļu attiecību atrod, tos dalot, tātad attiecība būtu a/b.
J: Kā var atrast citu attiecību?
A: Citu attiecību var atrast, saskaitot abus skaitļus kopā un pēc tam dalot šo summu ar lielāko skaitli a. Šī jaunā attiecība būtu (a+b)/a.
J: Kā sauc gadījumu, kad šīs divas attiecības ir vienādas?
A: Ja šīs divas attiecības ir vienādas, to sauc par zelta attiecību. To parasti apzīmē ar grieķu burtu צ vai phi.
J: Ja b = 1 un a/b = צ , ko tas nozīmē attiecībā uz a?
A: Ja b = 1 un a/b = צ , tad tas nozīmē, ka arī a = צ .
J: Kā šo skaitli var pierakstīt?
A: Viens no veidiem, kā šo skaitli var uzrakstīt, ir צ = 1 + 5 / 2 = 1,618...
J: Ko nozīmē, ja no tā atņem 1 vai dala 1 ar to?
A: Ja no tā atņemsi 1 vai ar to izdalīsi 1, iegūsi atpakaļ to pašu skaitli - citiem vārdiem sakot, abi skaitļi būs vienādi ar zelta griezumu.
J: Vai zelta attiecība ir iracionāls skaitlis?
A: Jā, zelta attiecība ir iracionāls skaitlis, un tas nozīmē, ka, ja kāds mēģinās to uzrakstīt, nekad nebūs ne gala, ne parauga - tikai sākas ar kaut ko līdzīgu "1,6180339887...".
