Lavīnas efekts kriptogrāfijā: definīcija un nozīme bloka šifros
Lavīnas efekts kriptogrāfijā: kā nelielas izmaiņas rada milzīgu drošību — definīcija, nozīme bloka šifros un praktiskas implikācijas efektīvai aizsardzībai.
Lavīnas efekts ("lavīnas efekts") ir blokķīferu un kriptogrāfisko hash funkciju (algoritmu) svarīga īpašība. Tā apraksta situāciju, kad pat neliela ievades izmaiņa (piemēram, viens bita) izraisa būtiskas un plaši izplatītas izmaiņas izejā. Kriptogrāfijā to parasti uzskata par vēlamu — labam šifram vai hash funkcijai vajadzētu nodrošināt, ka nelielas izmaiņas atslēgā vai atklātajā tekstā izraisa spēcīgas un neparedzamas izmaiņas šifrtekstā.
Kā tas darbojas
Lavīnas efekts parasti rodas no algoritmu iteratīvās struktūras un no elementiem, kas nodrošina jaukšanu un difūziju. Produktu šifri (piem., Feistela tipa vai substitution–permutation network) apvieno nepārskatāmus matemātiskus elementus — S-kastītes (substitūcijas), P-kastītes (permutācijas) un XOR operācijas — tā, lai katrs izejas bits pakāpeniski kļūtu atkarīgs no katra ieejas bita. Terminu "lavīnas efekts" pirmais lietoja Horsts Feistels (Feistel 1973). Vēlāk šo jēdzienu saistīja ar Šenona sajaukšanas īpašību.
Mērīšana un kriteriji
Praktiski lavīnas efektu mēra ar statistiskiem testiem. Viens izplatīts mērķis ir, lai, mainot vienu ievades bitu, katrs izejas bits mainītos ar aptuveni 50% varbūtību (t.i., apmēram puse bitu tiktu "uzlēkta"). Šādam uzvedībai atbilst tādas formulācijas kā Strict Avalanche Criterion (SAC). Arī Bit Independence Criterion (BIC) var tikt lietots, lai pārbaudītu, vai dažādu ievades bitu izmaiņu ietekmes uz diviem izejas biti ir savstarpēji neatkarīgas. Lai konstatētu novirzes no ideāla lavīnas uzvedības, tiek veikti lielu paraugu statistikas testi.
Nozīme drošībā
Ja bloka šifrs vai kriptogrāfiskā šifrēšanas funkcija būtiski neatbilst lavīnas efektam, tā ir vāja randomizācija. Tas nozīmē, ka kriptoanalītiķis var veikt prognozes par ievadi, pat ja pieejama tikai izeja. Šādas nelinearitātes vai strukturālas vājības var atvieglot diferencialās vai lineārās kriptoanalīzes metodes, kā arī atklāt atšķirības no gaidāmā "gadījuma" uzvedības, kas var novest pie daļējas vai pilnīgas atslēgas atklāšanas. Tāpēc lavīnas efekts ir viens no primārajiem projektēšanas mērķiem, radot spēcīgu šifru vai kriptogrāfisko šifrēšanas funkciju.
Dizaina prakse un paraugi
- Produktu šifri (piem., Feistela tīklos balstīti risinājumi) tiek projektēti tā, lai iterācijas pakāpeniski izplatītu ievades izmaiņas visā blokā — tā nodrošinot lavīnas efektu.
- SPN (substitution–permutation networks), ko izmanto, piemēram, AES, apvieno S-kastītes un bitu permutācijas, lai sasniegtu gan lielu nelinearitāti, gan difūziju.
- Hash funkcijām parasti ir lieli datu bloki un sarežģītas kompresijas funkcijas, lai pat neliela novirze ievadē radītu pilnīgi citu hash vērtību.
Kas jāņem vērā — ierobežojumi
Tomēr ir svarīgi saprast, ka pati lavīnas īpašība nav pietiekama drošībai. Labiem kriptogrāfiskiem konstruktiem jānodrošina arī citi īpašumi: augsta nelinearitāte, pretestība pret diferencialo un lineāro kriptoanalīzi, atslēgas garuma un struktūras pareiza izvēle u.c. Vāji dizainēts elements var parādīt "lokālu" lavīnu (daļēja izplatība), kas joprojām ļauj atrast vājās vietas.
Kā pārbaudīt lavīnas efektu praksē
- Veikt simulācijas: ģenerēt daudzas ievades, mainīt pa vienam bitam un skaitīt, cik izejas biti mainās.
- Aprēķināt atšķirību varbūtības un salīdzināt ar ideālo 50% vērtību; statistiski novirzes var liecināt par problemātiskām vietām.
- Papildus testiem izmēģināt algoritmu pret pazīstamām kriptoanalītiskām metodēm (diferenciālā, lineārā analīze u.c.), lai pārliecinātos, ka lavīnas uzvedība patiešām veicina drošību.
Kopsavilkumā: lavīnas efekts ir būtisks rādītājs kriptogrāfisku algoritmu kvalitatīvai uzvedībai — tas nodrošina, ka mazas ievades izmaiņas noved pie lielām, nejaušām izmaiņām izejā. Tomēr to jāvērtē kopā ar citiem drošības kritērijiem, lai nodrošinātu patiesi drošu dizainu.
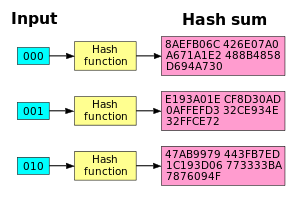
SHA1 hash funkcijai ir labs lavīnas efekts. Ja tiek izmainīts tikai viens bits, hash summa kļūst pilnīgi atšķirīga.
Nosaukums
Nosaukuma izcelsme ir zemes nogruvumi. Neliels iezis var nokrist, kopā ar sniegu un radīt postošu zemes nogruvumu. Akmens bija neliels, bet varēja radīt daudz postījumu. Tas ir tas pats, ko dara šis efekts. Nelielām izmaiņām ieejā (akmenī) jāmaina izejas rezultāts (ainava).
Stingrs lavīnas kritērijs
Strict Avalanche Criterion (SAC; "spēcīgs nogruvuma kritērijs") ir bolu funkciju īpašība. Tas ir svarīgs kriptogrāfijā. Tas ir izpildīts, ja visi izejas biti mainās ar 50 % varbūtību, ja tiek mainīts viens ieejas bits.
SAC tika veidota, pamatojoties uz evolūcijas pilnīguma un lavīnas jēdzieniem. To 1985. gadā ieviesa Vebsters un Tavaress. Mūsdienās tā ir prasība katrai modernai kriptogrāfijas sistēmai. To, piemēram, ir izpildījuši visi AES konkursa finālisti.
Bitu neatkarības kritērijs
Bitu neatkarības kritērijs (BIC; no bita neatkarīgs kritērijs) ir kritērijs. Tas ir šāds: Ja tiek mainīts (invertēts) viens ieejas bits, diviem izejas bitiem jāmainās neatkarīgi vienam no otra. Tas attiecas uz visiem bitiem.
Tas, piemēram, netiktu izpildīts, ja viens izejas bits mainītos tikai tad, ja mainītos arī otrs izejas bits. Tie varētu mainīties tikai tāpēc, ka mainījies ieejas bits. Pretējā gadījumā izejas biti būtu atkarīgi viens no otra.
Saistītās lapas
- Apjukums un difūzija
Jautājumi un atbildes
J: Kas ir lavīnas efekts?
A: Lavīnas efekts (pazīstams arī kā "lavīnas efekts") ir bloku šifru un kriptogrāfisko hash funkciju algoritmu īpašība, kas nosaka, ka nelielām izmaiņām atslēgā vai atklātajā tekstā vajadzētu izraisīt spēcīgas izmaiņas šifrtekstā.
J: Kurš pirmais lietoja terminu "lavīnas efekts"?
A: Terminu "lavīnas efekts" 1973. gadā pirmais lietoja Horsts Feistels.
J: Kā tas ir saistīts ar Šenona sajaukšanas īpašību?
A: Lavīnas efekta jēdziens tika identificēts ar Šenona sajaukšanas īpašību, kas nosaka, ka, ja bloka šifrs vai kriptogrāfiskā šifrēšanas funkcija būtiski neatbilst šai pakāpei, tad tai ir slikta randomizācija un to var daļēji vai pilnībā salauzt (uzlauzt).
J: Kādi ir daži projektēšanas mērķi, veidojot spēcīgus šifrus?
A: Kad cilvēki rada spēcīgus šifrus, viņi cenšas tajos iestrādāt labu lavīnas efektu, izmantojot tādus matemātiskus principus kā tauriņa efekts. Tāpēc lielākā daļa blokķīferu ir produktu šifri un tāpēc šifrēšanas funkcijām ir lieli datu bloki.
J: Kas notiek, ja algoritms neatbilst lavīnas efektam?
A: Ja algoritms lielā mērā neatbilst lavīnas efektam, tad tam ir slikta randomizācija, un to var daļēji vai pilnībā uzlauzt (uzlauzt) kriptoanalītiķi, kuri var veikt prognozes par ievadi, pamatojoties tikai uz doto izvadi.
J: Kāpēc lielākajā daļā blokķīferu izmanto produktu šifrus?
A: Lielākajā daļā blokķīferu izmanto produktu šifrus, jo tie palīdz tajos iestrādāt labu avalances efektu, izmantojot tādus matemātiskus principus kā tauriņa efekts.
J: Kāpēc hash funkcijām ir lieli datu bloki?
A: Šifrēšanas funkcijām ir lieli datu bloki, jo tas palīdz tajās iestrādāt labu avalances efektu, izmantojot tādus matemātiskus principus kā tauriņa efekts.
Meklēt