Matemātiskā zīme: pozitīvi un negatīvi skaitļi, zīmju nozīme
Uzzini par matemātiskajām zīmēm: pozitīvi un negatīvi skaitļi, nulles bezzīmīgums, plusa un mīnusa loma un skaitļu darbības — skaidrojumi ar saprotamiem piemēriem.
Matemātikā vārds "zīme" apzīmē īpašību būt pozitīvam vai negatīvam. Katrs reālais skaitlis (izņemot nulli) ir vai nu pozitīvs, vai negatīvs, un tāpēc tam ir zīme. Nulle pati par sevi ir bez zīmes jeb bezzīmju skaitlis. Parasti, ja skaitļus redz bez zīmes, tos uzskata par pozitīviem skaitļiem.
Kas nozīmē “pozitīvs” un “negatīvs”?
Pozitīvs skaitlis ir lielāks par nulli, un tam parasti raksta plusa zīmi vai raksta zīmi vispār nerakstot (piem., 3 vai +3). Negatīvs skaitlis ir mazāks par nulli, tam parasti raksta mīnusa zīmi (piem., -5). Zīme nosaka skaitļa virzienu uz skaitļu līnijas: pozitīvie atrodas pa labi no nulles, negatīvie — pa kreisi.
Zīmju darbības un pamatlikumi
Vēl viena bieži lietota zīmju jēdziena nozīme ir saistīta ar darbībām ar skaitļiem. Daži svarīgākie likumi:
- Saskaitīšana un atņemšana: pievienojot skaitļus ar vienādām zīmēm, saskaita to absolūtās vērtības (moduļus) un atstāj zīmi. Piemēram, (-3) + (-2) = -5. Ja zīmes atšķiras, atņem mazāko moduļa vērtību no lielākā un pieņem lielākā skaitļa zīmi.
- Reizināšana: zīmes reizina pēc vienkārša noteikuma:
- + × + = +
- + × - = -
- - × + = -
- - × - = +
- Dalīšana: seko tādiem pašiem principiem kā reizināšana attiecībā uz zīmēm: dalījuma zīme ir +, ja dalāmā un dalītāja zīmes ir vienādas, un - — ja atšķiras.
- Dubultais mīnuss: mīnuss priekšā mīnusam atceļ zīmes efektu: -(-a) = a.
Absolūtā vērtība un zīmes funkcija
Skaitļa absolūtā vērtība jeb modulis ir tā attālums no nulles, neatkarīgi no zīmes. Apzīmē ar |a|; piemēram, |−3| = 3 un |3| = 3.
Zīmes funkcija (bieži apzīmēta sgn(x)) parāda, vai skaitlis ir pozitīvs, negatīvs vai nulle:
sgn(x) = 1, ja x > 0; sgn(x) = 0, ja x = 0; sgn(x) = −1, ja x < 0.
Citi zīmju izmantojumi matemātikā
Vārdu zīme lieto arī plašākā matemātikas kontekstā, piemēram, lai apzīmētu simbolus (piem., plusa un mīnusa zīmes, reizināšanas zīmi) vai objektu daļas, kas var būt “pozitīvas” vai “negatīvas” attiecībā uz kādu īpašību. Dažās teorijās lieto zīmi, lai raksturotu vektoru komponentu virzienu, matricas īpašības vai funkciju vērtību zīmi.
Praktiski padomi
- Skaitļi bieži tiek uzrakstīti bez plusa zīmes; tas pašlaik nozīmē, ka tie ir pozitīvi.
- Rūpējieties, lasot izteiksmes ar daudzām zīmēm: -3^2 nav tas pats kas (-3)^2; eksponentālais darbības prioritāte ietekmē rezultātu.
- Matemātikā zīme palīdz saprast skaitļu uzvedību un būtiski atvieglo darbības ar algebraiskām izteiksmēm.
Dažkārt vārdu zīme lieto arī, lai apzīmētu dažādas matemātiskas zīmes, piemēram, plusa un mīnusa zīmes un reizināšanas zīmi.

Plus un mīnus simboli tiek izmantoti, lai parādītu skaitļa zīmi. Plus nozīmē pozitīvu, bet mīnus - negatīvu.
Skaitļa zīme
Par reālo skaitli saka, ka tas ir pozitīvs, ja tas ir lielāks par nulli, un negatīvs, ja tas ir mazāks par nulli. Pozitīvās vai negatīvās īpašības pazīmi sauc par skaitļa zīmi. Pašu nulli neuzskata par skaitli ar zīmi.
Aritmētikā skaitļa zīmi bieži apzīmē, pirms skaitļa liekot plusa vai mīnusa zīmi. Piemēram, +3 apzīmē pozitīvu skaitli 3, bet -3 apzīmē negatīvu skaitli 3. Ja plusa vai mīnusa zīme nav norādīta, galvenais veids, kā to saprast, ir tāds, ka skaitlis ir pozitīvs.
Jebkura skaitļa, kas nav nulle, zīmi var mainīt uz pozitīvu, izmantojot absolūtās vērtības funkciju. Piemēram, skaitļa -3 absolūtā vērtība un skaitļa 3 absolūtā vērtība ir vienādas ar 3. Simbolos tas būtu rakstāms |-3| = 3 un |3| = 3.
Nulles zīme
Skaitlis nulle nav ne pozitīvs, ne negatīvs, tāpēc tam nav zīmes. Aritmētiskā izteiksmē +0 un -0 abi apzīmē vienu un to pašu skaitli 0.
Zīmju nozīmes
Tā kā nulle nav nedz pozitīva, nedz negatīva, dažkārt nezināma skaitļa zīmes apzīmēšanai izmanto šādus apzīmējumus:
- Skaitlis ir pozitīvs, ja tas ir lielāks par nulli.
- Skaitlis ir negatīvs, ja tas ir mazāks par nulli.
- Skaitlis ir nenegatīvs, ja tas ir lielāks vai vienāds ar nulli.
- Skaitlis ir nepozitīvs, ja tas ir mazāks vai vienāds ar nulli.
Tādējādi nenegatīvs skaitlis ir vai nu pozitīvs, vai nulle, bet nepozitīvs skaitlis ir vai nu negatīvs, vai nulle. Piemēram, reālā skaitļa absolūtā vērtība vienmēr nav negatīva, bet ne vienmēr ir pozitīva.
Šo pašu definīciju dažkārt izmanto funkcijām, kas pieņem reālas vai veselu skaitļu vērtības. Piemēram, funkciju sauc par pozitīvu, ja visas tās vērtības ir pozitīvas, vai par nenegatīvu, ja visas tās vērtības nav negatīvas.
Leņķa zīme
Daudzos tekstos zīme ir bieži sastopama kopā ar leņķa mērījumu, jo īpaši leņķi, kas atrodas vai rotācijas leņķi. Šādā situācijā zīme norāda, vai leņķis ir pulksteņrādītāja rādītāja virzienā vai pretēji pulksteņrādītāja virzienam. Lai gan var izmantot dažādas konvencijas, matemātikā ir ierasts, ka leņķi pretēji pulksteņrādītāja virzienam tiek uzskatīti par pozitīviem, bet leņķi pulksteņrādītāja virzienā - par negatīviem.
Ir iespējams arī pievienot zīmi pagrieziena leņķim trīs dimensijās, pieņemot, ka pagrieziena ass ir orientēta. Precīzāk, pagrieziens pa labi ap asi parasti tiek uzskatīts par pozitīvu, bet pagrieziens pa kreisi - par negatīvu.
Virziena zīme
Aritmētikā un fizikā ir pieņemts noteiktus virzienus apzīmēt kā pozitīvus vai negatīvus. Pamata piemērs: skaitļu līnija parasti tiek zīmēta ar pozitīviem skaitļiem pa labi un negatīviem pa kreisi:
![]()
Dekarta plaknē virzienus pa labi un uz augšu parasti uzskata par pozitīviem - virziens pa labi ir pozitīvs x virziens, bet virziens uz augšu ir pozitīvs y virziens.
Citas nozīmes
Papildus reālā skaitļa zīmei vārdu zīme lieto arī dažādos ar to saistītos veidos matemātikā un dabaszinātnēs:
- Grafu teorijā ar zīmi apzīmēts grafs ir grafs, kurā katra mala ir apzīmēta ar pozitīvu vai negatīvu zīmi.
- Fizikā jebkuram elektriskajam lādiņam ir zīme - pozitīvs vai negatīvs. Saskaņā ar vispārīgiem noteikumiem pozitīvs lādiņš ir lādiņš ar tādu pašu zīmi kā protonam, bet negatīvs lādiņš ir lādiņš ar tādu pašu zīmi kā elektronam.
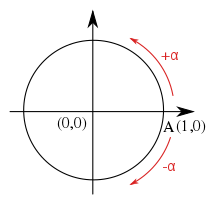
Mērot no ass x, leņķi uz vienības apļa skaitās pozitīvi pretēji pulksteņrādītāja virzienam un negatīvi pulksteņrādītāja virziena virzienā.
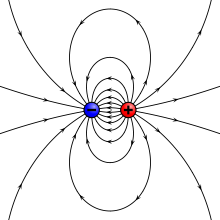
Elektriskais lādiņš var būt pozitīvs vai negatīvs.
Meklēt