Venn diagramma: definīcija, piemēri un pielietojums

Uzzini Venn diagrammas definīciju, skaidrus piemērus un praktisku pielietojumu loģikā, statistikā, lingvistikā un datorzinātnē — viegli saprotami un ilustrēti.

Venna diagramma ir diagramma, kas vizuāli parāda loģisko saistību starp kopām. To 1880. gados popularizēja Džons Venns, un mūsdienās Venna diagrammas tiek plaši izmantotas gan mācībās, gan praksē. Parasti kopas attēlo ar slēgtām līknēm uz plaknes — visbiežāk ar apļiem vai elipsēm — un visas kopas kopā parasti iezīmē universu (visu aplūkoto elementu kopu). Diagrammas palīdz saprast, kā kopas pārklājas, kuras daļas ir kopīgas un kuras — unikālas katrai kopai.

Venna diagrammas praktiski lieto, lai mācītu elementāru kopu teoriju un ilustrētu attiecības varbūtības, loģikas, statistikas, lingvistikas un datorzinātnes jomā. Vispārēji tās noder, ja nepieciešams skaidri parādīt saskares (intersektējošās) daļas, vienības vai atšķirības starp kopām.

Īsa vēsture

Līdzīgas idejas par diagrammatisku kopu attēlojumu parādījās jau agrāk nekā Vennam: Kristians Veise 1712. gadā (Nucleus Logicoe Wiesianoe) un Leonhards Eulers 1768. gadā (Vēstules vācu princesei) aprakstīja vai izmantoja līdzīgas vizuālās metodes. Tomēr Džons Venns 19. gadsimta beigās sistemātiski attīstīja un popularizēja šo pieeju savā darbā "Symbolic Logic" (1881), kurā iezīmēja to, ko mēs šodien pazīstam kā Venna diagrammas.

Kā lasīt Venna diagrammu — pamatjēdzieni

• Universums (U): parasti tiek attēlots kā taisnstūris ap visu diagrammu; tajā ietilpst visi aplūkotie elementi.
• Kopas: attēlotas kā slēgtas līnijas (apļi/elipses). Katra kopas iekšiene satur tās elementus.
• Saskare (A ∩ B): daļa, kur divu (vai vairāku) kopu apļi pārklājas — elementi, kas pieder visām iesaistītajām kopām.
• Vienība (A ∪ B): apgabals, kas ietver elementus, kas pieder vismaz vienai no kopām.
• Atšķirība (A \ B): elementi, kas pieder kopai A, bet nepieder kopai B.
• Kopas papildinājums (Aᶜ): visi universa elementi, kas nepieder kopai A.

Vienkārši piemēri

1) Divu kopu piemērs.

Pieņemsim, ka universums U = {1,2,3,4,5,6}, A = {1,2,3,4} un B = {3,4,5,6}. Venna diagrammā redzēsim:

• A ∩ B = {3,4} (pārklāšanās daļa)
• A ∪ B = {1,2,3,4,5,6} (kopējie elementi)
• A \ B = {1,2} un B \ A = {5,6}

2) Trīs kopu piemērs.

Trīs apļu Venna diagramma ļauj attēlot visas iespējamās daļas (kopumā 8 reģioni: katra no trim individuālajām daļām, trīs pāru saskares un viena trīspušu saskare, plus ārējais papildinājums). Šāda diagramma bieži tiek izmantota, lai visualizētu sarežģītākas attiecības, piemēram, trīs nosacījumu pārklāšanos varbūtības uzdevumos.

Bieži lietotie veidi un marķējumi

• Reģionu var apzīmēt ar skaitļiem vai burtu kombinācijām, lai vieglāk atsaukties (piem., reģions, kas pieder tikai A — “A tikai”).
• Reģionus var apzīmēt arī ar nosacījumiem vai procentiem, piemēram, “30% klientu pieder gan grupai A, gan B”.
• Diagrammas var nokrāsot vai ēnot, lai izceltu konkrētas daļas (piem., tikai saskari vai tikai papildinājumu).

Pielietojums praksē

• Mācību procesā — skaidro loģikas un kopu teorijas pamatus.
• Varbūtības un statistikas uzdevumos — izskaidro notikumu saskari un nosacītās varbūtības.
• Loģikā — parāda formulei atbilstošas reģionu saturs.
• Datorzinātnē — izmanto, lai modelētu datu kopu pārklāšanos, datu bāzu vaicājumus, kolēģialitātes analīzi u.c.
• Lingvistikas un statistikas pētījumos — analizē funkciju/sociolingvistisko kopu pārklāšanos.

Praktiski padomi un ierobežojumi

• Venna diagrammas ir ļoti noderīgas, ja kopas skaits ir neliels (parasti līdz 3–4 kopām). Ar vairākām kopām diagramma kļūst sarežģīta un grūti salasāma.
• Dažreiz labāk izmantot citas vizualizācijas metodes (tabulas, matricas, interaktīvus grafikus) lieliem datu kopumiem vai daudzām kopām.
• Ir svarīgi atšķirt Venna diagrammas no Euler diagrammām: Euler diagrammas nerāda visus iespējamos reģionus, tikai tos, kas satur reālus elementus, kamēr Venna diagrammas parāda visus teorētiski iespējamos pārklāšanās reģionus.

Venna diagrammas ir vienkāršs un efektīvs vizuālais līdzeklis, kas palīdz skaidrot un analizēt kopu attiecības. Tās ir viegli saprotamas, pielāgojamas un plaši izmantojamas gan izglītībā, gan pētījumos un praksē.

Piemērs

Šajā piemērā ir izmantotas divas kopas A un B, kas šeit attēlotas kā krāsaini apļi. Oranžais aplis, kopa A, apzīmē visas dzīvās radības, kas ir divkājainas. Zilais aplis, kopa B, attēlo dzīvās radības, kas var lidot. Katru atsevišķo radības veidu var iztēloties kā punktu kaut kur diagrammā. Dzīvās radības, kas var gan lidot, gan tām ir divas kājas, piemēram, papagaiļi, ir abās kopās, tāpēc tās atbilst punktiem apgabalā, kur zilais un oranžais aplis pārklājas. Šajā apgabalā ir visas šādas un tikai šādas dzīvās radības.

Cilvēki un pingvīni ir divkāji, tāpēc tie ir oranžajā aplī, bet, tā kā viņi nevar lidot, tie parādās oranžā apļa kreisajā daļā, kur tas nepārklājas ar zilo apli. Komāriem ir sešas kājas, un tie lido, tāpēc komāru punkts atrodas zilā apļa daļā, kas nepārklājas ar oranžo apli. Radības, kas nav divkājainas un nespēj lidot (piemēram, vaļi un zirnekļi), tiktu attēlotas ar punktiem ārpus abiem apļiem.

A un B kopu apvienoto apgabalu sauc par A un B apvienību, ko apzīmē ar A ∪ B. Šajā gadījumā apvienība ietver visas dzīvās radības, kas ir vai nu divkājainas, vai spēj lidot (vai abas). A un B apgabalu, kurā abas kopas pārklājas, sauc par A un B krustpunktu, ko apzīmē ar A ∩ B. Piemēram, abu kopu krustpunkts nav tukšs, jo ir punkti, kas attēlo radības, kuras atrodas gan oranžajā, gan zilajā aplisā.

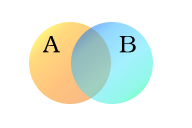
A (divkājainas radības) un B (lidojošas radības) komplekti.

Jautājumi un atbildes

J: Kas ir Venna diagramma?

J: Kas popularizēja Venna diagrammas?

J: Kādam nolūkam tās izmanto?

J: Kurš pirms Džona Vena ierosināja līdzīgas idejas?

J: Kad Džons Venns publicēja Simbolisko loģiku?

J: Kurā nodaļā "Simboliskajā loģikā" Džons Venns popularizēja Venna diagrammas ideju?

K: Kā šīs idejas tika attēlotas pirms V enna diagrammas mūsdienu versijas izgudrošanas?

Meklēt pēc burta