Pretestība un impedanse: definīcija, vienības un formulas

Pretestība un impedanse: skaidras definīcijas, vienības (Ω) un svarīgākās formulas (V=R·I, Z=j2πfL, Z=1/(j2πfC)) saprotami un praktiski.

Autors: Leandro Alegsa

02-01-2026 21:07

Elektriskā pretestība (rezistance) un impedanse ir saistīti, bet tomēr atšķirīgi jēdzieni, kas raksturo, kā komponenti vai ķēdes pretojas elektriskai strāvai. Strāvas un sprieguma izmaiņu (īpaši sinusoidālu) gadījumā jāņem vērā gan enerģijas izkliede, gan enerģijas uzkrāšana un atdošana — to visu sedz impedanse.

Definīcija un pamatforma

Rezistors pretojas cauri plūstošai strāvai neatkarīgi no frekvences (līdz pirmspārbūves robežām) — šī pretestība parasti apzīmēta ar R un raksturo to, cik liels spriegums V nepieciešams, lai nodrošinātu strāvu I:

V = R * I $V=R*I$

Impedanse Z ir vispārīgāka pretestības forma, kas ietver gan reālo daļu (R), gan iedomāto daļu (reaktanci X). Kompleksā (rektangulārā) formā to uzraksta kā:

Z = R + jX

piemēram, Z = 1 + 1 j {\displaystyle Z=1+1+1j} $Z=1+1j$

Otrais bieži izmantotais pieraksts ir polārā forma — lielums (absolūta vērtība) un fāze:

|Z| un ∠θ $\left\vert Z\right\vert$ $\angle \theta$

Pāreja no rektangulārās uz polāro formu: |Z| = sqrt(R² + X²), leņķis φ = atan2(X, R). Piemērs: Z = 1 + j1 ≈ 1,414 ∠ 45° (attēlā redzams kā Z = 1,4 ∠ 45°) $Z=1.4\angle 45^{\circ }$ .

Induktori un kondensatori — frekvences atkarība

Atšķirība starp vienkāršu rezistoru un impedansi ir tā, ka impedanse var mainīties atkarībā no frekvences (izmaiņu ātruma). Elektriskie komponenti reaģē uz frekvenci šādi:

Induktors pretojas strāvas izmaiņām — tā impulsora impedanse ir proporcionāla frekvencei: Z_L = jωL, kur ω = 2πf. (Oriģinālais pieraksts: Z = j 2 π f L {\displaystyle Z=j2\pi fL\,} $Z=j2\pi fL\,$
Kondensators pretojas sprieguma izmaiņām — tā impedanse samazinās ar frekvenci: Z_C = 1/(jωC). (Oriģinālais pieraksts: Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2\pi fC}}}} $Z={\frac {1}{j2\pi fC}}$

Te j apzīmē iedomāto vienību i (inženierijā biežāk lieto j, lai neizjauktu ar strāvas I), π ir pi, f — frekvence, L — induktivitāte, C — kapacitāte.

No šiem izriet arī reaktances (X) zīmes: X_L = +ωL (pozitīva), X_C = −1/(ωC) (negatīva). Pie f = 0 (līdzstrāva) Z_L = 0 (īssavienojums), Z_C → ∞ (atvērts ķēdes elements).

Sērijas un paralēlie savienojumi, kombinēšana

Impedanses kombinējas tāpat kā reālas pretestības, taču jālieto kompleksie skaitļi:

Sērijā: Z_total = Z1 + Z2 + ...
Paralēli: 1/Z_total = 1/Z1 + 1/Z2 + ... vai Z_total = (Z1·Z2)/(Z1+Z2) divu elementu gadījumā.

Šīs formulas ļauj aprēķināt, piemēram, rezonances frekvenci LC ķēdei: ω0 = 1/√(LC). Rezonanses punktā XL = −XC un ķēde uzvedas kā tīri reāla pretestība (ja nav citu zudumu).

Jauda, enerģija un reaktīvā darbība

Atšķirība starp rezistoru un reaģējošu elementu (induktors/kondensators) ir enerģijas izturēšana:

Rezistors izkliedē enerģiju siltumā — tā ir reālā jauda (P = V·I·cosφ).
Induktori un kondensatori uzkrāj un atdod enerģiju (reaktīvā jauda), tādēļ tie netērē enerģiju ilgtermiņā, bet ietekmē sprieguma un strāvas fāzi.

Atstarošana un saderība

Ja avota un slodzes (vai kabeļa) impedanses nav sakritīgi, daļa signāla tiek atstarota atpakaļ uz avotu. Atstarošanas koeficients apraksta šo attiecību:

Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}}} $\Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}$

kur Γ ir atstarošanas koeficients, Z_S ir avota (sīkāk: sūtītāja) impedanse un Z_L — slodzes impedanse. Lai nodrošinātu maksimālu jaudas pārvadi, bieži izmanto kompleksās konjugātās saderības principu: Z_S* = Z_L.

Viļņu pretestība (raksturīgā impedanse)

Jebkurai videi, kurā var izplatīties vilnis, ir sava raksturīgā impedance. Piemēram, tukšā telpa (brīvā telpa) kā vide elektromagnētiskam vilnim ir ar raksturīgo impedansi aptuveni 377 Ω $\Omega$

Praktiski piemēri un pielietojums

Audio un RF apakšsistēmās svarīgi pielāgot impedanses (piem., 50 Ω RF sistēmās), lai izvairītos no atspoguļojumiem.
Filtri (zemfrekvences, augstfrekvences, joslas) tiek projektēti, izmantojot inducētās un kapacitīvās impedanses, to frekvenču atkarību.
Transformators, motora tinums un rezonanses ķēdes izmanto induktivitātes un kapacitātes īpašības signālu formēšanā un enerģijas pārnešanā.

Kopsavilkums

Rezistence (R) — reāla pretestība, neatkarīga no fāzes, izkliedē enerģiju.
Impedanse (Z) — kompleksa pretestība, kas ietver reakciju uz mainīgu signālu (R + jX) un var atkaroties no frekvences.
Induktori un kondensatori rada reaktanci, kas mainās ar frekvenci; to impedanses sauc par Z_L = jωL un Z_C = 1/(jωC).
Vienības: omi (Ω), un inženierijā bieži lieto j iedomātajai vienībai, lai atšķirtu no strāvas I.

Ja nepieciešams, var pievienot vienkāršus aprēķinu piemērus (piem., pārvērst Z = 3 − j4 uz polāro formu, aprēķināt rezonanses frekvenci konkrētai L un C utt.), kā arī zīmējumus ar fāzes diagrammām un Bode diagrammām, lai labāk ilustrētu frekvenču ietekmi uz impedansi.

Signāls tiek daļēji atstarots atpakaļ, kur mainās pretestība.

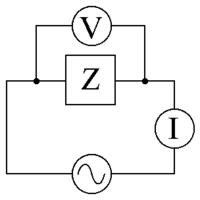
Maiņstrāvas avots, kas pievada spriegumu V {\displaystyle \scriptstyle V} $\scriptstyle V$ pāri pretestībai Z {\displaystyle \scriptstyle Z}. $\scriptstyle Z$ , kas rada strāvu I {\displaystyle \scriptstyle I} $\scriptstyle I$ .

Kompleksās impedances plaknes grafisks attēlojums

Fāze

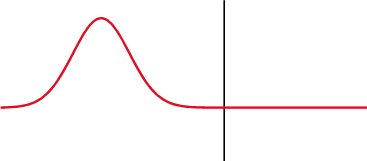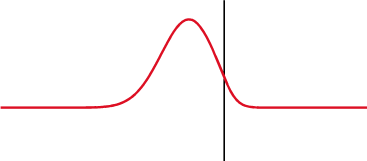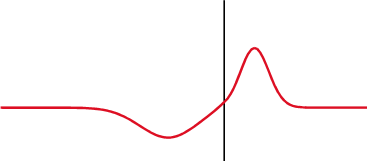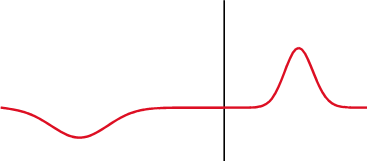
Caur rezistoru gan spriegums, gan strāva vienlaicīgi palielinās un samazinās, tiek uzskatīts, ka tie ir fāzē, bet ar pretestību ir citādi, spriegums ir nobīdīts par 1/4 viļņa garuma aiz strāvas kondensatorā un uz priekšu induktorā.

1/4 viļņa garumu parasti apzīmē ar iedomāto skaitli "j", kas arī atbilst 90 grādu nobīdei.

Iedomātā skaitļa "j" izmantošana padara matemātiku daudz vienkāršāku, tā ļauj aprēķināt kopējo pretestību tāpat, kā tas tiek darīts ar rezistoriem, piemēram, rezistors plus pretestība virknē ir R+Z, bet paralēli tā ir (R*Z)/(R+Z).

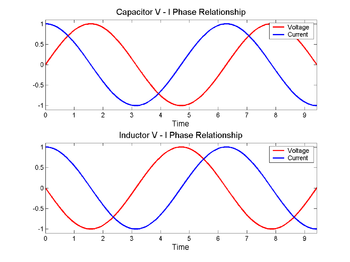
Kondensatorā (augšā) spriegums (sarkans) mainās pēc strāvas (zils), bet induktorā (apakšā) - pirms tam. Fāzes starpība starp spriegumu un strāvu ir 1/4 viļņa garuma.

Jautājumi un atbildes

J: Kas ir elektriskā pretestība?

A: Elektriskā pretestība ir pretestība, ko ķēde rada strāvas vai sprieguma izmaiņām.

J: Kā var rakstīt elektrisko pretestību?

A: Elektrisko pretestību var pierakstīt ar pretestību "R" (reālā daļa) un reaktanci "X" (iedomātā daļa), kā arī ar lielumu, fāzi, izmēru un leņķi.

J: Kāda ir atšķirība starp pretestību un impedanci?

A: Galvenā atšķirība starp pretestību un impedanci ir vārds "maiņa"; citiem vārdiem sakot, maiņas ātrums ietekmē pretestību. Pretestība pretojas jebkurai caur to plūstošai strāvai, kamēr induktors pretojas strāvas izmaiņām, bet kondensators pretojas sprieguma izmaiņām.

J: Kādas formulas ir saistītas ar pretestību un pretestību?

A: Attiecībā uz pretestību V=R*I, kur V ir spriegums, R ir pretestība un I ir strāva; attiecībā uz induktoriem Z=j2πfL; attiecībā uz kondensatoriem Z=1/j2πfC; kur Z ir pretestība, j ir iedomāts skaitlis -1 , π ir konstante pi, f ir frekvence, L ir induktivitāte, C ir kapacitāte.

J: Kādi ir daži fizikāli skaidrojumi pretestībai pret pretestību?

A: Pretestību rada elektronu sadursmes ar atomiem rezistoru iekšpusē, savukārt induktora pretestība rodas, radot elektrisko lauku, bet kondensatora pretestība rodas, radot magnētisko lauku. Turklāt rezistori izkliedē enerģiju, bet induktori un kondensatori uzkrāj enerģiju, ko pēc tam var atgriezt avotā, kad tā samazinās.

J: Kā aprēķināt atstarošanas koeficientu?

A: Atstarošanas koeficientu var aprēķināt, izmantojot Γ=(ZL-ZS)/(ZL+ZS), kur Γ (lielā gamma) ir atstarošanas koeficients; ZS ir avota pretestība; ZL ir slodzes pretestība.

Meklēt