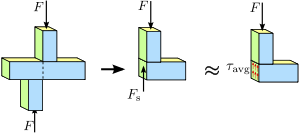Spriedze (mehāniskais spriegums): definīcija, formula un vienības
Spriedze (mehāniskais spriegums): definīcija, formula un vienības — skaidrojums par σ=F/A, SI vienību Pa (N/m²), imperiālo psi un sprieguma ietekmi uz materiālu.
Spriedze ir iekšējo spēku lielums uz laukuma vienību, kas iedarbojas uz ķermeņa daļiņām un izraisa tā formas maiņu. To var saprast arī kā spēku, ko viena ķermeņa daļiņa pielieto blakus esošajai daļiņai pāri iedomātai virsmai, kas tās atdala — tātad tas ir ķermeņa iekšējo spēku blīvums materiāla tilpumā. Šie iekšējie spēki parasti rodas kā reakcija uz ārējiem spēkiem (piem., nepārtrauktībā piemērojamiem virsmas vai ķermeņa spēkiem) un var izpausties kā saspiešana, izstiepšana vai slīdēšana materiālā.
Formula
Vienkāršākajā gadījumā, kad spēks ir vienmērīgi izkliedēts uz plaknes laukuma, normālsprieguma formula ir:
σ = F A {\displaystyle {\sigma }={\frac {F}{A}}}} 
kur σ ir spriegums, F ir spēks un A ir virsmas laukums. Pozitīva σ nozīmē stiepšanās (tension), negatīva — saspiešana (compression), ja lieto ierasto zīmju konvenciju.
Vienības
Starptautiskajā SI sistēmā spēku mēra ņūtonos, bet laukumu — kvadrātmetros. Tādējādi spriedze ir N/m2. Tomēr parastā SI mērvienība spriedzei ir paskāls (Pa):
- 1 Pa = 1 N/m2.
Ķīmijā un inženierzinātnēs bieži lieto arī lielākas vienības, piemēram, kilopaskālu (kPa), megapaskālu (MPa) vai gigapaskālu (GPa). Imperiālajās vienībās spriegumu mēra mārciņspēkā uz kvadrātcollu (psi). Spriedzes mērvienība ir tāda pati kā spiediena mērvienība.
Spriedzes veidi
- Normālspriegums (σ) — darbojas perpendikulāri šķērsgriezes plaknei; izstiepjošs vai saspiedošs.
- Šķērspriegums (τ) — darbojas paralēli šķērsgriezes plaknei un mēģina izraisīt slīdēšanu starp slāņiem.
Sprieguma apraksts nepārtrauktības mehānikā
Nepārtrauktības mehānikā deformējams ķermenis tiek modelēts kā nepārtrauktība, tāpēc iekšējie spēki sadalās materiāla tilpumā nepārtraukti. Tas nozīmē, ka sprieguma lauks ķermenī ir laika un telpas funkcija, ko var izteikt kā lauka vektoru vai tenzoru. Spēku iedarbība izraisa ķermeņa deformāciju; ja materiāls nav pietiekami izturīgs, deformācija var pāraugt pastāvīgā bojājumā vai plaisā.
Sprieguma tensori un galvenie spriegumi
Vispārīgākai sprieguma aprakstīšanai nepieciešams sprieguma tensora jēdziens — 3×3 matrica, kas satur gan normālos, gan šķērspriegumus kopā. No šī tensora var iegūt galvenos spriegumus (principal stresses), kas ir normālie spriegumi koordinātu sistēmā, kur šķērspriegumi izzūd. Galvenie spriegumi un to attiecības palīdz novērtēt materiāla lūzuma risku un piemērot attiecīgus izturības kritērijus (piem., von Mises, Tresca).
Praktiskais pielietojums un piemērs
Inženierijā sprieguma aprēķini nepieciešami, lai izvēlētos pareizu materiālu un šķērsgriezumu konstrukcijām (sijas, kolonnas, skrūves utt.), novērtētu drošības koeficientu un paredzētu deformācijas. Piemērs:
- Ja uz plakanu virsmu ar laukumu A = 0.02 m2 iedarbojas spēks F = 1000 N, tad σ = F/A = 1000 / 0.02 = 50 000 N/m2 = 50 kPa.
Modelēšana un ierobežojumi
Dažādi nepārtrauktības mehānikas modeļi pieņem atšķirīgas aproksimācijas par to, kā spēki un spriegumi sadalās materiālā. Klasiskajos modeļos lieto vidējo spēku pieņēmumu, bet sarežģītākos modeļos — jāņem vērā ģeometrijas ietekme, materiāla nelinearitāte un trīsdimensiju efekti. Ķermeņa ģeometrija var būt būtiska sprieguma koncentrāciju, plaisu attīstības un enerģijas uzkrāšanās ziņā, tāpēc praktiskos aprēķinos bieži izmanto galīgo elementu metodi (FEM).
Kopsavilkums
- Spriedze = spēks uz laukuma vienību; vienkāršā gadījumā σ = F/A.
- Vienība SI: paskāls (Pa) = N/m2.
- Spriedze var būt normāla vai šķērsgriezuma; reālām problēmām jāizmanto sprieguma tensora analīze un atbilstoši materiāla izturības kritēriji.
1.4. attēls Slīpes spriegums prizmatiskā stienī. Spriedzes vai spēka sadalījums stieņa šķērsgriezumā ne vienmēr ir vienmērīgs. Tomēr vidējais bīdes spriegums τ a v g {\displaystyle \tau _{\mathrm {avg} }\,\! }
ir saprātīga aproksimācija.
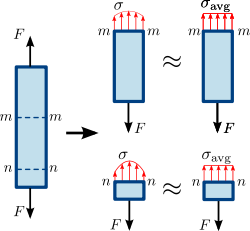
1.3. attēls Normālspriegums prizmatiskā (taisna vienāda šķērsgriezuma taisna elementa) stienī. Spriedzes vai spēka sadalījums stieņa šķērsgriezumā ne vienmēr ir vienmērīgs. Tomēr vidējais normālspriegums σ a v g {\displaystyle \sigma _{\mathrm {avg} }\,\! }
var izmantot.
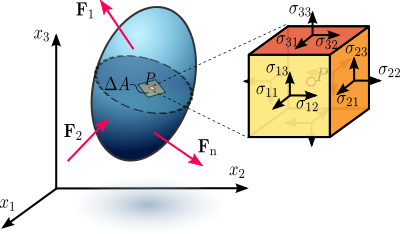
1.1. attēls Spriegums deformējamā materiālā ķermenī, kas pieņemts kā nepārtrauktība.
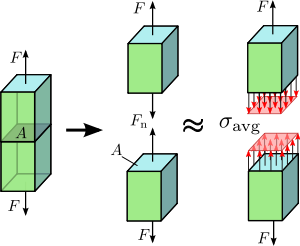
1.2. attēls Aksiāli noslogota prizmatiska stieņa aksiālais spriegums.
Šļauces spriegums
Papildu informācija: Šļauces spriegums
Vienkārši spriegumi
Dažās situācijās spriegumu objektā var aprakstīt ar vienu skaitli vai vienu vektoru (skaitli un virzienu). Trīs šādas vienkāršas stresa situācijas ir vienass normālais spriegums, vienkāršais bīdes spriegums un izotropais normālais spriegums.
Vienass normālais spriegums
Stiepes spriegums (vai stiepes spriegums) ir sprieguma stāvoklis, kas izraisa izplešanos; tas nozīmē, ka materiāla garumam ir tendence palielināties stiepes virzienā. Materiāla tilpums paliek nemainīgs. Ja uz ķermeni iedarbojas vienādi un pretēji spēki, tad šī spēka radīto spriegumu sauc par stiepes spriegumu.
Tāpēc vienass materiālā garums palielinās stiepes sprieguma virzienā, bet pārējos divos virzienos samazinās. Vienass stiepes veidā stiepes spriegumu rada vilkšanas spēki. Stiepes spriegums ir pretējs spiedes spriegumam.
Tieša spriegojuma konstrukcijas elementi ir troses, grunts enkuri un naglas, bultskrūves utt. Sijas, kas pakļautas lieces momentiem, var būt pakļautas gan stiepes spriegumam, gan spiedes spriegumam un/vai bīdes spriegumam.
Stiepes spriegumu var palielināt, līdz tiek sasniegta stiepes izturība, proti, sprieguma robežstāvoklis.
Spriedze viendimensiju ķermeņos
Visi reālie objekti aizņem trīsdimensiju telpu. Tomēr, ja divas dimensijas ir ļoti lielas vai ļoti mazas salīdzinājumā ar citām, objektu var modelēt kā viendimensiju. Tas vienkāršo objekta matemātisko modelēšanu. Pie viendimensiju objektiem pieder stieples gabals, kas noslogots galos un skatīts no malas, un metāla loksne, kas noslogota uz priekšējās puses un skatīta tuvumā un šķērsgriezumā.
Saistītās lapas
- Spriegums
- Liekšana
Jautājumi un atbildes
J: Kas ir stress?
A: Spriedze ir spēks uz laukuma vienību, kas iedarbojas uz ķermeni un izraisa tā formas maiņu. Tas ir ķermeņa iekšējo spēku mērs starp tā daļiņām, un tas ir vidējais spēks uz laukuma vienību, ko ķermeņa daļiņa iedarbojas uz blakus esošajām daļiņām pāri iedomātai virsmai, kas tās atdala.
J: Kā ārējie spēki ietekmē spriegumu?
A: Ārējie spēki ir vai nu virsmas spēki, vai ķermeņa spēki, un tie izraisa ķermeņa formas deformāciju, kas var novest pie pastāvīgas formas maiņas vai struktūras sabrukuma, ja materiāls nav pietiekami izturīgs.
J: Kāda ir vienass normālsprieguma formula?
A: Vienass normālsprieguma formula ir σ = F/A, kur σ ir spriegums, F ir spēks un A ir virsmas laukums. SI vienībās spēku mēra ņūtonos, bet laukumu - kvadrātmetros, tātad spriegums būtu ņūtons uz kvadrātmetru (N/m2). Tomēr pastāv sava SI vienība, ko sauc par paskālu (Pa) un kas ir vienāds ar 1 N/m2. Imperiālajās vienībās to mērītu mārciņspēkā uz kvadrātcollu (psi).
J: Ko nepārtrauktības mehānika pieņem par spēku?
A: Klasiskajos nepārtrauktās mehānikas modeļos pieņem vidējo spēku un pienācīgi neiekļauj ģeometriskos faktorus, t. i., neņem vērā to, kā ģeometrija ietekmē enerģijas uzkrāšanos ārējā spēka iedarbības laikā.
J: Kā dažādi modeļi var dot atšķirīgus rezultātus, aplūkojot matērijas un cietu ķermeņu deformāciju?
A: Dažādi modeļi atšķirīgi aplūko matērijas un cietu ķermeņu deformāciju, jo matērijas un cietu ķermeņu īpašības ir trīsdimensiju - tāpēc katrā pieejā tiek ņemti vērā dažādi aspekti, kas var dot atšķirīgus rezultātus.
J: Kā nepārtrauktības mehānikā aplūko deformējamus ķermeņus ar slodzi?
A: Nepārtrauktības mehānikā deformējami ķermeņi tiek uzskatīti par nepārtrauktiem ķermeņiem - tas nozīmē, ka iekšējie spēki ir vienmērīgi sadalīti materiālā ķermeņa tilpumā, nevis koncentrēti noteiktos punktos, kā tas ir klasiskajos modeļos.
Meklēt