Magnētiskais moments: definīcija, magnētiskais dipols un pielietojumi
Uzzini par magnētisko momentu, magnētisko dipolu un to pielietojumiem — teorija, piemēri un praktiskie risinājumi elektronikā, fizikā un inženierijā.
Magnēta magnētiskais moments ir lielums, kas nosaka spēku, ar kādu magnēts var iedarboties uz elektrisko strāvu, un griezes momentu, ar kādu magnētu ietekmē magnētiskais lauks. Elektriskās strāvas cilpai, stieņa magnētam, elektronam, molekulai un planētai ir magnētiskie momenti. Gan magnētisko momentu, gan magnētisko lauku var uzskatīt par vektoriem ar lielumu un virzienu. Magnētiskā momenta virziens ir no magnēta dienvidu pret ziemeļu polu. Magnēta radītais magnētiskais lauks arī ir proporcionāls tā magnētiskajam momentam. Precīzāk, termins "magnētiskais moments" parasti attiecas uz sistēmas magnētisko dipola momentu, kas rada pirmo locekli vispārējā magnētiskā lauka daudzpolu izvērsumā. Objekta magnētiskā lauka dipoliskā komponente ir simetriska attiecībā pret tā magnētiskā dipoliskā momenta virzienu un samazinās kā apgrieztais kubs attālumam no objekta.
Kas ir magnētiskais dipols un kā to attēlo
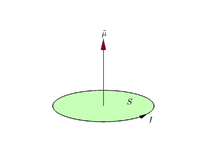
Magnētiskais dipols ir vienkāršākais magnētiskās konfigurācijas modelis — tas atgādina mazu strāvas cilpu vai mazu stieni ar ziemeļu un dienvidu poli. To apraksta magnētiskā dipola moments μ (bulta ar virzienu un lielumu). Praksē droši lieto divus izteiksmes veidus:
- Strāvas cilpai: μ = I·A (vektoriāli μ = I·A·n), kur I ir strāva, A — cilpas laukums un n — normālvektors, kurš nosaka μ virzienu (labās rokas likums: īkšķis norāda μ, pirksti — strāvas virzienu).
- Kvantu sistēmās, piemēram, elektronam, magnētiskais moments saistīts ar orbītālo momentu un spinu; atsevišķiem gadījumiem izmanto Bohr magnētona μB kā mērvienību.
Galvenās formulas un fizikālās īpašības
- Griezes moments strādājot laukā: τ = μ × B — magnētiskais moments mēģinās orientēties paralēli magnētiskajam laukam.
- Potenciālā enerģija magnētiskā laukā: U = −μ · B — tā nosaka, cik stabila ir dipola orientācija laukā.
- Attāluma atkarība laukam dipolā: attālajā zonā magnētiskais lauks B(r) no dipola samazinās kā 1/r^3. Precīzāk SI formā: B(r) = (μ0/4πr^3)[3(μ·r̂)r̂ − μ], kur μ0 ir vakuuma magnētiskā permeabilitāte.
- SI vienība magnētiskajam momentam ir ampēri reizi kvadrātmetrs (A·m2).
Magnētiskā momenta izcelsme mikroskopiskā līmenī
Atomos un molekulās magnētiskie momenti rodas no elektronkuģības (orbītālās kustības) un elektrona spina. Elektronu magnētiskais moments parasti izteikts caur Bohr magnētonu μB ≈ 9.274×10^−24 A·m^2. Daudzos materiālos atomu vai jonu magnētiskie momenti kopā veido makroskopisku spontānu vai inducētu magnētismu (piem., feromagnētismu, paramagnētismu, diamagnētismu).
Pielietojumi un nozīmīgums
- Kompass un orientēšanās: pamata princips, kur Zemes magnētiskais moments orientē kompasu adatu.
- Medicīna — magnētiskā rezonanse (MRI): magnētisko momentu saskaņošana laukā un to radiofrekvences reakcijas nodrošina attēlus cilvēka ķermenī.
- Informācijas glabāšana: cietie diski un magnētiskās lentes izmanto lokālus magnētiskos momentus, lai kodētu datus.
- Sensors un momentu mērīšana: torzijas momenta mērītāji, magnetometri (piem., SQUID) nosaka ļoti nelielus magnētiskos momentus.
- Fundamentālā fizika: elementārdaļiņu magnētiskie momenti (piem., elektrona dipola moments) ir svarīgi standarta modeļa pārbaudēm un jaunu fizikas parādību meklēšanai.
Praktiski piemēri
- Vienkārša strāvas cilpa: ja cilpai ar laukumu 0.01 m2 tek strāva 2 A, tad μ = I·A = 0.02 A·m2.
- Zemes magnētiskais moments: Zemei ir liels magnētiskais moments, kas nosaka globālo magnētisko lauku un kompasu darbību.
- Elektrona magnētiskais moments: kvantfizikā electrona spina magnētiskais moments nosaka daudzas atomu spektra īpašības un magnētiskos materiālus.
Secinājums
Magnētiskais moments, un jo īpaši magnētiskais dipola moments, ir centrāls jēdziens magnētismā — tas apraksta, kā objekts mijiedarbojas ar magnētisku lauku (griezes moments, potenciālā enerģija) un kādus laukus objekts rada apkārt. Izpratne par magnētiskajiem momentiem ir būtiska gan inženierijā un medicīnā, gan fundamentālajā fizikā.
Divas momenta definīcijas
Mācību grāmatās magnētisko momentu definēšanai izmanto divas savstarpēji papildinošas pieejas. Pirms 1930. gada mācību grāmatās tie tika definēti, izmantojot magnētiskos polus. Lielākajā daļā jaunāko mācību grāmatu tie definēti, izmantojot Ampera strāvu.
Magnētiskā pola definīcija
Fiziķi magnētisko momentu avotus materiālos attēlo kā polus. Ziemeļu un dienvidu polis ir analogs pozitīvajam un negatīvajam lādiņam elektrostatikā. Aplūkojiet stieņa magnētu, kuram ir vienāda lieluma, bet pretējas polaritātes magnētiskie poli. Katrs polis ir magnētiskā spēka avots, kas, palielinoties attālumam, pavājinās. Tā kā magnētiskie poli vienmēr ir pa pāriem, to spēki viens otru daļēji atsver, jo, kamēr viens pols velk, otrs atgrūž. Šī atcelšana ir vislielākā, ja poliem ir tuvu viens otram, t. i., ja stieņa magnēts ir īss. Tāpēc magnētiskais spēks, ko rada stieņa magnēts noteiktā telpas punktā, ir atkarīgs no diviem faktoriem: gan no tā polu stipruma p {\displaystyle p}
, gan no vektora l {\displaystyle \mathbf {l}. }, kas tos 
atdala. Moments ir definēts šādi
m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . } 
Tas norāda virzienu no dienvidiem uz ziemeļu polu. Analogiju ar elektriskiem dipoliem nevajadzētu uztvert pārāk tālu, jo magnētiskie dipoli ir saistīti ar leņķisko momentu (sk. Magnētiskais moments un leņķiskais moments). Tomēr magnētiskie dipoli ir ļoti noderīgi magnetostatiskajos aprēķinos, īpaši lietojumos ar feromagnētiem. Praktiķi, kas izmanto magnētisko polu pieeju, parasti attēlo magnētisko lauku ar irocionālo lauku H {\displaystyle \mathbf {H} } 
pēc analoģijas ar elektrisko lauku E {\displaystyle \mathbf {E}}. } 
.
Pašreizējās cilpas definīcija
Pieņemsim, ka pa plakanu slēgtu cilpu plūst elektriskā strāva I {\displaystyle I}
un tai ir vektora laukums S {\displaystyle \mathbf {S}. } 
( x {\displaystyle x}
, y {\displaystyle y} 
, un z {\displaystyle z} šā vektora 
koordinātes ir cilpas projekciju laukumi uz y z {\displaystyle yz}. 
, z x {\displaystyle zx}. 
un x y {\displaystyle xy} 
plaknēm). Tās magnētiskais moments m {\displaystyle \mathbf {m} } 
, vektors, ir definēts kā:
m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . } 
Saskaņā ar konvenciju vektora laukuma virzienu nosaka pēc labās rokas satvēriena noteikuma (labās rokas pirkstu izliekšana strāvas virzienā ap cilpu, kad plauksta "pieskaras" cilpas ārējai malai, un taisnais īkšķis norāda vektora laukuma un līdz ar to magnētiskā momenta virzienu).
Ja cilpa nav plakana, tad moments ir dots kā
m = I 2∫ r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . } 
Vispārīgākajā patvaļīga strāvas sadalījuma telpā gadījumā šāda sadalījuma magnētisko momentu var atrast no šāda vienādojuma:
m = 12∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,} 
kur r {\displaystyle \mathbf {r} }
ir pozīcijas vektors, kas vērsts no sākuma uz tilpuma elementa atrašanās vietu, un J {\displaystyle \mathbf {J} ir pozīcijas vektors, kas vērsts no sākuma uz tilpuma elementa atrašanās vietu, un J {\displaystyle \mathbf {J} }
ir strāvas blīvuma vektors šajā vietā.
Iepriekš minēto vienādojumu var izmantot, lai aprēķinātu jebkuras kustīgu lādiņu kopas, piemēram, rotējošas cietvielas ar lādiņu, magnētisko momentu, aizvietojot to ar
J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} , } 
kur ρ {\displaystyle \rho }
ir elektriskā lādiņa blīvums noteiktā punktā un v {\displaystyle \mathbf {v} } 
ir šī punkta momentānais lineārais ātrums.
Piemēram, magnētiskais moments, ko rada elektriskais lādiņš, kas pārvietojas pa apļveida ceļu, ir šāds.
m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v} } 
,
kur r {\displaystyle \mathbf {r} } ir lādiņa q {\displaystyle q}
stāvoklis attiecībā pret apļa centru un v {\displaystyle \mathbf {v} } ir lādiņa momentānais ātrums.
Praktiķi, kas izmanto strāvas cilpas modeli, parasti magnētisko lauku attēlo ar solenoidālo lauku B {\displaystyle \mathbf {B} } 
, kas ir analogs elektrostatiskajam laukam D {\displaystyle \mathbf {D}}. } 
.
Solenoīda magnētiskais moments
Iepriekš minētās strāvas cilpas vispārinājums ir daudzgriezienu spole jeb solenoīds. Tās moments ir atsevišķu vijumu momentu vektoru summa. Ja solenoīdam ir N {\displaystyle N} 
vienādu vijumu (vienslāņu tinums),
m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . } 
Solenoīda 3-D attēls.
Moments m {\displaystyle \mathbf {m} } plakana strāvas cilpa ar laukumu S {\displaystyle S}
un strāvu I {\displaystyle I} .
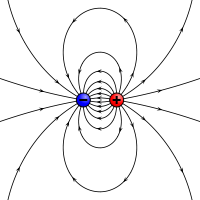
Elektrostatiskais analogs magnētiskajam momentam: divi pretēji lādiņi, kurus šķir galīgs attālums.
Vienības
Magnētiskā momenta mērvienība nav Starptautiskās mērvienību sistēmas (SI) pamatvienība, un to var attēlot vairāk nekā vienā veidā. Piemēram, strāvas cilpas definīcijā laukumu mēra kvadrātmetros un I {\displaystyle I} mēra ampēros, tāpēc magnētisko momentu mēra ampērmetros ( A m {\displaystyle2 {\text{A m}}^{2}}
). Vienādojumā par griezes momentu griezes momentu mēra ņūtonmetros, bet magnētisko lauku - teslās, tāpēc griezes momentu mēra N.m uz vienu teslu ( N.m T - 1{\displaystyle {\displaystyle {\text{N.m T}}^{-1}}
). Šie divi izteiksmes veidi ir līdzvērtīgi:
A m = 2N.m T - 1. {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. } 
CGS sistēmā ir vairākas dažādas elektromagnētisma vienību kopas, no kurām galvenās ir ESU, Gausa un EMU. Starp tām CGS sistēmā ir divas alternatīvas (neekvivalentas) magnētiskā dipola momenta vienības:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (m-A2 vai N.m/T)
un (biežāk izmantotais)
(EMU CGS un Gausa CGS) 1 erg/G = 1 abA-cm² = 10-3 (m-A2 vai N.m/T).
Šo divu neekvivalentu CGS vienību attiecība (EMU/ESU) ir precīzi vienāda ar gaismas ātrumu brīvā telpā, kas izteikts cm/s.
Visas formulas šajā rakstā ir pareizas SI mērvienībās, bet citās mērvienību sistēmās formulas var būt jāmaina. Piemēram, SI vienībās strāvas cilpai ar strāvu I un laukumu A ir magnētiskais moments I×A (sk. tālāk), bet Gausa vienībās magnētiskais moments ir I×A/c.
| Dažu elementārdaļiņu iekšējie magnētiskie momenti un spini | ||
| Daļiņas | Magnētiskais dipola moments SI vienībās (10 −27J/T) | Spina kvantu skaitlis (bez dimensijas) |
| -9284.764 | 1/2 | |
| protonu | 14.106067 | 1/2 |
| neitronu | -9.66236 | 1/2 |
| mionu | -44.904478 | 1/2 |
| deitēronu | 4.3307346 | 1 |
| triton | 15.046094 | 1/2 |
Saistību starp magnētiskā momenta un magnetizācijas jēdzieniem skatīt magnetizācija.
Jautājumi un atbildes
J: Kas ir magnēta magnētiskais moments?
A: Magnēta magnētiskais moments ir lielums, kas nosaka spēku, ar kādu magnēts var iedarboties uz elektrisko strāvu, un griezes momentu, ar kādu magnēts iedarbosies uz magnētisko lauku.
J: Kuriem objektiem ir magnētiskie momenti?
A: Magnētiskais moments piemīt elektriskās strāvas cilpai, stieņa magnētam, elektronam, molekulai un planētai.
J: Kā var ņemt vērā gan magnētisko momentu, gan magnētisko lauku?
A: Gan magnētisko momentu, gan magnētisko lauku var uzskatīt par vektoriem ar lielumu un virzienu.
J: Kurā virzienā ir magnēta magnētiskais moments?
A: Magnētiskā momenta virziens ir no magnēta dienvidu līdz ziemeļu poliem.
J: Kāda ir saistība starp magnēta magnētisko momentu un magnētisko lauku?
A: Magnēta radītais magnētiskais lauks ir proporcionāls tā magnētiskajam momentam.
J: Ko parasti apzīmē ar terminu magnētiskais moments?
O: Precīzāk, termins magnētiskais moments parasti attiecas uz sistēmas magnētisko dipola momentu, kas rada pirmo locekli vispārējā magnētiskā lauka daudzpolu izvērsumā.
J: Kā uzvedas objekta magnētiskā lauka dipola komponente, palielinoties attālumam no objekta?
A: Objekta magnētiskā lauka dipola komponente ir simetriska attiecībā pret tā magnētiskā dipola momenta virzienu, un tā samazinās kā apgrieztais kubs attālumam no objekta.
Meklēt